Computer Science 6743 -- Complexity of Computational Problems, Fall 2008

Announcements

Old announcements

Assignments and tests

Assignment 1. Due Oct 9, 2007.

Assignment 2. Due Oct 30, 2007.

Assignment 3. Due Nov 27, 2007.

For typesetting please use LaTeX. A good introduction to LaTeX is "Essential LaTeX" .

Lecture Notes

A brief list of topics and theorems for the midterm (review sheet).

• Lecture 1 (Sep 11): Introduction and Turing machines
• Lecture 2 (Sep 13): Turing machines, review of computability, complexity classes and reducibility
• Lecture 3 (Sep 18): Complexity classes and reducibility, hierarchy theorems
• Lecture 4 (Sep 20): Completeness, space vs. time, padding
• Lecture 5 (Sep 25): Examples for assignment, NP
• Lecture 6 (Sep 27): Nondeterministic complexity classes
• Lecture 7 (Oct 2): Satisfiability, examples of reductions
• Lecture 8 (Oct 4): Cooks and Fagins theorems
• Lecture 9 (Oct 11): NP as games, co-NP, proof complexity
• Lecture 10 (Oct 16): Examples of reductions: HamCycle, SubsetSum, Partition
• Lecture 11 (Oct 18): SubsetSum, 3Col, search-to-decision reductions, non-deterministic time hierarchy theorem.
• Lecture 12 (Oct 23): Savitch and Immerman-Szelepcsenyi theorems
• Lecture 13 (Oct 25): Discussing the assignment: no notes.
• Lecture 14 (Oct 30): PSPACE and PH
• Lecture 15 (Nov 1): Circuit complexity, P/poly, AC^0
• Lecture 16 (Nov 6): Review, Circuit complexity vs. time/space
• Midterm (Nov 8): no notes.
• Lecture 17 (Nov 13): Randomized computation
• Lecture 18 (Nov 15): Interactive protocols, counting classes
• Lecture 19 (Nov 20): IP=PSPACE, #SAT in IP, classes AM and MA
• Lecture 20 (Nov 22): Zero-knowledge proofs, PCP theorem, approximation algorithms and non-approximability
• Lecture 21 (Nov 27): Ladner's theorem and Schaefer's theorem

Course information Course Information Sheet Lectures: TBA Instructor: Antonina Kolokolova , email: [Your browser cannot view this email address] , office ER-6011. Textbook: M. Sipser: Introduction to the Theory of Computation (second edition). We will also use lecture notes from similar courses (to be posted later). Marking scheme (tentative!): 3 assignments 15% each, a midterm %15, a presentation 10%, and a final exam 30%. Description: The goal of this course is to help students develop an intuitive feel for hardness of computational problems, and an ability to prove that intuition. What does it mean that a given problem is "hard"? In which sense is it "hard": is it memory-intensive, computation-intensive; how are these notions related? How expressive are various languages used in databases and AI, and what does it mean computationally? These are some of the questions we will explore in this course. In particular, we will cover the classical P vs. NP problem (is checking a solution easier than finding a solution? Nobody knows!), as well as classes of higher complexity (polynomial-time hierarchy), space classes, counting classes, randomized and circuit complexity, and descriptive and proof complexity. We will also review some computability theory and, time permitting, cover a range of advanced topics such as PCP, natural proofs (why it is hard to resolve the P vs. NP question), hardness of approximation, etc.

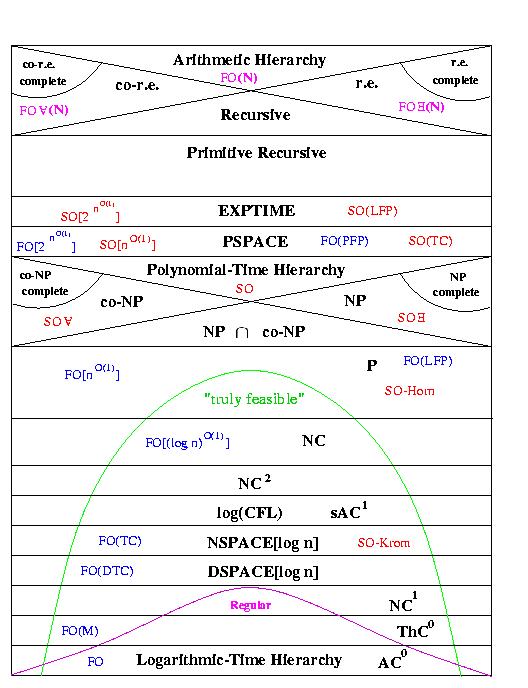(this picture is from the cover of the book "Descriptive Complexity" by Neil Immerman)