23/3/2015 Several classic papers, including Impagliazzo's "5 worlds" paper, are posted below in the lecture notes section.
- 17/3/2015 My office hour tomorrow will be 11am-12pm (I will not be able to make it at the usual time). If this time does not work for you and you would like to see me, please email and we will arrange some other time.
- 1/3/2015 Here is the brief study guide for the midterm exam on Wednesday. If you know this material, and can solve all problems on submitted assignments, you should have no problem with the exam.
- 22/2/2015 The due date for assignment 2 has been moved to Wed,Feb 25th, 11:59pm.
- 18/2/2015 Assignment 1 marks are now posted on D2L . Please email me if you have any questions.
- 17/2/2015 I should be in my office for office hours tomorrow, Wednesday Feb 18th, from 1 to 2pm. Please see me then if you have questions about the assignment 2, or email me if this time does not work.
- 12/2/2015 As we did not have time to cover the material for questions 3 and 4 of assignment 2, please only do questions 1 and 2. Here is the new pdf and here is the LaTeX source file . The due date remains Feb 23rd, please submit your pdf by 10pm on D2L.
- 11/2/2015 Reminder: there will be no lecture for the next two weeks (Feb 16th and 18th is the midterm break, and Feb 23 and 25 I am out of town). If you would like to talk about the assignment, please email me and set up an appointment before Feb 19th.
- 10/2/2015 A nice Youtube video explaining complexity theory and P vs. NP problem. Than you Sohel for finding it!
- 9/2/2015 Assignment 2 is now posted. Due Feb 23rd by 10pm on D2L. Please submit a pdf; here is the Latex source.
- Assignment 1 is now due Sunday, Feb 8th, at 10pm. Submit your .pdf compiled in LaTeX on D2L.
- 21/1/2015 Assignment 1 is now posted. Due Feb 4th.
- 19/1/2015 For undecidability, please see notes from my undergrad course .
- 19/1/2015 My office hours this week will be 11:30-12:30 on Wednesday, an hour earlier than usual.
- 6/1/2015 Notes for Lecture 1 are now posted below.
- 5/1/2015 There will be no classes on February 23 and 25. To make up for that, the next four Monday lectures (Jan 12,19,26 and Feb 2nd) will be extended till about 7:25pm.
For typesetting please use LaTeX. I will post source files for the assignments. A good, though outdated, introduction to LaTeX is
"Essential LaTeX" .
Lectures: 5:30-7pm Mondays and Wednesdays in EN-1051.
Instructor: Antonina
Kolokolova , email: [Your browser cannot view this email address]
, office ER-6033.
Instructor office hours: Wednesdays 12:30-1:30pm, or by appointment.
Textbook:
Computational Complexity: A Modern Approach by Sanjeev Arora and Boaz Barak.
The link is to the online version, containing an earlier draft of the book.
Reference book: M. Sipser:
Introduction to the Theory of Computation (second edition).
We will also use lecture notes from similar courses (to be posted later).
Marking scheme (tentative!): 3 assignments 15% each,
a midterm %20, and a final exam 35%.
Description:
The goal of this course is to help students develop an intuitive feel
for hardness of computational problems, and an ability to prove that
intuition. What does it mean that a given problem is "hard"? In which
sense is it "hard": is it memory-intensive, computation-intensive; how
are these notions related? How expressive are various languages used
in databases and AI, and what does it mean computationally? These are
some of the questions we will explore in this course.
In particular, we will cover the classical P vs. NP problem (is
checking a solution easier than finding a solution? Nobody knows!), as
well as classes of higher complexity (polynomial-time hierarchy),
space classes, counting classes, randomized and circuit complexity,
and descriptive and proof complexity. We will also review some
computability theory and, time permitting, cover a range of advanced
topics such as PCP, natural proofs (why it is hard to resolve the P
vs. NP question), hardness of approximation, etc.
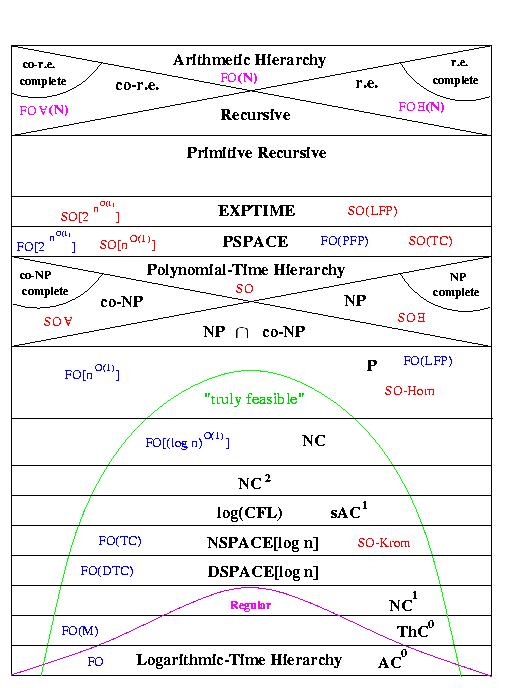
(this picture is from the cover of the book
"Descriptive Complexity" by
Neil Immerman)
|
For now, please see lecture notes from the previous run of this course and notes on computability and NP-completeness from an undergraduate course I taught before.
I will try to post updated notes if there are sufficient changes from before, new material, etc.
