COMP 6902, Spring 2018

11/7/2018 It was just pointed out to me that the " NP and NP-completeness" notes were missing the last three pages, which are exactly the pages on search-to-decision reduction needed for your assignment -- sorry for that! The notes have been fixed now, and the assignment deadline is extended till 11:55pm tomorrow (Thursday, July 12th).
9/7/2018 Presentations: so far, I have 5 groups doing presentations. Sudoku, Monochromatic Triangle and Colouring signed up to present on Wednesday, July 11 (this week), and Queens and Largest Common Subgraph are presenting on Monday, July 16th.
The presentations should be short (no more than 10 minutes total). You should describe your problem, reduction to SAT, say how you generated random instances, and give results of experiments you did (including the additional experiments you came up with).
If you are doing a presentation, please upload your slides to D2L. Also, let me know whether you would like to use my laptop or yours to show them.
If you want to do a presentation, but did not pick a date yet, please email me as soon as possible, indicating whether you would like to present this Wednesday or next Monday.
3/7/2018 Assignment 3 is now posted. Due Wednesday, July 11, 11:55pm. Type it up (in LaTeX) and upload pdf to D2L ; here is the LaTeX source,
3/7/2018 I will have office hours on Wednesdays July 4, 11, and 18, as well as Monday, July 16 (no office hours or lecture on July 9th).
2/7/2018 Here is the promised template for the project and an associated bibliography file . You are welcome to modify it as you see fit, but please try to include all the main components into your project report.
18/6/2018 A number of people have lost points on the reduction milestone because of forgetting to do some part of it. So please fix your reduction submission taking into account the feedback, and resubmit it by the evening of Thursday, June 21 (you only need to upload one file per group). Then I will update your mark to reflect your corrected submission.
17/6/2018 I will have office hours on Monday, June 18th from 1pm to 2pm.
14/6/2018 Remember that there are no lectures June 18 and June 20th ( semester break ). I am also away on June 25th. So the next lecture is June 27th.
After that, July 2nd is a holiday, and I will be away again on July 9th. As we had 2-hour-long lectures, we still should have covered all teaching hours two weeks before the official end of the semester. Thus, we can have our last class on July 18th; this is when we'll have the test. So the remaining classes are:
- Wed June 27th
- Wed July 4th
- Wed July 11th
- Mon July 16th
- Wed July 18th (test) .
13/6/2018 As discussed today in class, there is a change in the deadlines for the next several submissions, and an extra milestone for the project.
1. Assignment 2 is now due on Sunday, July 17, 11:55pm.
2. The next milestone for the project is now the description of the generator of your problem instances (to let me give you feedback on your generator before you write your code). The description of the generator is due at 11am on Wednesday, June 20th , and will be worth 15% of the project. Try to ensure that your generator can produce both "yes" and "no" instances of your problem reasonably frequently (you can use "planted" method as discussed in class if needed).
3. Both the reduction program and the generator program will be due on June 25th (10% of the project mark; this leaves 45% for the project report).
9/6/2018 For installing SAT solvers: if a solver has a file named "starexec_build", you might be able to install it with a command "bash starexec_build", at least on a Linux system.
8/6/2018 The deadline for the next project milestone, the reduction, is moved to June 11th (I will cover another reduction to SAT in Monday class).
6/6/2018 I will have extra office hours today (Wednesday) at 1pm. Please come if you would like to discuss your project.
3/6/2018 Assignment 2 is now posted. Due Friday, June 15, 7am. Type it up (in LaTeX) and upload pdf to D2L ; here is the LaTeX source,
3/6/2018 The set of notes on NP and NP-completeness just posted covers not only the last two lectures, but also the next several lectures. This is just for the reference: we may or may not cover the same material.
2/6/2018 Here is a detailed outline of the project , with some of the weight spread to intermediate milestones. The first milestone, due on Wednesday June 6, is to select a group and a problem, and upload your choice on D2L.
30/5/2018 The deadline for assignment 1 has been postponed for a day: it is now due Thursday, May 31, at 11:55pm. I will hold office hours tomorrow from 3pm to 4pm; please come if you have any questions (you are always welcome to email me if you have questions, as well).
23/5/2018 The updated source file now includes an example of a table for the TM transition function.
21/5/2018 To make 2c on the assignment simpler, print your resulting number on the output tape (but do move to the first symbol on that tape). Also, you can assume that tapes are two-way infinite, and that in addition to L and R, there is also a transition "S" (for "stay in place").
21/5/2018 Here is a tool for drawing finite automata which generates LaTeX code (copy just the part from \begin{center} to \end{center} into your file). Many thanks to Vineel for the link!
17/5/2018 Assignment 1 is now posted. Due Wednesday, May 30, 10pm. Type it up (in LaTeX) and upload pdf to Brightspace (former D2L); here is the LaTeX source,
7/5/2018 For the next little while, our lectures will be from 2pm to 4pm. This is to cover more material early on; we will skip lectures later in the semester.
14/5/2018 The next lecture, on May 16th, will be in the seminar room (EN-2022). Note that there is an exam there before us, so we might have to wait a little.
7/5/2018 On May 23rd, there is a useful workshop at MUN: Introduction to HPC with ACENET & Compute Canada / Introduction to Linux , followed by Introduction to Shell Scripting on May 24th. As the time on May 23rd overlaps with our class (2pm-4pm), we will cancel the class that day to allow everybody to attend these sessions. In particular, Introduction to Linux and Shell Scripting would be useful for you even if you don't use the clusters.
29/4/2018 The first lecture is Monday, May 7th. If you need me to sign your course add form, please bring it to class.

For typesetting please use LaTeX. I will post source files for the assignments. If you need a LaTeX compiler, the simplest way is to use an online one, such as ShareLaTeX. Just load the source file and start adding your solutions. A good, though outdated, introduction to LaTeX is "Essential LaTeX" .

Policy on collaboration: The work you submit must be your own. You may discuss problems from assignments with each other; however, you should prepare written solutions alone. Plagiarism is a serious academic offense and will be dealt with accordingly.

Course information

Description: The goal of this course is to help students develop an intuitive feel for hardness of computational problems, and an ability to prove that intuition. What does it mean that a given problem is "hard"? In which sense is it "hard": is it memory-intensive, computation-intensive; how are these notions related? How expressive are various languages used in databases and AI, and what does it mean computationally? These are some of the questions we will explore in this course.

In particular, we will cover the classical P vs. NP problem (is checking a solution easier than finding a solution? Nobody knows!), as well as classes of higher complexity (polynomial-time hierarchy), space classes, counting classes, randomized and circuit complexity, and descriptive and proof complexity. We will also review some computability theory and, time permitting, cover a range of advanced topics such as PCP, natural proofs (why it is hard to resolve the P vs. NP question), hardness of approximation, etc.

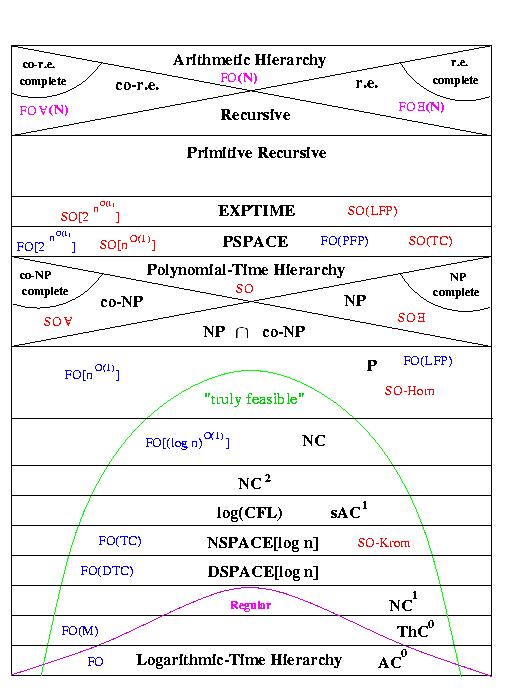
(this picture is from the cover of the book "Descriptive Complexity" by Neil Immerman)

COMP 6902 -- Theory of computation, Spring 2018

Announcements

Assignments and tests

Course information

Lecture Notes

Classic papers on computability and complexity: