Computer Science 6743 -- Complexity of Computational Problems, Winter 2010

Announcements

16/3/2010 Assignment 3 is now posted . Tentatively due March 23rd.
5/3/2010 The updated notes from Todd Wareham's guest lectures
3/3/2010 Here is a link to the notes from Todd Wareham's guest lectures
07/02/2010 Our midterm will be this Thursday, Feb 11th. After that, I will be away until March 7th. There will be no lectures on Feb 16th, 18th and 25th; on March 2nd and 4th Todd Wareham will substitute for me.
07/02/2010 Solutions to assignment 1 are now posted
02/02/2010 Assignment 2 is now posted.
29/01/2010 An example table from the notes is added to a1.tex. Feel free to modify it and add other features, if you like.
14/01/2010 I will be out of town until Jan 26th. Please email me if you have any questions!
06/01/2010 The first lecture is Thursday, Jan 7th.

Assignments and tests

For typesetting please use LaTeX. A good introduction to LaTeX is "Essential LaTeX" .

Course information

Lectures: 3:30-5pm Tuesdays and Thursdays in EN-1052 (officially). I will be travelling a lot this semester, so the actual schedule will be more erratic. Often we will have longer lectures followed by weeks of canceled classes.
Instructor: Antonina Kolokolova , email: [Your browser cannot view this email address] , office ER-6033.

Textbook: Computational Complexity: A Modern Approach by Sanjeev Arora and Boaz Barak.
The link is to the online version, containing an earlier draft of the book.
Reference book: M. Sipser: Introduction to the Theory of Computation (second edition).
We will also use lecture notes from similar courses (to be posted later).

Marking scheme (tentative!): 3 assignments 15% each, a midterm %15, a presentation 10%, and a final exam 30%.

Description: The goal of this course is to help students develop an intuitive feel for hardness of computational problems, and an ability to prove that intuition. What does it mean that a given problem is "hard"? In which sense is it "hard": is it memory-intensive, computation-intensive; how are these notions related? How expressive are various languages used in databases and AI, and what does it mean computationally? These are some of the questions we will explore in this course.

In particular, we will cover the classical P vs. NP problem (is checking a solution easier than finding a solution? Nobody knows!), as well as classes of higher complexity (polynomial-time hierarchy), space classes, counting classes, randomized and circuit complexity, and descriptive and proof complexity. We will also review some computability theory and, time permitting, cover a range of advanced topics such as PCP, natural proofs (why it is hard to resolve the P vs. NP question), hardness of approximation, etc.
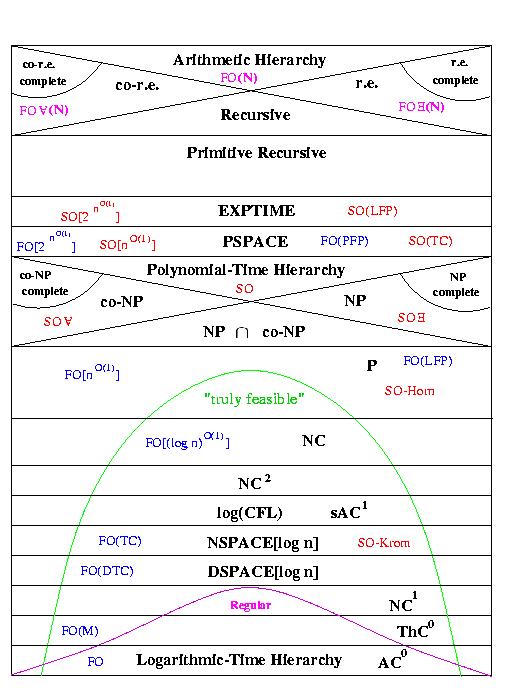
(this picture is from the cover of the book "Descriptive Complexity" by Neil Immerman)

Lecture Notes

For now, please see lecture notes from the previous run of this course and notes on computability and NP-completeness from an undergraduate course I taught before. I will try to post updated notes if there are sufficient changes from before, new material, etc.