| Announcements | | Course information | | Important dates | | Assignments and tests | | Lecture notes |
17/09/2008 I posted some links to (previous semester/course) course notes in the lecture notes section. I will try to post new versions of the notes whenever they are different, mistakes corrected, etc.
15/09/2008 The time slot for the course will be 2pm-3:30pm in the seminar room. The first lecture is Tuesday Sep 16th. We may be late starting the lecture since the seminar room is taken on that day until 2:30pm. I should still be there at 2pm, so please find me there.
16/07/2008 The time for the course is to be decided at the first
meeting. I will email everybody registered in the class to set up the
time for the first meeting. Better yet, email me if you are planning to register
with your preferred times and days.
For typesetting please use LaTeX. A good introduction to LaTeX is "Essential LaTeX" .
For now, please see lecture notes from the previous run of this course and notes on computability and NP-completeness from an undergraduate course I taught before. I will try to post updated notes if there are sufficient changes from before, new material, etc.
Course information
Lectures: TBA
Another book available online which you are welcome to use as a reference is
Computational Complexity: A Modern Approach by Sanjeev Arora and Boaz Barak. Description: The goal of this course is to help students develop an intuitive feel for hardness of computational problems, and an ability to prove that intuition. What does it mean that a given problem is "hard"? In which sense is it "hard": is it memory-intensive, computation-intensive; how are these notions related? How expressive are various languages used in databases and AI, and what does it mean computationally? These are some of the questions we will explore in this course. In particular, we will cover the classical P vs. NP problem (is checking a solution easier than finding a solution? Nobody knows!), as well as classes of higher complexity (polynomial-time hierarchy), space classes, counting classes, randomized and circuit complexity, and descriptive and proof complexity. We will also review some computability theory and, time permitting, cover a range of advanced topics such as PCP, natural proofs (why it is hard to resolve the P vs. NP question), hardness of approximation, etc. |
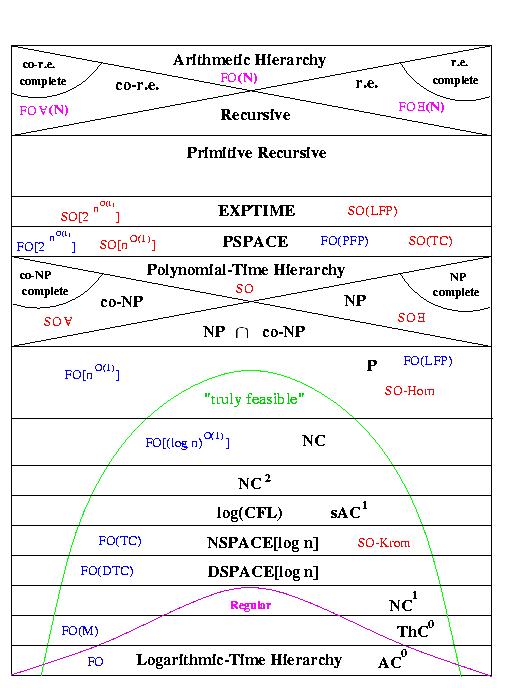 (this picture is from the cover of the book "Descriptive Complexity" by Neil Immerman) |