Continuous simulators [4] are characterized by the extensive use of mathematical formulae which describe how a simulated component responds when subjected to various conditions. For example, consider a circuit described at the transistor, resistor and capacitor level. The behaviour of all these components are well understood and are governed by several equations which describe their respective behaviours. A continuous simulator would apply those equations in the context of the components' environment and connectivity and produce a continuous graph which accurately reflects how the components would react if they were actually hooked up in reality. The graphs usually reflect the changes in the state of the system with respect to time; however, other relationships may also be demonstrated as well. Unfortunately, the mathematical equations employed by a continuous simulator can make the simulation very computationally intensive, especially in the presence of thousands of interconnected elements. As such, continuous simulators may be slow and are consequently only useful when simulating a relatively small number of components which are described at a low level of abstraction.
As an example of continuous simulation, consider a depletion
mode transistor acting as a pull up for a capacitive load [17].
The schematic for such a device is presented in Figure 1.1.
The transient behaviour of the system is governed by the equation
![]() .
.
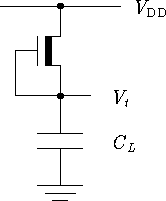
Figure 1.1: Depletion Mode Transistor Pulling Up Capacitive Load
During the latter stages of the rising transient, a continuous simulator would produce the graph given by Figure 1.2.
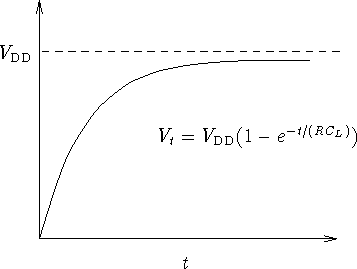
Figure 1.2: Graph Representing Continuous Behaviour