Due: Friday, 3 June at 10:00
- Linearize the nonlinear state-space model:
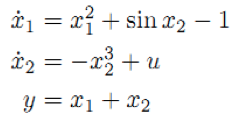
about the nominal value x1 = 1, x2 = 0, u = 0. That is, provide the A, B, C, and D matrices that can be used to describe the deviation about this nominal value. - Consider a two-dimensional system which has no input or output and is therefore represented only by A = [0 1; 0 0] (Matlab notation for a 2×2 matrix). Find the state transition matrix and find the state vector as a function of time for initial conditions [1; 1].
- Determine the transfer function for the following state-space system. Note, this is not to be done with Matlab (although it would be a good idea to use Matlab to check your answer). Remember that the transfer function is the frequency domain equivalent of the impulse response.
-

Note that ‘homogenous’ just means no input here. Also, feel free to use Matlab’s residue command for partial fraction expansion. - Continue the previous problem by assuming there is some input, consisting of a unit step of with magnitude 2. Determine the state vector at t = 4. The matrix B = [1; 0].
- Use Matlab to confirm the state vector computed at t = 4 for the previous two questions. The lsim command will be required.
