Due: Friday, 20 May at 10:00 (submit at the start of class)
2. For the following systems described by transfer functions, derive state-space realizations (define the state variables and the matrices A, B, C, and D). For problems (a) and (b) you should give in-depth workings. In both cases you should first determine the appropriate differential equation. For (b) you should define an intermediate signal w(t) and go through the steps as described in the notes.
For (c) and (d) you can use the pattern of coefficients to give the state-space realizations directly.
3. Determine the state-space realization for the circuit below. The input is voltage u(t). The output is the voltage across C2.
4. Determine the state-space realization for the mechanical system below. Note that the carts are assumed to have zero-friction contact with the ground. Let u(t) be the system’s input and p(t) the output.
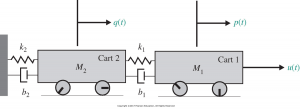
Hint: The viscous dampers are a potential source of confusion here. They represent physical connections between masses, such that one mass moving to the right will tend to drag any connected masses in the same direction. Normally it is the speed of a moving mass that governs the force of friction opposing that motion. This occurs here as well, but the relative speed of two connected masses generates the “dragging force” between them. In case this remains unclear, the following is the equation of motion for mass 1:
![]()
For spring k1 positive relative displacement supports the motion (i.e. has a positive sign). For viscous damper b1 the relative speed also supports the motion. Meanwhile, if mass 2 was stationary, this term would have a negative sign.
5. Use Matlab to determine the transfer functions corresponding to the following two systems:
(a)
(b)





