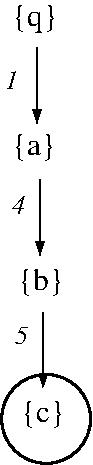Computer Science 3200, Fall '25
Course Diary

---

Copyright 2025 by H.T. Wareham and D. Churchill
All rights reserved

---

Week 1, Week 2, Week 3, Week 4, (In-class Exam #1 Notes),
Week 5, Week 6, Week 7, Week 8, Week 9, (In-class Exam #2 Notes),
Week 10, Week 11, (end of diary)

Tuesday, September 9 (Lecture #1)
[DC3200, Lecture #1; RN3, Chapter 1; Class Notes]

• Went over course outline.
  • Important note: Though this course was created by Dave Churchill, I am not teaching it the way Dave does. Differences include:
    • Different lecture topics / assignments / evaluation scheme.
    • Assignments done individually, not in teams.
    • Assignments in Python, not C++.
    • No lecture capture (though links will be given to Dave's recorded lectures on YouTube where appropriate).
    • No course Discord channel.

    For those who prefer Dave's 3200, he will be teaching it in the Winter 2026 semester.

• As this course is on algorithmic techniques for artificial intelligence, let us first give brief overviews of intelligence, artificial intelligence, and algorithms.
• What is intelligence?
  • Intelligence is at its heart the ability to perform particular tasks, e.g.,
    1. problem solving, e.g., playing complex games like chess and Go, proving mathematical theorems, logical inference.
    2. being creative, e.g., producing literature, music, or art, doing research.
    3. using tools to perform tasks
    4. social interaction with others
    5. remembering / learning
    6. talking
    7. seeing

  • Intelligence is typically associated with agents and the behavior these agents exhibit when interacting with an external environment (more on this in the next lecture).
  • Intelligence has often been seen as anything humans do that animals don't, e.g., proposed biological Kingdom-level class Psychozoa for humans (Huxley (1957)); as evidence has accumulated of lower-level intelligence in animals, e.g., gorilla communication by American Sign Language (ASL), counting by crows, memory in bees, complex social interaction and tool use by chimpanzees, intelligence has been redefined in terms of complex high-level tasks, e.g., (1-2) above, to preserve human superiority.
  • This view of intelligence as exclusively human (and high-level adult human at that) surfaces in what we find anomalous (and funny), e.g., "Children / animals can't do that!"
  • Example: Not the Nine O'Clock News (1980): Gerald the Gorilla (Link)
• What is artificial intelligence (AI)?
  • Mythology and history are filled with artificial creatures that exhibited the appearance of (if not actual) intelligence, e.g., the bronze giant Talos, Roger Bacon's talking bronze head, European clock and musical automata, Vaucanson's mechanical duck (1739).
  • The term "artificial intelligence" was coined by John McCarthy to describe the goal of a two-month summer workshop held at Dartmouth College in 1956. AI is essentially the implementation of intelligent abilities by machines (in particular, electronic computers).
  • Many AI application areas, e.g.,
    • Problem solvers, e.g., General Problem Solver (GPS), artificial theorem provers, chess and Go programs (Deep Blue (1997); AlphaGo (2016)).
    • Logical / probabilistic reasoning systems, e.g., expert systems, Bayesian networks.
    • Generative AI, e.g., ChatGPT, DALI
    • (Swarm) Robotics
    • Machine learning
    • Natural Language Processing (NLP)
    • Computer Vision

  • Can distinguish types of AI based on mode of implementation (weak / strong), implementation mechanisms (symbolic / connectionist), and extent of implemented ability (Artificial Specialized Intelligence (ASI) / Artificial General Intelligence (AGI)).
    • Strong AI uses computational approximation of human / natural cognitive mechanisms; Weak AI uses any possible computational mechanisms.
    • Symbolic AI uses computer programs operating within discrete-entity frameworks, e.g., logic; Connectionist AI uses approximations of biological brain mechanisms, e.g., neural networks.
    • ASI implements a single intelligent ability, e.g., recognizing faces, answering questions, playing chess; AGI implements all intelligent abilities performed by a human being.
  • The initial focus of AI research was on strong symbolic ASI for high-level intelligent abilities (tasks (1-2) above) with the hope that developed ASI modules could be combined to create AGI. However, given the difficulties of implementing even supposedly low-level intelligent abilities (tasks (3-7) above), let alone AGI, current research tends more to weak connectionist ASI.
  • Though it has gone through several "winters" in the last 65+ years (Haigh (2023a, 2023b, 2024a, 2024b, 2025)), AI is currently in a boom period, with weak connectionist systems exhibiting seemingly human- (and sometimes trans-human-) level performance, e.g., ChatGPT, medical image analysis.
  • It is important to keep the distinctions made above in mind, particularly between ASI and AGI; it is often in the interests of researchers and corporations to claim that their systems do far more they than they actually do, and the resulting expectations can have embarrassing, e.g., automated machine (mis)translation, or even lethal, e.g., (non-)autonomous vehicles, consequences.
• What is an algorithm?
  • Classical CS definition: Given a problem P which specifies input-output pairings, an algorithm for P is a finite sequence of instructions which, given an input I, specifies how to compute that input's associated output in a finite amount of time.
  • This is the type of algorithm underlying symbolic GOFAI (Good Old-Fashioned AI); such algorithms are both created (hand-crafted) and understandable by humans.
  • Many modern AI systems have broadened the term "algorithm" to methods derived by machine learning systems that have been trained on massive amounts of data; such algorithms are machine-crafted and in many cases not easily understandable by humans, e.g., BERTology = the field of research devoted to trying to understand why the NLP BERT Large Language Model produces the outputs that it does.
  • It is critically important to keep the hand-crafted / machine-crafted distinction in mind given emerging challenges in real-world AI.
    • In order for AI systems to operate in tandem with humans or autonomously, these systems must be trustworthy (Schneier (2025)), i.e.,
      • These systems are reliable, i.e., they produce wanted behaviors consistently;
      • These systems are fair, i.e., they do not encode bias that compromises their behavior; and
      • These systems are explainable, i.e., the reasons why a system makes the decisions it does can be recovered in an efficient manner.

      While these properties can be ensured in hand-crafted, algorithms, it is not yet known if this can be done (even in principle, let alone efficiently (Buyl and De Bie (2024); Adolfi et al (2024a, 2024b, 2025)) for machine-crafted algorithms.

• AI is most certainly in an exciting yet unnerving state at present (Denning (2025)), but if one can forego knee-jerk panic, there are many opportunities for both applying existing and developing new algorithmic techniques for AI.
• In this course, we will first look at symbolic hand-crafted algorithmic techniques (search (single agent / multi-agent), constraint satisfaction, logical reasoning, planning) and then move on to symbolic and connectionist machine-crafted techniques (evolutionary computation, reinforcement learning, neural networks and deep learning).
• But before all that, next lecture, a closer look at agents and environments -- see you then!
• Potential exam questions

Thursday, September 11 (Lecture #2)
[DC3200, Lecture #2; RN3, Chapter 2; Class Notes]

• Agents and Environments
  • Agents
    • An agent exists and performs intelligent behaviors, e.g., makes decisions and takes actions, in a specific environment and interacts with that environment via a sense-understand-plan-act loop, i.e.,

      

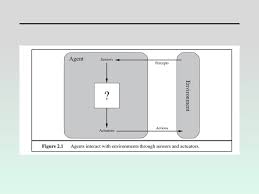
    • An agent perceives its environment through sensors, e.g., camera, touch, taste, keyboard input; these sensors provide percepts, which form percept sequences over time.
    • Agents act in their environment through actuators, e.g., limbs, tools, allowable moves in a game; actuators perform actions that can modify the environment (including the agent's internal state and/or position in the environment).
    • An agent's choice of action is specified as an agent function and implemented as an agent program relative to a particular architecture.
      • Agent functions are also known as policies and there are various names for agent programs depending on the application, e.g., controllers (robotics).
      • In general, an agent's action-choice can depend on its entire percept-history to date; however, we will in this course focus an agents whose action-choices depend on the current percept.
      • There are typically many ways to implement an agent function, e.g., lookup tables, IF-THEN statement blocks, neural networks.
    • An agent may have knowledge about its environment, e,g., environment model, game rules / allowable moves.
    • EXAMPLE: Some example agents:
      • A change machine
      • A vending machine
      • Roomba vacuum cleaner
      • Human players in a game of chess
      • Self-driving vehicle
      • AI personal assistant
      What are the sensors, percepts, actuators, actions, and knowledge (if any) associated with each of these agents?
    • An agent may have multiple internal states, with percept / action pairs between these states encoded in a state-transition function.
    • EXAMPLE: Three deterministic finite-state agents that operate in a 2D grid-world (Wareham and Vardy (2018)).

      

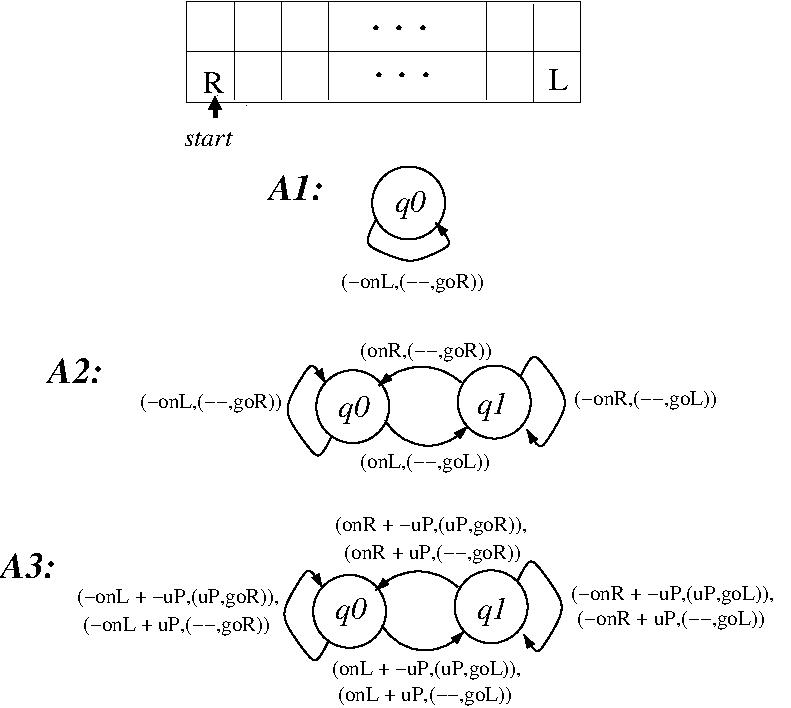
      • State transitions are specified as (state, percept, action, state) tuples, where an action is specified as an (environment-change, agent move) pair.
      • Agent processing starts in state q0.
      • What does each of these agents do?
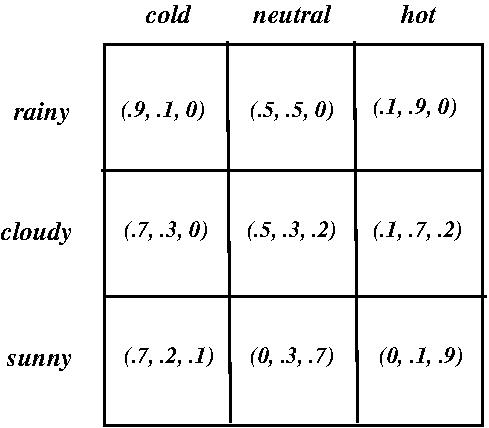
    • EXAMPLE: A stochastic agent
      • Specified as a table whose x- and y-axes are percepts and table entries are probability-vectors specifying the probabilities of a set of actions relative to a set of x/y-percept combinations.
      • Consider the following agent which specifies the probabilities of what to do (wear coat, carry umbrella, do nothing extra) if you want to take a walk outside depending on the weather ((rainy / cloudy / sunny) x (cold / neutral / hot)):

        

    • A rational agent does the best possible action at each point wrt optimizing some pre-defined performance measure; such an agent has an optimal policy.
      • Note that rationality is NOT omniscience, i.e., knowing the complete environment and the outcomes of all (even random) actions.
      • EXAMPLE: Going across street at crosswalk to see friend vs not crossing street because of incoming meteor from space.
    • Four basic types of agents:
      1. Simple reflex agents

         

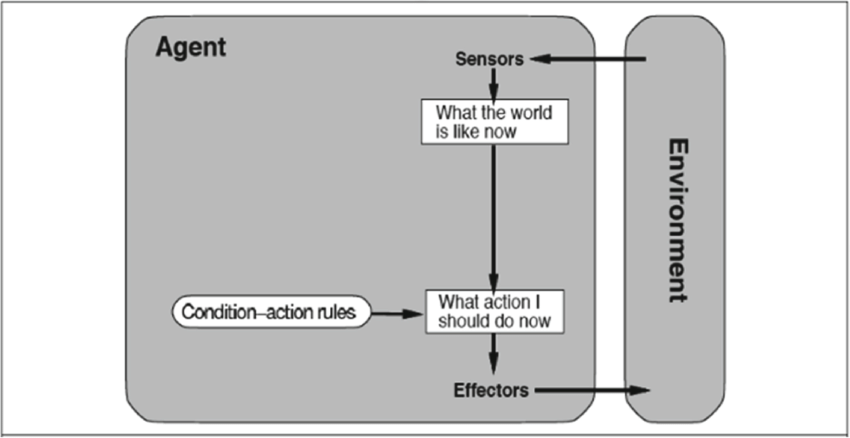
         • This simplest type of agent reacts without understanding or planning by using sets of encoded IF-THEN rules that directly link percepts and actions, e.g., the stochastic and one-state deterministic finite-state agents given above, a change machine.
         • The intelligence encoded in such agents can be impressive, e.g., Brooks' Genghis robot, basic obstacle avoidance in self-driving vehicles, but are ultimately limited in that there is little understanding or planning in the action-selection process.
      2. Model-based agents

         

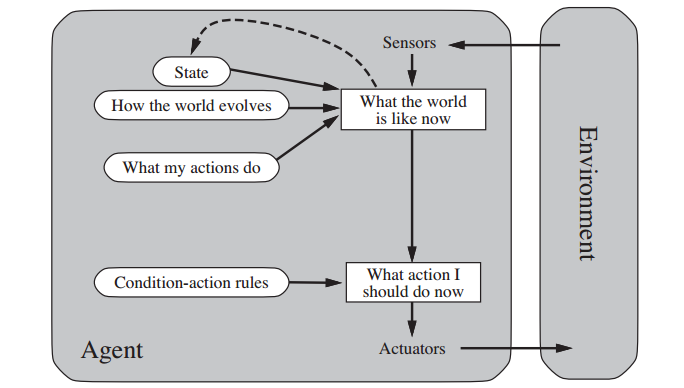
         • This type of agent maintains a non-trivial internal state that incorporates knowledge of how the world works and a model of the world encountered to date (including the agent's own past actions in the world, e.g., both of the two-state deterministic finite-state agent given above, a vending machine).
         • The intelligence encoded in such agents now allows understanding to be part of the action-selection process.
      3. Goal-based agents

         

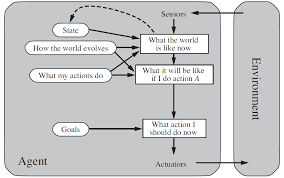
         • This type of agent incorporates a description of an agent's wanted goal, e.g., the destination to be reached, as well as a way of evaluating if that goal has been achieved, e.g., are we at the requested destination?
         • Typically more complex than simple reflex agents but much more flexible in terms of the intelligence it can encode (in particular, planning as part of the action-selection process).
      4. Utility-based agents

         

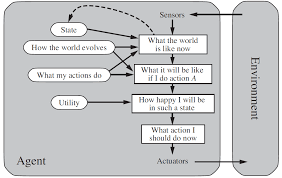
         • This type of agent incorporates a utility function that internalizes some performance measure, e.g., the distance traveled on a particular path from the start point to the destination, and is thus capable of optimizing this performance measure, e.g., choosing the shortest path from a start point to the destination.
         • Such agents are more complex still but can (given an appropriate utility function) encode general rationality.
         • Note that choosing the appropriate utility function is crucial to the encoded degree of rationality and this is typically very hard to do.
    • The intelligence in the four types of agents above is hard-coded using hand-crafted algorithms. The most complex type of agent can learn from experience and both become rational and maintain this rationality in the face of changing environments. The resulting agent programs are machine-crafted and will be discussed in the final lectures of this course.

Tuesday, September 16 (Lecture #3)
[ DC3200, Lecture #2 and DC3200, Lecture #3; RN3, Chapters 2 and 3; Class Notes]

• Agents and Environments (Cont'd)
  • Environments
    • The current configuration of an environment is that environment's current state.
      • A configuration encodes all entities in an environment, including the agents (and, if applicable, the positions and internal states of these agents) within the environment.
      • EXAMPLE: A configuration of a Solitaire card game would show all cards and their order, both in the visible stacks of cards and the deck of undrawn cards.
      • What an agent perceives may not be a complete representation of an environment's state; however, such observations are all the agent has to make its decisions.
      • EXAMPLE: An agent playing a game of Solitaire can only see the visible stacks of cards and their orders in these stacks.
    • Environments can be viewed as problems to which agents provide solutions, e.g., a path between locations on a map, a sequence of rule-applications that results in a wanted goal.
    • EXAMPLE: Some example agents:
      • Roomba vacuum cleaner
      • Human players in a game of chess
      • Self-driving vehicle
      • AI personal assistant
      What are the environments, environment configurations, and problems associated with each of these agents?
    • Environments have associated state and action spaces.
      • State space = the number of possible configurations of the environment.
      • Action space = the number of possible actions relative to a state.
      • Average / worst-case measures of the sizes of state and action spaces are frequently used as measures of environment complexity.
        • Are good measures of the computational complexity of searching state / action spaces by exhaustive search.
      • EXAMPLE: State space sizes for some games
        • Tic-Tac-Toe: 10^4
        • Chess: 10^{43}
        • Go: 10^{172}
      • EXAMPLE: Total # sequences of actions in some game (game tree complexity)
        • Tic-Tac-Toe: <= 10^5
        • Chess: <= 10^{123}
        • Go: <= 10^{360}
        • Starcraft II: > 10^{1000)
      • Given that there are approximately 10^{80} atoms in the universe and these atoms are expected to decay into a quark mist in 10^{70} years, the opportunities for completing exhaustive searches for the largest state spaces are severely limited; that is why you need the smartest search algorithms possible (some of which we will be looking at over the next several lectures).
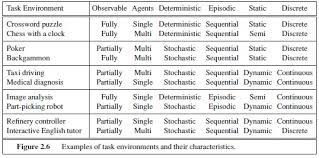
    • Environments have several properties:
      • Fully vs partially observable by agent, e.g., chess vs poker.
      • Deterministic vs stochastic from viewpoint of agent, e.g., chess vs poker.
      • Episodic vs sequential, i.e., next episode does not or does depend on previous episodes, e.g., OCR (Optical Character Recognition) vs chess.
      • Static vs dynamic, i.e., environment changes discretely when agents act or continuously (possibly even during agent decision), e.g., turn-based (chess) vs real-time (Starcraft) games.
      • Discrete vs continuous conception of time and environment change, e.g., poker /chess vs self-driving vehicles.
      • Single agent vs multiple agents, e.g., Solitaire vs chess vs self-driving vehicles.
      • Complete vs incomplete knowledge of actions and their consequences, e.g., chess vs real life.
    • Example environments and their properties:

      

    • EXAMPLE: Some example agents:
      • Roomba vacuum cleaner
      • Human players in a game of chess
      • Self-driving vehicle
      • AI personal assistant
      What are the properties of the environments associated with each of these agents?
    • The properties of an environment dramatically affect the computational difficulties of designing agents for and operating agents within that environment (e.g., what is the envonment in which a boat operates and what can the boat observe?); we will see this in action over the course of our lectures, many of which will consider only the simplest environments..
• Potential exam questions
• Problem-solving and search
  • Problem-solving agents are rational agents that act in environments to solve the problems posed by those environments.
    • In the simplest case, they are goal-based agents that find a sequence of actions that satisfies some goal, e.g., find a path from a start point to a given destination.
    • More complex cases involve utility-based agents that find a goal-achieving sequence of actions that optimize some performance measure, e.g., find a shortest path (in terms of distance traveled) from a start point to a specified destination.
    • EXAMPLE: Finding a (shortest) path from our classroom at MUN to the Winners store at the Avalon Mall.
    • A solution (also known as a solution path) is a sequence of actions that terminates in the problem's goal.
  • A well-defined problem consists of:
    1. An initial state that the agent starts in.
    2. The actions possible from each state.
       • Specified as a successor function, e.g., from position (x,y) in a 2D grid-based maze, you can go up, down, left, or right.
       • This is typically refined relative to each state to the viable actions for that state, i.e., the actions that do not violate constraints like moving into a wall in a 2D maze.
    3. The set of goal states
       • Specified as a goal test function that returns "Yes" if a given state is in the set of goal states and "No" otherwise, i.e., are we just outside the main door of the Winners store at the Avalon Mall? Is our chess opponent in checkmate?
    4. Action cost function
       • Most problems assume positive non-zero action costs.
  • The cost of a solution is the sum of the costs of the actions in that solution's associated path; an optimal solution has the lowest cost over all possible solutions.
  • EXAMPLE: Shortest path between two vertices in an edge-weighted graph G.
    • Problem definition:
      1. Start vertex in G.
      2. For each vertex v in G, the set of edges with v as an endpoint.
      3. Destination vertex in G.
      4. Edge-weight function for G.
    • The problem objective is to find a shortest (in terms of summed edge-weights) path in G from the start vertex to the destination vertex.
  • EXAMPLE: Shortest path between two locations in a 2D grid G incorporating obstacles.
    • Problem definition:
      1. Start location in G.
      2. For each location l in G that is not part of an obstacle, the subset of possible moves {up, down, left, right} that do not land on some obstacle when executed at l.
      3. Destination location in G.
      4. Function that assigns cost 1 to up, down, left, and right moves.
    • The problem objective is to find a shortest (in terms of # of moves) path in G from the start location to the destination location.

Thursday, September 18 (Lecture #4)
[DC3200, Lecture #3; RN3, Chapter 3; Class Notes]

• Problem-solving and search (Cont'd)
  • EXAMPLE: Most efficient plan for making a cup of tea.
    • Problem definition:
      1. State consisting of {cup(empty), teaBag, kettle(empty), faucet, electricity}.
      2. The set A of actions, i.e.,
         1. kettle(empty) + faucet => -kettle(empty) + kettle(fullCold)
            [fill kettle with cold water]
         2. cup(empty) + faucet => -cup(empty) + cup(fullCold)
            [fill cup with cold water]
         3. kettle(fullCold) + electricity => -kettle(fullCold) + kettle(fullHot)
            [boil kettle]
         4. cup(fullCold) + electricity => -cup(fullCold) + cup(fullHot)
            [boil cup]
         5. cup(empty) + teaBag => -teaBag + -cup(empty) + cup(teaBag)
            [add tea bag to cup]
         6. cup(empty) + kettle(fullHot) => -cup(empty) + cup(fullHot)
            [add hot water to cup]
         7. cup(teaBag) + kettle(fullHot) => -cup(teaBag) + cup(tea)
            [make tea I]
         8. cup(fullHot) + teaBag => -cup(fullHot) + -teaBag + cup(tea)
            [make tea II]

         Each action X => Y (where X is the cause and Y is the consequence) is an IF-THEN rule whose application to a state s is viable if for each x (-x) in X, x is (not) in s and results in a state s' that modifies s by adding (removing) each y to (from) s such that y (-y) is in Y, e.g., the initial state is modified to state s' = {cup(teaBag), kettle(empty), faucet, electricity} by the application of action 5.
         Given the above, for each possible state s that is a subset of {faucet, electricity, kettle(empty), kettle(fullCold), kettle(fullHot), teaBag, cup(empty), cup(fullCold), cup(fullHot), cup(teaBag), cup(tea)}, the set of viable actions for s is the subset of A that can be viably applied to s.

      3. Any state including {cup(tea)}.
      4. Function that assigns cost 1 to each action.
    • The problem objective is to find a most efficient (in terms of # of actions) plan that, starting in the initial state, creates a hot cup of tea.
    • The formalism above is a simplified version of the input language for the STRIPS (STanford Research Institute Problem Solver) automated planning system (Fikes and Nilsson (1971); see also Bylander (1994)) and will be used in Assignment #1.
    • The type of state in this problem has what is known as a factored representation, i.e., a state with a multi-component internal structure; we will be using this type of problem-state frequently later in the course.
  • Search is the process of exploring a problem's search space to find a solution. This process generates a search tree in which the root node, edges, and non-root nodes correspond to the initial problem state, actions, and possible solution paths.
    • Starting with the root node, the search tree is generated by expanding nodes, i.e., generating the nodes reachable from a node n by viable actions, in some specified manner until either a goal node is found or it is established that no goal-state is reachable by any sequence of actions starting at the root node.
      • At each point in this process, the list of leaf nodes that has been generated but not yet expanded is known as the fringe.
      • Search algorithms can be distinguished in how they select nodes from the fringe to expand.
    • Each search tree node corresponds to problem state; however, if actions are reversible, a problem state can be associated with multiple search tree nodes and a finite-size problem state space can have an infinite-size search tree.
    • EXAMPLE: Search tree for problem of finding a shortest path between two vertices in a graph. [DC3200, Lecture #3, Slides 14-26 (PDF)]
    • EXAMPLE: Search tree for 15 puzzle [DC3200, Lecture #3, Slides 27-28 (PDF)]
    • Must distinguish problem-states and search-tree nodes - the former are configurations of the problem environment and the latter are bookkeeping data structures allowing recovery of solution paths to goals. To this send, a search tree node n typically contains the following data:
      • The problem state associated with n.
      • A pointer to n's parent node, i.e., the node whose expansion generated n.
      • The action by which n was generated from its parent node.
      • The cost of the sequence of actions on the path in the search tree from the root node to n.
        • This is traditionally denoted by g(n).
      • The depth of n, i.e., the number of actions on the path in the search tree from the root node to n.
      Additional data may also be stored in the node depending on the search algorithm used.
    • ALGORITHM: General uninformed tree search

      1.   Function Tree-Search(problem, strategy)
      2.     fringe = {Node(problem.initial_state)}
      3.     while (true)
      4.       if (fringe.empty) return fail
      5.       node = strategy.select_node(fringe)
      6.       if (node.state is goal) return solution
      7.       else fringe.add(Expand(node, problem))
      

    • ALGORITHM: Node expansion [ASSIGNMENT #1]

      1.   Function Expand(node, problem)
      2.     successors = {}
      3.     for a in viablActions(problem.actions, node)
      4.       s = Node(node.state.do_action(a))
      5.       s.parent = node
      6.       s.action = a
      7.       s.g = node.g + s.action.cost
      8.       s.depth = node.depth + 1
      9.       successors.add(s)
      10.    return succesors
      

    • We will build on these algorithms below when we consider different search strategies.
  • Search strategies
    • Measures for assessing the problem-solving performance of a search-strategy algorithm s:
      1. Completeness, i.e., is s guaranteed to find a solution if it exists?
      2. Optimality, i.e., is s guaranteed to find an optimal solution?
      3. Time complexity, i.e., how long does it take for s to find a solution or establish that a solution does not exist?
         • Measures the total number of search tree nodes generated.
      4. Space complexity, i.e., how much memory is needed to execute s?
         • Measures the maximum number of search tree nodes that must be stored at any point in the search process.

      Aspects of the search tree typically used to derive time and space complexity functions are the branching factor b (the maximum number of successor nodes for any tree node) and the depth d (of the shallowest goal node, if a solution exists, and the maximum depth of a generated node, if one does not). Note that the size of a search tree is upper-bounded by b^{d+1}.

    • Two categories of search strategies:
      • Uninformed (blind) search
        • Has no extra information about states in a search tree beyond that in the problem description, i.e., algorithm operations limited to successor, generation, and goal test.
      • Informed search
        • Has extra information which allows guesses about which states are more likely to be on useful / optimal solution paths, i.e., algorithm operations additionally include the value of heuristic node evaluation function h(n).
        • Hopefully leads to faster search.
      We will look first at uninformed search strategies and then move on to informed search strategies, with an intermediate stop to consider closed lists, a key algorithmic technique for optimizing the performance of both types of search strategies.
  • Uninformed (blind) search strategies
    • Breadth-First Search (BFS)
      • Root node is expanded first, followed its successors, followed by their successors, and so on.
      • As such, all nodes at a given depth are expanded before any nodes in the next level; this is done by implementing the fringe-set as a queue.
      • ALGORITHM: BFS [ASSIGNMENT #1]

        1.   Function BFS(problem)
        2.     fringe = Queue{Node(problem.initial_state)}    <=
        3.     while (true)
        4.       if (fringe.empty) return fail
        5.       node = fringe.pop()                          <=
        6.       if (node.state is goal) return solution
        7.       else fringe.add(Expand(node, problem))
        

        Lines modified from the algorithm for general uninformed tree search are indicated by "<=".
      • EXAMPLE: BFS for a shortest (# edges) path between vertices A and C in an unweighted graph. [DC3200, Lecture #3, Slides 44-48 (PDF)]
      • EXAMPLE: BFS for a shortest (Manhattan distance) path between two locations in a 2D grid with obstacles [DC3200, Lecture #3, Slides 49-54 (PDF)]
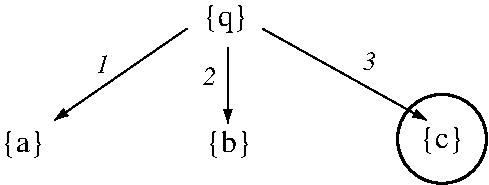
      • EXAMPLE: BFS for a shortest (summed action-cost) solution to a modified STRIPS planning problem based on facts [q, a, b, c], initial state [q], goal state [c], and actions
        1. q => -q + a (cost 1)
        2. q => -q + b (cost 1)
        3. q => -q + c (cost 1)
        4. a => -a + b (cost 1)
        5. b => -b + c (cost 1)
        

      • Performance of BFS
        • BFS is complete.
          • BFS can explore the entire search tree; hence, if there is a goal node in the tree, BFS will find it.
          • Note that if there are multiple goal nodes in the search tree, BFS will find the shalowest one.
        • BFS is not optimal in general.
          • This is because the path to the shallowest goal node need not have the optimal cost.
          • EXAMPLE: BFS is not optimal for finding a shortest (summed edge-weights) path between vertices A and C in an edge-weighted graph. [DC3200, Lecture #3, Slide 57 (PDF)]
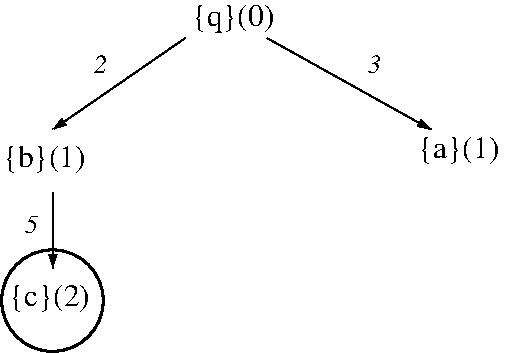
          • EXAMPLE: BFS is not optimal in finding a shortest (summed action-cost) solution to a modified STRIPS planning problem based on facts [q, a, b, c], initial state [q], goal state [c], and actions
            1. q => -q + c (cost 5)
            2. q => -q + b (cost 1)
            3. q => -q + a (cost 1)
            4. a => -a + b (cost 2)
            5. b => -b + c (cost 1)

            

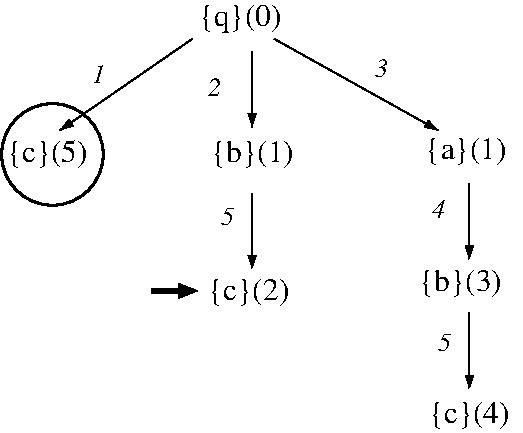
          • BFS is optimal if (1) path costs never decrease as depth increases or (2) all action costs are the same.
        • Time Complexity: O(b^{d+1}), as all nodes in a search tree of depth d with branching factor b may be generated.
        • Space Complexity: O(b^{d+1}), as all generated nodes must be stored in memory to allow reconstruction of solution paths from goal nodes via parent pointers.

Tuesday, September 23 (Lecture #5)
[DC3200, Lecture #3; RN3, Chapter 3; Class Notes]

• Problem-solving and Search (Cont'd)
  • Uninformed (blind) search strategies (Cont'd)
    • Uniform Cost Search (UCS)
      • At each point, the node with the smallest path cost, i.e., g(n)-value, is expanded; this is done by implementing the fringe-set as a priority queue wrt g(n).
        • UCS is essentially Dijkstra's algorithm!
      • UCS works only if all action cost are > 0; otherwise, can enter an infinite loop.
      • ALGORITHM: UCS [ASSIGNMENT #1]

        1.   Function UCS(problem)
        2.     fringe = PriorityQueue{Node(problem.initial_state)}    <=
        3.     while (true)
        4.       if (fringe.empty) return fail
        5.       node = fringe.min_g_value()                          <=
        6.       if (node.state is goal) return solution
        7.       else fringe.add(Expand(node, problem))
        

        Lines modified from the algorithm for general uninformed tree search are indicated by "<=".
      • EXAMPLE: UCS for a shortest (summededge-weights) path between vertices A and C in an edge-weighted graph. [DC3200, Lecture #3, Slide 57 (PDF)]
      • EXAMPLE: UCS for a shortest (summed action-cost) solution to a modified STRIPS planning problem based on facts [q, a, b, c], initial state [q], goal state [c], and actions
        1. q => -q + c (cost 5)
        2. q => -q + b (cost 1)
        3. q => -q + a (cost 1)
        4. a => -a + b (cost 2)
        5. b => -b + c (cost 1)
        

      • Performance of UCS
        • UCS is complete
        • UCS is optimal if action costs > 0 (epsilon)
        • Time Complexity: O(b^{1 + floor(C*/epsilon)}), where C* is the cost of an optimal solution
          • This is necessary because path cost is no longer linked to depth.
          • Can be much bigger than b^{d+1} is the worst case.
        • Space Complexity: O(b^{1 + floor(C*/epsilon)})
    • Depth-First Search (DFS)
      • At each point, the node with the greatest depth is expanded; if a non-goal node is reached with no successors, DFS backs up and resumes search at the previous depth.
      • This can be done by implementing the fringe-set as a stack, but is more commonly done using recursion
      • ALGORITHM: DFS (non-recursive) [ASSIGNMENT #1]

        1.   Function DFS(problem)
        2.     fringe = Stack{Node(problem.initial_state)}    <=
        3.     while (true)
        4.       if (fringe.empty) return fail
        5.       node = fringe.pop()                          <=
        6.       if (node.state is goal) return solution
        7.       else fringe.add(Expand(node, problem))
        

        Lines modified from the algorithm for general uninformed tree search are indicated by "<=".
      • ALGORITHM: DFS (recursive)

        1.   Function DFS(node, problem)
        2.     if (node.state is goal) return solution
        3.     successors = Expand(node, problem)
        4.     for (s in successors):
        5.       result = DFS(s, problem)
        6.       if (result != "no solution")
        7.         resturn result
        8.     return "no solution"
        
             Call DFS(root_node, problm)
        

      • EXAMPLE: DFS for a solution to a modified STRIPS planning problem based on facts [q, a, b, c], initial state [q], goal state [c], and actions
        1. q => -q + c (cost 1)
        2. q => -q + b (cost 1)
        3. q => -q + a (cost 1)
        4. a => -a + b (cost 1)
        5. b => -b + c (cost 1)
        

      • Performance of DFS
        • DFS is not complete in general
          • Can enter infinite loop if does not keep track of already-visited states.
          • EXAMPLE: DFS for a path between vertices A and B in an unweighted graph. [DC3200, Lecture #3, Slide 57 (PDF)]
          • Infinite loops can be prevented by algorithm enhancements (see DLS and ID-DFS below) or by the use of closed lists (see below).
        • DFS is not optimal in general
          • This is because it returns the first goal found.
          • EXAMPLE: If B is visited before D, DFS is not optimal for finding a shortest (summed edge-weight) path between vertices A and C in an edge-weighted graph. [DC3200, Lecture #3, Slide 57 (PDF)]
          • EXAMPLE: DFS is not optimal for finding a shortest (either # moves or summed action-cost) solution to the modified STRIPS planning problem given above.
        • Time Complexity: O(b^m), where m is is the depth of the deepest node.
        • Space Complexity: O(bm)
          • This is because in the worst case, DFS stores a path of m nodes from the route along with the b successors of each node on this path.
    • Depth-Limited Search (DLS)
      • Solves the infinite-loop DFS problem by limiting the maximum search depth to some L > 0.
      • ALGORITHM: DLS (recursive)

        1.   Function DLS(node, L, problem)
        2.     if (node,depth > L) return "no solution"       <=
        3.     if (node.state is goal) return solution
        4.     successors = Expand(node, problem)
        5.     for (s in successors):
        6.       result = DLS(s, L, problem)
        7.       if (result != "no solution)
        8.         return result
        9.     return "no solution"
        
             Call DLS(root_node, L, problm)
        

        Lines modified from the algorithm for DFS (recursive) are indicated by "<=".
      • Performance of DLS
        • DLS is not complete when solution depth > L
        • DLS is not optimal in general
          • This is because it returns the first goal found.
        • Time Complexity: O(b^L)
        • Space Complexity: O(bL)
    • Iterative Deepening Depth-First Search (ID-DFS)
      • In DLS, one chooses maximum search depth L by analysis of the problem's state space; alternatively, one can gradually increase the depth limit until a solution is found. This is what ID-DFS does.
      • ALGORITHM: ID-DFS

        1.   Function ID-DFS(node, , problem)
        2.     for d in (1,infty)
        3.       result = DLS(node, d, problem)
        4.       if (result != "no solution") return result
        5.     return "no solution"
        

      • Performance of ID-DFS
        • ID-DFS is complete
        • ID-DFS is optimal under same conditions as BFS
        • Time Complexity: O(b^{d+1}), where d is the depth of the shallowest goal node
          • As nodes may be recomputed as L is increased, may seem wasteful; however, in practice, generates about twice as many nodes as BFS.
        • Space Complexity: O(bd)
        As it combines the advantages of both BFS and DFS, ID-DFS is in general preferable to both BFS and DFS.
    • TABLE: Uninformed search strategy comparison [DC3200, Lecture #3, Slide 79 (PDF)]
    • INTERLUDE: A look at the mechanics of Assignment #1.
      • How do you modify the BFS, UCS, and DFS (non-recursive) algorithms above to print all solutions to a given problem?
    • None of the algorithms presented above remember the states that have already been expanded. Such states lead to duplicated effort and (if actions are reversible) infinite loops. Such states can be remembered and avoided using closed lists, which are lists of previously expanded (and hence explored) nodes.
      • To ensure efficient lookup, closed lists are often implemented using dictionaries and hash tables.
    • In addition to eliminating infinite loops, such lists can lead to an exponential savings in the number of nodes generated; however, these lists are not universal cures for all of the ills that can plague search (see below).
    • Following terminology in Russell and Norving, tree search algorithms that use closed lists (1) rename fringe lists as open lists and, perhaps more confusingly, (2) are renamed graph search algorithms (after the classic BFS graph search algorithm that implements closed lists implicitly using a node coloring scheme to avoid re-exploring previously-encountered vertices).
    • ALGORITHM: General uninformed graph-based search

      1.   Function Graph-Search(problem, strategy)
      2.     closed = {}                                 <=
      3.     open = {Node(problem.initial_state)}
      4.     while (true)
      5.       if (fringe.empty) return fail
      6.       node = strategy.select_node(open)
      7.       if (node.state is goal) return solution     
      8.       if (node.state in closed) continue        <=
      9.       closed.add(node.state)                    <=
      10.      open.add(Expand(node, problem))
      

      Lines modified from the algorithm for general uninformed tree search are indicated by "<=".
    • ALGORITHM: Graph-based BFS

      1.   Function gbBFS(problem)
      2.     closed = {}                                 <=
      3.     open = Queue{Node(problem.initial_state)}     
      4.     while (true)
      5.       if (fringe.empty) return fail
      6.       node = open.pop()                           
      7.       if (node.state is goal) return solution   
      8.       if (node.state in closed) continue        <=
      9.       closed.add(node.state)                    <=
      10.      open.add(Expand(node, problem))
      

      Lines modified from the algorithm for (tree-based) BFS are indicated by "<=".
    • ALGORITHM: Graph-based DFS

      1.   Function gbDFS(problem)
      2.     closed = {}                                 <=
      3.     open = Stack{Node(problem.initial_state)}     
      4.     while (true)
      5.       if (fringe.empty) return fail
      6.       node = open.pop()                           
      7.       if (node.state is goal) return solution   
      8.       if (node.state in closed) continue        <=
      9.       closed.add(node.state)                    <=
      10.      open.add(Expand(node, problem))
      

      Lines modified from the algorithm for (tree-based) DFS are indicated by "<=".
    • Graph-based search algorithms still generate search trees; however, as each problem state can now only label only one search tree node, the search tree is effectively overlaid on the state-space graph whose vertices correspond to problem states and arcs correspond to actions linking pairs of states.
      • Problem states may repeat in the fringe data structure, as states may be encountered several times before they are expanded and added to the closed list.
    • EXAMPLE: Operation of gbBFS in finding a shortest (# edges) path between vertices A and C in a graph. [txt]
    • EXAMPLE: Operation of gbDFS; in finding a path between vertices A and C in a graph. [txt]
    • Performance of a graph-based version of search strategy s
      • Completeness is as in the tree-based version of s.
      • Optimality depends on s.
        • As graph-based search effectively discards all paths to a node but the one found first, it is only optimal if we can gaurantee that the first solution found is the optimal one, e.g., BFS or UCS with all actions having the same cost.
      • Time Complexity: O(#states)
        • This is because each state is expanded at most once and in the worst case, every state in the environment must be expanded; hence, it is the same for every search strategy.
        • In practice, the actual number of generated states is far lower than this worst case.
      • Space Complexity: O(#states)
        • This is because of the closed list.
        • Note that this also applies to tree-based versions that ran in linear space, e.g., DFS and its associated variants.

Thursday, September 25

• Instructor away from campus; lecture cancelled

Monday, September 29

• In-class Exam #1 Notes
  I've finished making up the first in-class exam. The exam will be closed-book and written in-class on paper (please bring your own pens). It will be 75 minutes long and has a total of 50 marks (this is not coincidental; I have tried to make the number of marks for a question times 1 1/2 approximately equivalent to the number of minutes it should take you to do that question). The exam will cover material in course lectures up to and including Lecture #7. There will be three questions:
  1. Topics 1, 2, and 3 (4 parts / 15 marks total)
  2. Topics 2 and 3 (2 parts / 11 marks total)
  3. Topic 3 (3 parts / 24 marks total)

  I hope the above helps, and I wish you all the best of luck with this exam.

Tuesday, September 30

• National Day of Truth and Reconciliation; no lecture

Thursday, October 2 (Lecture #6)
[DC3200, Lecture #5; RN3, Chapter 3; Class Notes]

• Problem Solving and Search (Cont'd)
  • Informed (heuristic) search strategies
    • Uses problem-specific knowledge encoded as heuristic functions that (ideally, but not always) cut down the total number of nodes searched and speed up search times to goal.
      • Heuristic function h(n) gives a (hopefully good) estimate of the cost of the optimal path from node n to a goal node. If n is a goal node, h(n) = 0.
      • h*(n) = perfect heuristic which gives exact cost of optimal path from n to goal node (and wouldn't that be nice ...)
      • EXAMPLE: A heuristic h1(n) for shortest-path in edge-weighted graphs is the cost of the lowest-cost edge originating at n that does not double back to an already-explored node.
      • EXAMPLE: A heuristic h2(n) for shortest-path in 2D grids is the Manhattan distance from n to the the requested location.
      • EXAMPLE: A heuristic h3(n) for efficient plans to make tea is the modified Hamming distiance from the problem state n to a possible goal state.
        • Replace all non-specified items in the goal by * to generate pg and then compute the Hamming distance between the non-star positions in pg and the state encoded in n.
        • For example, given a goal p1 + -p3 + p4 in a five-item state, pg = 1*01* and the modified Hamming distance from pg to sn = 01000 is 2 (position 3 matches and positions 1 and 4 do not match).
      • Types of heuristics
        • An admissible heuristic never overestimates the distance from a node n to a goal node, i.e., h(n) <= h*(n ).
          • Can be seen as an optimistic guess.
          • When h() is admissible, f(n) = g(n) + h(n) never overestimates the cost of a best-possible path from the initial state to a goal state that goes through n.
        • A consistent heuristic (also called a monotone heuristic) has |h(a) - h(b)| <= c(a,b), where c(a,b) is the optimal cost of a path from a to b.
          • With such a heuristic, the difference of the heuristic values of two nodes must be less than or equal to the optimal cost of a path between those nodes.
          • Every consistent heuristic is also admissible; indeed, it is hard (but not impossible) to construct an admissible heuristic that is not consistent.
          • When h(n) is consistent, the values of f(n) = g(n) + h(n) along any path are non-decreasing; this will turn out to be very useful later in our story.
      • EXAMPLE: Which of the heuristics h1(n), h2(n), and h3(n) above are admissible? Which are also consistent?
    • Informed search strategies differ in how they combine g(n) and h(n) to create a function f(n) that is used to select the next node in the open list to expand.
    • Tree-based Greedy Best-First BFS (GBeFS)
      • Select node in open list with lowest f(n) value, where f(n) = h(n), i.e., only cares about distance to goal.
      • Resembles DFS in that it tries a single path all the way to the goal and backs up when it hits a "dead end".
      • EXAMPLE: BFS vs GBeFS in shortest-path in 2D grid world with obstacles. [DC3200, Lecture #5, Slides 19-33 (PDF)]
      • ALGORITHM: Tree-based GBeFS

        1.   Function GBeFS(problem, h(n))
        2.     open = PriorityQueue{f(n) = h(n)}                   <=
        3,     open.add(Node(problem.initial_state))
        f.     while (true)
        5.       if (open.empty) return fail
        6.       node = open.min_f_value()                         <=
        7.       if (node.state is goal) return solution              
        8.       else open.add(Expand(node, problem))
        

        Lines modified from the algorithm for UCS are indicated by "<=".
      • Performance of GBeFS (similar to DFS)
        • GBeFS is not complete
          • May not find goal; may even "get lost" and retrace paths if heuristic is bad.
        • GBeFS is not optimal
        • Time Complexity: O(b^m), where m = maximum explored node depth.
        • Space Complexity: O(bm)
      • Though performance not so great in general, performs well for carefully crafted heuristics; such heuristics can be derived using means-ends analysis.
      • GBeFS was the core search strategy underlying the earliest automated reasoning systems Logic Theorist (1956) (Newell and Simon (1956)) and GPS (General Problem Solver (1959) (Newell, Shaw, and Simon (1959)) as well as foundational computational modeling work on problem solving by humans (Newell and Simon (1972)).
    • Tree-based A* search
      • Most well-known BeFS algorithm.
      • Select node in open list with lowest f(n) value, where f(n) = g(n) + h(n), i.e., cares about total distance from start state to goal.
      • ALGORITHM: Tree-based A* search

        1.   Function A*(problem, h(n))
        2.     open = PriorityQueue{f(n) = g(n) + h(n)}            <=
        3,     open.add(Node(problem.initial_state))
        f.     while (true)
        5.       if (open.empty) return fail
        6.       node = open.min_f_value()                         <=
        7.       if (node.state is goal) return solution
        8.       else open.add(Expand(node, problem))
        

        Lines modified from the algorithm for UCS are indicated by "<=".
      • Performance of Tree-based A*
        • Tree-based A* is complete
          • Will eventually visit all nodes in the search tree, starting with those who h-values are lowest.
        • Tree-based A* is optimal if h(n) is admissible
        • Time Complexity: O(b^m), where m = maximum explored node depth.
        • Space Complexity: O(bm)
    • Graph-based A* search
      • Let us now try to optimize the runtime of A* search by using closed lists.
      • ALGORITHM: Graph-based A* search

        1.   Function gbA*(problem, h(n))
        2.     closed = {}                                         <=
        3.     open = PriorityQueue{f(n) = g(n) + h(n)}            
        4,     open.add(Node(problem.initial_state))
        5.     while (true)
        6.       if (open.empty) return fail
        7.       node = open.min_f_value()                           
        8.       if (node.state is goal) return solution
        9.       if (node.state in closed) continue                <=
        10.      closed.add(note.state)                            <=
        11.      open.add(Expand(node, problem))
        

        Lines modified from the algorithm for tree-based A* search are indicated by "<=".
      • Performance of Graph-based A*
        • Graph-based A* is complete
        • Graph-based A* is optimal if h(n) is consistent
          • Admissible heuristics do not suffice for optimality, as "raw" graph-based search only retains the first-encountered path to a repeated state (where a later-encountered path may be better).
          • If a consistent heuristic is used, the values of f(n) along any path are non-decreasing; as the sequence of nodes expanded by graph-based A* is in non-decreasing order of f(n), any node selected for expansion is on an optimal path as all later nodes are at least as expensive!
        • Time Complexity: O(b^m)
        • Space Complexity: O(b^m)
      • EXAMPLE: (VERY detailed) Graph-based A* search for path between two locations in a 2D grid with obstacles [DC3200, Lecture #5, Slides 68-147 (PDF)]
      • Graph-based A* also has the property that no other optimal uninformed search algorithm can expand fewer nodes; that being said, the number of nodes that need to be searched and retained (as part of the closed list) is still exponential in the worst case and can be prohibitive in practice.
  • There are a variety of ways of improving the performance in practice (though not in the worst case) of the search algorithms above; these ways tend to be specific to particular types of environments, e.g., 2D grids (see DC3200, Lecture #7), or search algorithms, e.g., graph-based A* search (see DC3200, Lecture #5).
  • An important example of the latter is using appropriate data structures to optimize membership query time in open and closed lists in graph-based search. Some common data structures and their worst-case membership query times for an open / closed list with n items are:
    • List /array: O(n)
    • Set / dictionary (via balanced search trees): O(log n)
    • Hash table: O(n)
    • Perfect hash table: O(1)

    Given their simplicity and the possibility of O(1) membership query time, hash tables are typically used.

Tuesday, October 7 (Lecture #7)
[DC3200, Lecture #10; RN3, Chapters 4 and 5; Class Notes]

• Problem Solving and Search (Cont'd)
  • Before we leave the topic of single-agent search, it is worth looking at a class of search methods that are not necessarily complete or optimal but are often used in practice.
  • Local search
    • Useful for problems where the goal state is what is wanted and the path of actions used to create that goal is irrelevant, e.g., combinatorial optimization problems like Maximum Clique:
      Maximum Clique
      Input: A graph G = (V,E).
      Output: A maximum clique of G, i.e., a largest-possible subset V' of V such that each pair of vertices in V' is connected by an edge in G.

    • Assumes a problem state-space where each state s has a "neighbourhood" N(s) of states, each of which are reachable by applying a single action to s.
    • EXAMPLE: The state space for finding the highest point in the St. John's area.
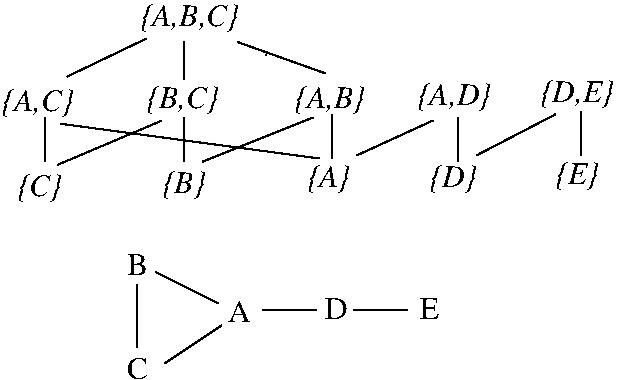
    • EXAMPLE: The state space for the Maximum Clique problem for a graph G.

      

      The state space is the set of all subsets of vertices of G that define clique-subgraphs, e.g., {A,B,C}, {D,E}, {E}. The neighbourhood of a state s is the set of all states corresponding to those vertex-subsets of G that induce clique-subgraphs and that can be created by the addition or removal of a single vertex to or from s, e.g., the neighbourhood of state {B,C} is {{A}, {B}, {A,B,C}}.
    • These neighbourhoods, when combined with a state-evaluation function, induce a state-space landscape (Note that though the discussion and algorithms below are phrased in terms of finding maximum-value states on such landscapes, they can also be rephrased in terms of finding minimum-value states, e.g., (greedy) valley-descending search).
    • EXAMPLE: The state-evaluation function for the St. John's High problem is the elevation of a location above sea level.
    • EXAMPLE: The state-evaluation function for the Maximum Clique problem is the number of vertices bin a clique-state.
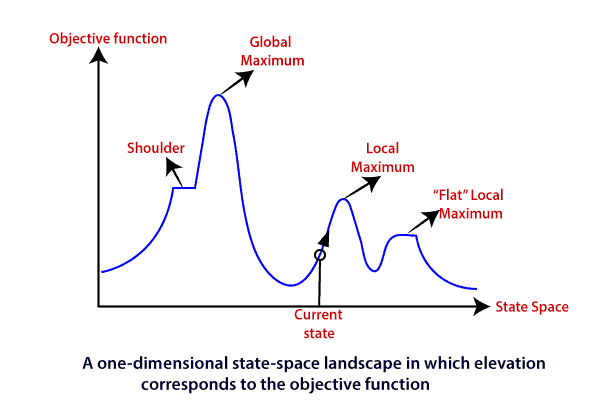
    • EXAMPLE: A generic state-space landscape (RN3, Figure 4.1):
      

      Useful features of such landscapes are:

      • Global maximum: A state with the highest value over all states in the state space.
      • Local maximum: A state with the highest value in that state's neighbourhood.
      • Plateau: A set of adjacent states of the same value. Can distinguish between local maximum plateau (all states adjacent to the plateau have lower value than the states in the plateau) and shoulder plateau (some states adjacent to the plateau have higher value than the states in the plateau).

      Though global maxima are most desirable, local search runs the (frequently unavoidable) risk of being trapped in local maxima.

    • Types of local search are distinguished by the methods used to escape local maxima.
      • Hill-climbing search (greedy search)
        • Starting from some initial state, go "uphill" on the state-space landscape until you cannot go uphill anymore.
        • ALGORITHM: Basic hill-climbing search (RN3, Figuire 4.2)

          1.   Function Hill-Climbing(problem)
          2.     current = Node(problem.initial_state)
          3.     while (true)
          4.       neighbour = highest-value successor of current
          5.       if (neighbour.value <= current.value) return current
          6.       current = neighbour
          

        • This algorithm finds a local maximum, local maximum plateau, or shoulder that is accesible from the initial state.
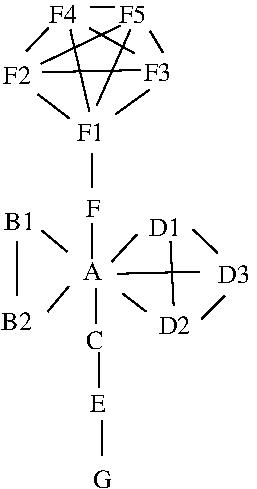
        • EXAMPLE: Basic hill-climbing search for finding (maximal) cliques.

          

          In what ways can hill-climbing search proceed from state {A} in the graph above? State {F}? State {E}? State {D1}?
        • Not complete or optimal in general but is typically fast and very memory-efficient.
          • Is complete and optimal if the state-space landscape has a particular "dome" structure (Cormen et al (2009), Section 16.4), e.g., Prim's and Kruskal's algorithms for finding minimum spanning trees.
        • Variants:
          • Limited sideways-move hill climbing.
            • Allows sideways moves in hopes that an encountered plateau is actually a shoulder.
            • Need to limit the number of sideways moves so you do not go into an infinite loop on an actual plateau.
          • Stochastic hill-climbing.
            • Chooses at random among uphill moves with uphill move probability proportional to degree of solution improvement.
          • First-choice hill-climbing.
            • Chooses at random among uphill moves with uphill move probability proportional to degree of solution improvement until either a move resulting in a state with a value better than that of the current state is found or there are no uphill moves from the current state, i.e., a plateau has been reached..
          • Random-restart hill climbing.
            • Implements common dictum: "If at first you don't succeed, try again."
            • Performs hill-climbing repeatedly from randomly-chosen start states until goal is found.
            • Is complete, as one will eventually generate the goal state.
            • If probability of attaining a goal from a randomly-chosen start state is p, the expected number of required restarts is 1/p.
          • Though all of these variants are slower than basic hill-climbing search, they can be remarkably effective in certain state-space landscapes, e.g. allowing up to 100 sideways moves in a hill-climbing search for the 8-Queens problem increases the percentage of solved instances from 14% to 94%.
      • Local beam search
        • Unlike hill-climbing, which only has one current state, local beam search keeps track of the best k states found so far and performs hill-climbing simultaneously on all of them.
        • EXAMPLE: Basic local beam search for finding (maximal) cliques.
        • Is not equivalent to running k independent random-restart hill-climbing searches in parallel; in local beam search, useful information is passed between searches and resources are focused dynamically where progress is being made, i.e., "No progress there? Help me over here!".
        • Not complete or optimal in general but is typically fast and very memory-efficient.
        • Variants:
          • Stochastic local beam search
            • Chooses k new states at random among uphill moves from the k current states with uphill move probability proportional to degree of solution improvement.
            • Analogous to natural selection in biological evolution.
    • Local search and its variants are characterized by an increasing use of computer time as a substitute for hand-crafted search strategy (Tony Middleton's "cook until done") -- as such, these methods are a first taste of the machine-crafted algorithms we will be looking at in the final lectures of this course.
  • Potential exam questions
  • So far with only looked at search in environments with a single agent; let us now consider search in multi-agent environments.
  • A particularly important (and basic) case of multi-agent environments is two-person board games. These games share a set of properties:
    • Alternating moves, e.g., player 1 moves, then player 2 moves, then player 1 moves, then player 2 moves ...
    • Determinism, i.e., all moves are specified by game rules and there is no randomness.
    • Discreteness of the game environment and game moves.
    • Perfect information, i.e., both players always have complete knowledge of the game state, game rules, and the immediate consequences of all game moves.
    • The games are zero-sum, i.e., any advantage gained by one player is a disadvantage to the other player.
  • How can we design an algorithm to play a two-player alternating-move game?
    1. Manually analyze the game to determine general strategies and tactics, implement the individual strategies and tactics as algorithms, and create a controller which determines which strategy and tactic algorithms are invoked at each point as the game progresses.
       • Corresponds to the way many board games such as chess are taught by and to people.
       • Was the earliest implemented approach; discarded in many cases because it is hideously difficult to do (both in analysis and two-level controler / algorithm architecture).
    2. Implement game controller and strategy / tactic decisions on an individual move basis as a set of IF (game-pattern) THEN (perform move) statements.
       • Transfers implementation difficulty from strategy / tactic / controller design to individual IF-THEN statement design
       • Hideously diffficult to do because even a moderately complex game may require many thousands of IF-THEN statements.
    3. Implement game controller and strategy / tactic decisions on an individual move basis as one-move lookahead and evaluate.
       • At each point in gameplay, look at the moves available to the current player, evaluate the game-states resulting from each of these moves, and pick the move that gives the greatest utility to the current player.
       • Assumes the current player is a rational agent.
       • Assumes a good game-state utility function, which can be very difficult to find.
       • EXAMPLE: Tic-Tac-Toe one-move lookahead and evaluate. [DC3200, Lecture #10, Slide 13 (PDF)]
       • First approach that compactly automates gameplay.
    4. Implement uninformed brute-force search of entire game tree, i.e., one-time full-depth lookahead.
       • Sidestep the difficulty of deriving a good game-state evaluation function by doing a complete game tree search.
       • Starting from the initial state, this game tree has levels that alternate the current player's options at each generated game-state and terminates in game-state leaves in which either player 1 wins, player 2 wins, or (if this is possible in the game) there is a tie.
       • Is gauranteed to find move-sequences that allow players to win; however, it does not gaurantee that both players will necessarily perform the moves specified in the sequence as it makes no assumptions about the rationality of either player.
       • Worse still, as we saw earlier in this course, game trees for even moderately-complex games are VERY large and prohibitively expensive to search completely.
       • EXAMPLE: Total # sequences of actions in some games (game tree complexity)
         • Tic-Tac-Toe: <= 10^5
         • Chess: <= 10^{123}
         • Go: <= 10^{360}
         • Starcraft II: > 10^{1000)
    5. Implement informed partial search of game tree, i.e., succesive limited-depth lookahead and evaluate.
       • Is a compromise between approaches (3) and (4) -- look ahead as far as you can afford to.
       • In this reduced game tree, the current player and the other player are called the max and min players and game-state evaluation is only performed at the leaves of the tree; the results of these evaluations are then propagated backward to the root in alternating minimization and maximization phases until a move is found at the root for the current player that gives the best possible results for them relative to the limited-depth lookahead.
       • Assumes both players are rational agents and that there is a good game-state evaluation function available.
       • EXAMPLE: Limited-depth lookahead and evaluate game tree (one move each player) [DC3200, Lecture #10, Slides 24-29 (PDF)]
       • It is this approach that underlies the popular and widely-used MiniMax AI gameplay algorithm.

Thursday, October 9

• In-class Exam #1

Tuesday, October 14

• Midterm break; no lecture

Thursday, October 16

• Instructor away from campus; lecture cancelled

Tuesday, October 21 (Lecture #8)
[DC3200, Lecture #10; RN3, Chapter 5; Class Notes]

• Went over In-class exam # 1.
• Problem Solving and Search (Cont'd)
  • We will build up the basic limited-depth MiniMax algorithm in the following stages.
  • ALGORITHM: MaxValue (one-level)

    1.   Function MaxValue(s)
    2.     v = -infinity
    3.     for (c in children(s))
    4.       v' = eval(c)
    5.       if (v' > v) v = v'
    6.     return v
    

  • ALGORITHM: MaxValue (full tree)

    1.   Function MaxValue(s)
    2.     if leaf(s)                  <=
    3.       return eval(s)            <=
    4.     v = -infinity
    5.     for (c in children(s))
    6.       v' = MinValue(c)          <=
    7.       if (v' > v) v = v'
    8.     return v
    

    Lines modified from the MaxValue (one-level) algorithm are indicated by "<=".
  • ALGORITHM: MaxValue and MinValue (full tree)

    1.   Function MaxValue(s)         Function MinValue(s)
    2.     if leaf(s)                   if leaf(s)
    3.       return eval(s)               return eval(s)
    4.     v = -infinity               v = +infinity
    5.     for (c in children(s))      for (c in children(s))
    6.       v' = MinValue(c)            v' = MaxValue(s)         
    7.       if (v' > v) v = v'          if (v' < v) v = v'
    8.     return v                    return v 
    
         Initial Call: MaxValue(startState)
    

    eval(s) returns score wrt the current (maximizing) player.
  • ALGORITHM: MaxValue and MinValue (limited-depth)

    1.   Function MaxValue(s, d)     Function MinValue(s, d)       <=
    2.     if (leaf(s) or d >= MaxD)    if (leaf(s) or d >= MaxD)    <=
    3.       return eval(s)               return eval(s)
    4.     v = -infinity               v = +infinity
    5.     for (c in children(s))      for (c in children(s))
    6.       v' = MinValue(c, d+1)       v' = MaxValue(c, d+1)     <=  
    7.       if (v' > v) v = v'          if (v' < v) v = v'
    8.     return v                    return v 
    
         Initial Call: MaxValue(startState, 0)
    

    Lines modified from the MaxValue and MinValue (full tree) algorithms are indicated by "<=".
  • ALGORITHM: MiniMax search (depth-limited)

    1.   Function MiniMax(s, d, isMax)
    2.     if (leaf(s) or d >= MaxD)
    3.       return eval(s)       
    4.     if (isMax)
    5.       v = -infinity         
    6.       for (c in children(s))
    7.         v = max(v, MiniMax(c, d+1, false))
    8.     else
    9.       v = +infinity         
    10.      for (c in children(s))
    11.        v = min(v, MiniMax(c, d+1, true))
    12.    return v             
    
           Initial call: MiniMax(startState, 0, true)
    

  • One final (and trivial) change is required to ensure that the best action for the current (max) player to take is stored in the start state.
  • ALGORITHM: MiniMax search (depth-limited) + saved best action [ASSIGNMENT #2]

    1.   Function MiniMax(s, d, isMax)
    2.     if (leaf(s) or d >= MaxD)
    3.       return eval(s)       
    4.     if (isMax)
    5.       v = -infinity         
    6.       for (c in children(s))
    7.         v' = MiniMax(c, d+1, false)                       <=
    8.         if (v' > v)                                       <=
    9.           v = v'                                          <=
    10.          if (d == 0) self.currentBestAction = c.action   <=
    11.    else
    12.      v = +infinity         
    13.      for (c in children(s))
    14.        v = min(v, MiniMax(c, d+1, true))
    15.    return v             
    
           Initial call: MiniMax(startState, 0, true)
    

    • INTERLUDE: A look at the mechanics of Assignment #2.
    • EXAMPLE: MiniMax generation and evaluation of an altNim game tree from Assignment #2 (maxD = 2, i.e., two-move lookahead / startOdd = True / # given sticks = 6) (see Test #3 in Assignment #2).
      

    • EXAMPLE: MiniMax generation and evaluation of an altNim game tree from Assignment #2 (maxD = 3, i.e., three-move lookahead / startOdd = False / # given sticks = 15) (see Test #6 in Assignment #2).
      

Thursday, October 23

• Instructor ill; no lecture

Tuesday, October 28 (Lecture #9)
[DC3200, Lecture #10; RN3, Chapters 5 and 6; Class Notes]

• Problem Solving and Search (Cont'd)
  • Given that max(a, b) = -max(-a, -b), we can shorten the MiniMax algorithm above to create the NegaMax algorithm.
  • NegaMax is harder to understand and debug but it is the version of MiniMax that is used in practice.
  • ALGORITHM: NegaMax search (depth-limited)

    1.   Function NegaMax(s, d, isMax)
    2.     if (leaf(s) or d >= MaxD)
    3.       return eval(s)       
    5.     v = -infinity         
    6.     for (c in children(s))
    7.       v = max(v, -NegaMax(c, d+1, false))
    12.    return v             
    
           Initial call: NegaMax(startState, 0, true)
    

  • Performance of MiniMax search
    • MiniMax is complete wrt given maximum depth MaxD
    • MiniMax is optimal wrt given maximum depth MaxD
    • Time Complexity: O(b^{MaxD})
    • Space Complexity: O(b * MaxD)
    • MiniMax plays the Nash Equilibrium, i.e., each player makes the best response to the possible actions of the other player and thus neither player can gain by deviating from the moves proposed by MiniMax.
  • A closer examination of the intermediate results created at the internal game tree nodes during MiniMax search reveals that these results can be used to prune parts of the game tree that cannot yield solutions better than those that have been found so far.
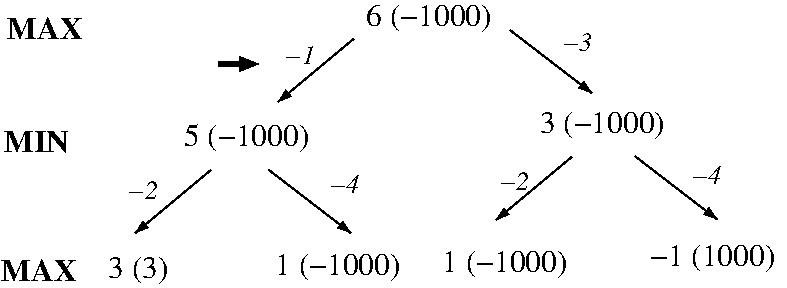
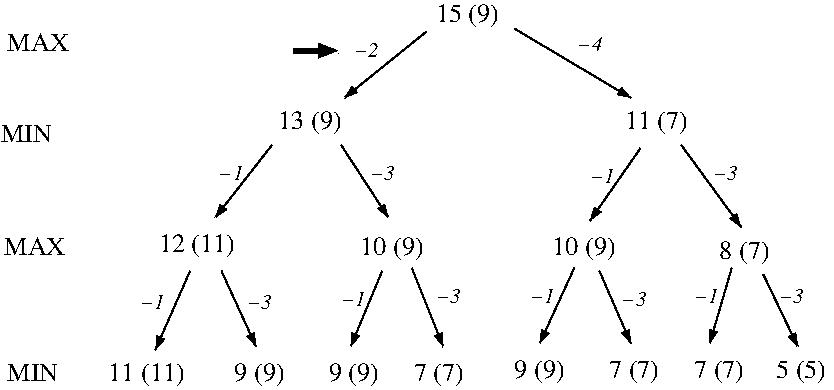
  • EXAMPLE: MiniMax + pruning (one move each player) [DC3200, Lecture #10, Slides 40-50 (PDF)]
  • This optimization of MiniMax is known as AlphaBeta pruning.
    • Introduces two new MiniMax parameters:
      • alpha: Best alternative for the Max player on this particular path through the game tree.
      • beta: Best alternative for the Min player on this particular path through the game tree.
    • The interval [alpha, beta] is an ever-narowing window as MiniMax search progresses which ``good'' paths must pass through and thus allows other paths to be pruned.
  • ALGORITHM: MaxValue and MinValue (limited-depth + AlphaBeta)

    1.   Function MaxValue(s, a, b, d)     Function MinValue(s, a, b, d)    <=
    2.     if (leaf(s) or d >= MaxD)          if (leaf(s) or d >= MaxD)    
    3.       return eval(s)                    return eval(s)
    4.     v = -infinity                     v = +infinity
    5.     for (c in children(s))            for (c in children(s))
    6.       v' = MinValue(c, a, b, d+1)       v' = MaxValue(c, a, b, d+1)  <=
    7.       if (v' > v) v = v'                if (v' < v) v = v'
    8.       if (v' >= b) return v             if (v' <= a) return v        <=
    9.       if (v' > a) a = vi                if (v' < b) b = v'           <=
    10.    return v                          return v 
    
         Initial Call: MaxValue(startState, -infinity, +infinity, 0)
    

    Lines modified from the MaxValue and MinValue (limited-depth) algorithms are indicated by "<=".
  • EXAMPLE: MaxValue + AlphaBeta pruning (two moves each player) [DC3200, Lecture #10, Slides 56-110 (PDF)]
  • ALGORITHM: MiniMax search (depth-limited + AlphaBeta)

    1.   Function MiniMax(s, a, b, d, isMax)                   <=
    2.     if (leaf(s) or d >= MaxD)
    3.       return eval(s)       
    4.     if (isMax)
    5.       v = -infinity         
    6.       for (c in children(s))
    7.         v' = max(v, MiniMax(c, a, b, d+1, false))       <=
    8.         if (v' > v) v = v'                              <=
    9.         if (v' > b) return v                            <=
    10.        if (v' > a) a = v'                              <=
    11.    else
    12.      v = +infinity         
    13.      for (c in children(s))
    14.        v' = min(v, MiniMax(c, a, b, d+1, true))        <=
    15.        if (v' < v) v = v'                              <=
    16.        if (v' <= a) return v                           <=
    17.        if (v' < b) b = v'                              <=
    18.    return v             
    
           Initial call: MiniMax(startState, -infinity, +infinity, 0, true)
    

    Lines modified from the MiniMax (limited-depth) algorithm are indicated by "<=".
  • One final (and trivial) change is required to ensure that the best action for the current (max) player to take is stored in the start state.
  • ALGORITHM: MiniMax search (depth-limited + AlphaBeta + saved best action)

    1.   Function MiniMax(s, a, b, d, isMax)                     
    2.     if (leaf(s) or d >= MaxD)
    3.       return eval(s)       
    4.     if (isMax)
    5.       v = -infinity         
    6.       for (c in children(s))
    7.         v' = max(v, MiniMax(c, a, b, d+1, false))           
    8.         if (v' > v) v = v'                                  
    9.         if (v' > b) return v                                
    10.        if (v' > a)                                       <=
    11.          a = v                                           <=
    12.          if (d == 0) self.currentBestAction = c.action   <=
    13.    else
    14.      v = +infinity         
    15.      for (c in children(s))
    16.        v' = min(v, MiniMax(c, a, b, d+1, true))          
    17.        if (v' < v) v = v'                                
    18.        if (v' <= a) return v                             
    19.        if (v' < b) b = v'                                
    20.    return v             
    
           Initial call: MiniMax(startState, -infinity, +infinity, 0, true)
    

    Lines modified from the MiniMax (limited-depth + AlphaBeta) algorithm are indicated by "<=".
  • AlphaBeta pruning cuts the number of nodes searched by MiniMax from O(b^d) to approximately 2b^{d/2} (which can be proven to be the best possible). This allows searches to depth d under MiniMax with a fixed amount of computational resources to go to depth 2d under MiniMax + AlphaBeta with the same resources, e.g., a previously bad gameplaying program can be enhanced to beat a human world champion!
  • The MiniMax + AlphaBeta algorithm can be shortened by rearranging the code above to be more efficient; a runtime limit can also be enforced by using the iterative deepening strrategy previously applied to Depth-First Search in Lecture #5 (see Lecture #10 of DC3200 for details).
• Potential exam questions
  • In most of our our previously discussed search algorithms (cf. local search), our primary concern when solving problems was more with sequences of actions that resulted in goal states rather than the goal states themselves.
  • Are there other types of search algorithms for problems where the goal states are the primary concern?
  • Let us focus on Constraint Satisfaction Problems (CSPs).
    • In a CSP, states have factored representations (see Lecture #3) that are defined by a set of variables X = {X1, X2, ..., Xn}, each of which has a value from some variable-specific domain Di, and a set C of constraints on the values of those variables.
      • A constraint is described by a pair <(scope), rel> where scope is a tuple of variables from X and rel is a relation specifying the values of the variables in rel allowed by the constraint.
      • The number or variables in scope determines that constraint's arity (e.g., 1 = unary, 2 = binary, 3 = trinary, m = m-ary where m is arbitrary (global constraint)).
      • There are typically several ways to specify a particular variable relation.
      • EXAMPLE: We can specify the binary constraint on variables X1 and X2 with common domain {A,B} that X1 and X2 have different values as <(X1,X2),[(A,B),(B,A)]> or <(X1,X2), X1 \neq X2>.
    • Each state in the state-space of a CSP specifies an assignment of values [X1 = v1, X2 = v2, ..., Xn = vn] to the variables in the CSP.
      • A value-assignment that gives a value to each variable in a CSP is said to be complete; if one or more variables are not assigned values, the value-assignment is partial.
      • A value-assignment that satisfies all given constraints in C for a CSP is said to be consistent; if one or more constraints in C are not satisfed, the value-assignment is inconsistent..
    • A solution (goal state) for a CSP is a complete consistent value-assignment for that CSP.
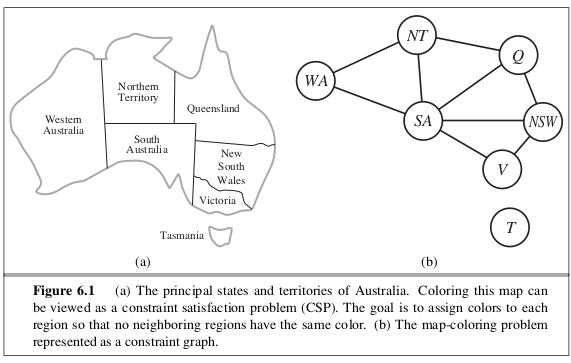
    • EXAMPLE: A CSP for coloring a map of Australia.
      
      • In map coloring, we want to assign colors to the regions in the map such that no two adjacent regions have the same color.
      • Coloring a map of Australia (part (a)) can be modeled as a CSP with variables X = {WA, NT, Q, NSW, V, SA, T} over the common domain D = {red, green, blue} and the binary constraints C = {SA \neq WA, SA \neq NT, SA \neq Q, SA \neq NSW, SA \neq V, WA \neq NT, NT \neq Q, Q \neq NSW, NSW \neq V} (where X \neq Y is shorthand for the constraint <(X,Y) X \neq Y>)..
      • Such a CSP with all binary constraints can be modeled as a constraint graph (part (b)), which is an undirected graph whose vertices correspond to variables and edges correspond to constraints.
        • CSPs with m-ary constraints, m >= 2, can be modeled as constraint hypergraphs (See RN3, Figure 6.2).
      • There are many possible solutions for the map coloring CSP above, e.g., [WA = red, NT = green, Q = red, NSW = green, V = red, SA = blue, T = red].
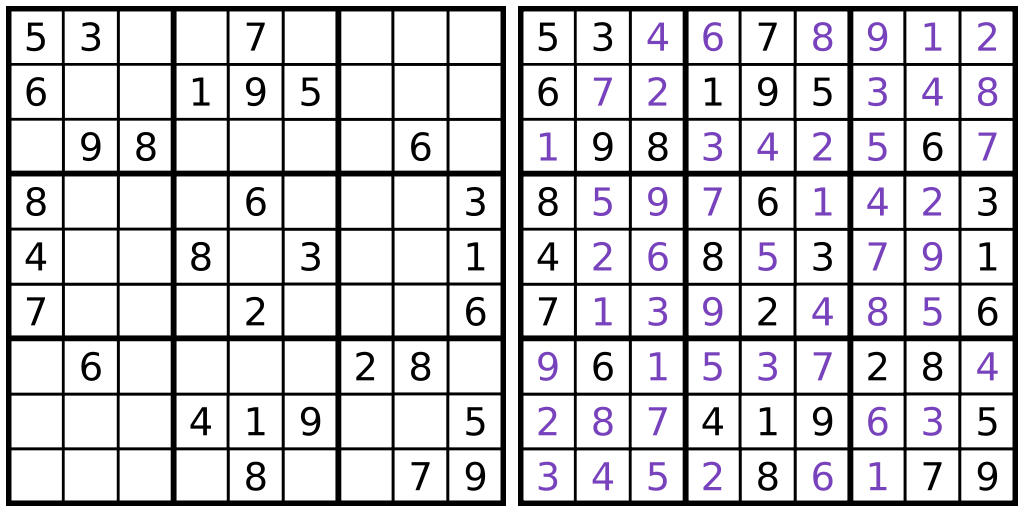
    • EXAMPLE: Soduku
      
      • In soduku, one is a given a partial assignment from the domain {1, 2, ..., 9} to the squares of a 9 x 9 grid (left) and we want to fill in the unassigned squares such that no number appears twice in any column, row, or 3 x 3 box (right).
      • A CSP for a game of soduku corresponds to a set X of 81 variables (one for each square in the 9 x 9 grid) over the common domain D = {1, 2, ..., 9}, a given partial value-assignment to X wrt D (i.e., the initially specified square-numbers), and a set C of 9 + 9 + 9 = 27 global constraints specifying that the values of the 9 variables in each column, row, and 3 x 3 box are different, e.g., AllDiff(A1, A2, A3, A4, A5, A6, A7, A8, A9) for the first row in the 9 x 9 grid.
    • One way of solving a CSP is to generate and evaluate all possible value-assignments for that CSP's variables.
      • This can be done in a tree with depth d = |X| and branching factor b = max |Di|, where each level assigns values to a particular variable and each leaf encodes a complete assignment to the variables in X.
      • This tree presupposes fixed orders on both the variables on X and the values in each domain Di.
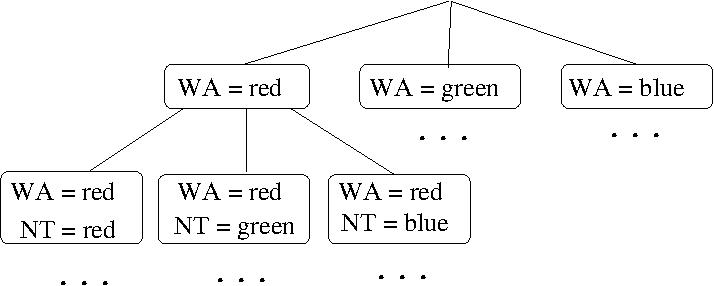
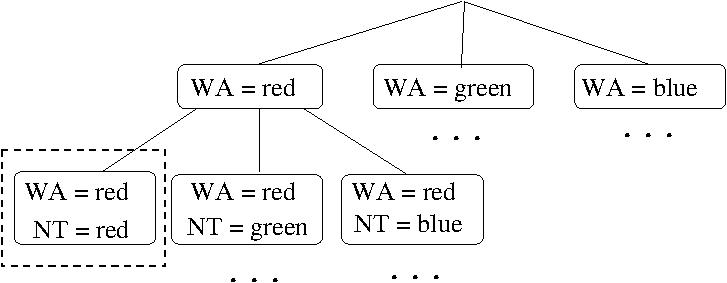
    • EXAMPLE: A portion of a complete CSP value-assignment tree for colouring a map of Australia:
      

    • Generating complete value-assignment trees is memory-expensive as such trees can have b^{d + 1} - 1 nodes; can lower memory requirements by using Depth-First Search to generate leaves one at a time.
    • ALGORITHM: CSP DFS (RN3, Figure 6.5 variant)

      1.   Function CSP_Search(csp)
      2.     return CSP_DFS({}, 1, csp)
      
      3.   Function CSP_DFS(assignment, d, csp)
      4.     if (depth d = |X| + 1, i.e., assignment is complete, and
                 assignment is consistent) 
      5.       return assignment
      6.     else
      7.       var = Xd
      8.       for each value in Dd
      9.         add {Xd = value} to assignment
      10.        result = CSP_DFS(assignment, d + 1, csp)
      11.        if (result \neq failure)
      12.          return result
      12.        remove {Xd = value} from assignment
      13.    return failure
      

    • The above fixes the memory problem but it is still time-expensive as we may generate up to b^{d + 1} - 1 nodes in the worst case. Indeed, the NP-completeness of many CSP problems suggests that such brute-force algorithms may be the best we can do if we want to solve all input instances of such CSPs.
    • ... But we typically don't want to solve all instances of a particular CSP problem, only the ones we encounter in practice -- can we do better in practice?

Thursday, October 30 (Lecture #10)
[RN3, Chapters 6 and 7; Class Notes]

• Problem Solving and Search (Cont'd)
  • Constraint Satisfaction Problems (CSPs) (Cont'd)
    • Let's start by unpacking the constraints from leaf-evaluation.
      • Observe that if a partial assignment does not satisfy some constraint ci in C, no completion of this partial assignment can satisfy ci. Hence, we can stop search at any node whose partial assignment is inconsistent with some constraint in C and thus prune the subtree rooted at that node.
      • ALGORITHM: CSP DFS + Partial (RN3, Figure 6.5 variant)

        1.   Function CSP_Search(csp)
        2.     return CSP_DFS2({}, 1, csp)
        
        3.   Function CSP_DFS2(assignment, d, csp)
        4.     if (depth d = |X| + 1, i.e., assignment is complete)    <=
        5.       return assignment
        6.     else
        7.       var = Xd
        8.       for each value in Dd
        9.         if (value is consistent with assignment)          <=
        10.          add {Xd = value} to assignment
        11.          result = CSP_DFS2(assignment, d + 1, csp)
        12.          if (result \neq failure)
        13.            return result
        14.          remove {Xd = value} from assignment
        15.    return failure
        

        Lines modified from the algorithm CSP DFS are indicated by "<=".

      • EXAMPLE: A portion of a CSP value-assignment tree for colouring a map of Australia which allows pruning of inconsistent partial assignment subtrees (dashed box):
        

    • Further improvements arise from dynamic variable / domain-value ordering heuristics.
      • Variables can be ordered by the minimum-remaining value (MRV) or degree heuristics, which respectively prefer the variables with the most constrained domains and the variables that are involved in the largest number of constraints, e.g., choose SA first in coloring a map of Australia.
      • Domain values can be ordered by the least-constraining heuristic, which prefers values that rule out the fewest choices for neighbouring values in the constraint graph and thus allows maximum flexibility for future value-choices.
      • Good variable-ordering heuristics prune the largest parts of search trees quickest (fail-first) while good domain-value ordering heuristics consider first those values most likely to lead to solutions (fail-last).
      • ALGORITHM: CSP DFS + Partial + Ordering (RN3, Figure 6.5 variant)

        1.   Function CSP_Search(csp)
        2.     return CSP_DFS3({}, csp)
        
        3.   Function CSP_DFS3(assignment, csp)
        4.     if (assignment is complete) 
        5.       return assignment
        6.     else
        7.       var = selectUnassignedVariable(csp, assignment)            <=
        8.       for each value in orderDomainValues(var, assignment, csp)  <=
        9.         if (value is consistent with assignment)
        10.          add {var = value} to assignment
        11.          result = CSP_DFS3(assignment, csp)
        12.          if (result \neq failure)
        13.            return result
        14.          remove {var = value} from assignment
        15.    return failure
        

        Lines modified from the algorithm CSP DFS + Partial are indicated by "<=".

    • We can also make inferences over the constraints themselves (constraint propagation) to derive useful domain restrictions for variables.
      • Such constraint consistency checks can involve one or more constraints of varying constraint arities.
        • Enforcing constraints that a variable has a particular value (unary consistency), e.g., the constraint <(SA) SA = red> that the SA region of the map of Australia must be colored red.
        • Enforcing constraints on pairs of variables (arc consistency) such that every value in a variable's domain can satisfy all binary constraints containing that variable, e.g., the constraint <(WA,NT) WA \neq NT> is satisfied by picking any color for WA and not picking the same color for NT.
        • Enforcing (sets of) constraints on 3 variables (path consistency), e.g., WA, NT, and SA are pairwise linked by difference constraints and hence must have three different colors.
      • Constraint propagation typically reduces the sizes of variable domains; if in this process any variable domain becomes empty, at least one of the type of constraints being checked cannot be satisfied by any assignment of values to the variables in the CSP.
      • ALGORITHM: AC-3 for arc consistency (RN3, Figure 6.3)

        1.   Function AC-3(csp)
        2.     q = queue({arcs in csp})
        3.     while (q is not empty)
        4.       (Xi, Xj) = q.pop()
        5.       if revise(csp, Xi, Xj)
        6.         if (|Di| = 0) return false
        7.         for (each Xk \neq Xj that is a neighbour of Xi)
        8.           q.add((Xk, Xi))
        9.     return true
        
        10.  Function revise(csp, Xi, Xj)
        11.    revised = false
        12.    for (each vi in Di)
        13.      if (no value vj in Dj allows (vi,vj) to satisfy
                      the constraint between Xi and Xj in csp)
        14.        delete vi from Di
        15.        revised - true
        16.    return revised
        

      • In the best case, constraint propagation derives solutions and replaces search, e.g., constraint propagation algorithm for map 2-coloring; however, it is more commonly done as preprocessing for and subsequent interleaving with search.
      • ALGORITHM: CSP DFS + Partial + Ordering + Inference (RN3, Figure 6.5)

        1.   Function CSP_Search(csp)
        2.     return CSP_DFS4({}, csp)
        
        3.   Function CSP_DFS4(assignment, csp)
        4.     if (assignment is complete) 
        5.       return assignment
        6.     else
        7.       var = selectUnassignedVariable(csp, assignment)
        8.       for each value in orderDomainValues(var, assignment, csp)
        9.         if (value is consistent with assignment)
        10.          add {var = value} to assignment
        11.          inferences = getInferences(csp, var, assignment)       <=
        12.          if (inferences \neq failure)                           <=
        13.            add inferences to assignment                         <=
        14.            result = CSP_DFS4(assignment, csp)
        15.            if (result \neq failure)
        16.              return result
        1r.        remove {var = value} and inferences from assignment      <=
        18.    return failure
        

        Lines modified from the algorithm CSP DFS + Partial + Ordering are indicated by "<=".

    • More complex algorithm enhancements yield further improvements in performance, e.g., intelligent backtracking (backjumping).
    • Local search may also be done with respect to CSPs, using a state-space landscape based on complete assignments where states are adjacent if they differ in a single variable assignment and the state evaluation function is the number of constraints in C that are not satisfied by the assignment encoded in that state.
    • ALGORITHM: MinConflicts (RN3, Figure 6.8)

      1.   Function minConflicts(csp, maxSteps)
      2.     current = an initial complete assignment for csp
      3.     for i = 1 to maxsteps do
      4.       if current is consistent return current
      5.         var = a randomly-chosen conflicted variable from X
      6.         value = the value v for var that minimizes
                          conflicts(var, v, current, csp)
      7.         set var = v in current
      8.     return failure
      
         conflicts(var, v, current, csp) returns the number of constraints
          in csp that would be violated by setting var to v in current
      

    • Min-conflicts is surprisingly effective for many CSPs. For example, the run-time of Min-conflicts on the n-Queens problem is independent of problem size such that the million-Queens problem is solved in an average of 50 steps!
• Potential exam questions
• Logical Reasoning
  • Use richer representations of knowledge to go from domain-specific search procedures to domain-general search procedures. Here we will focus on knowledge representations based on various logics.
  • Knowledge-based agents
    • knowledge base (KB) = set of (true) sentences.
    • Interact with KB by TELL and ASK operations, both of which may involve inference, i.e., creating new sentences from old.
      • Inference obeys the requirement that any new sentences that are derived must follow (in a technical sense we will discuss later) from one or more of the sentences known from previous TELL interactions or inferences.
    • ALGORITHM: Knowledge-based agent percept->action computations (RN3, Figure 7.1)

      1.   Function KB-Agent(KB, t, percept)
      2.     TELL(KB, makePerceptSentence(percept, t))
      3.     action = ASK(KB, makeActionQuery(t))
      4.     TELL(KB, makeActionSentence(action, t))
      5.     t = t + 1
      6.     return action
      

    • A KB initially encodes only background knowledge, and is enriched both by percepts obtained during agent interaction with the environment and inference over that KB. As such, KB are often described at the knowledge level, i.e., what is known and inferred, rather than the implementation level, i.e., how what is known is physically represented.
    • An agent's behavior can be derived purely from a KB, percepts, and inference (declarative approach) or from hard-coded behaviors (procedural approach).
      • Successful agents often combine these approaches, using declarative knowledge for generality and compiling this knowledge into procedural code when necessary for efficiency.
  • EXAMPLE: Wumpus World (RN3, Figure 7.2)

    

    • Wumpus World (WW) is a puzzle game in which an agent must explore a cave to find and return a cache of gold while avoiding bottomless pits and the deadly wumpus.
    • The WW problem is described as follows:
      • Environment: A 4 x 4 square containing one wumpus, one cache of gold, and several bottomless pits. The agent always starts at square [1,1] facing right and initially has no knowledge of the environment except that agent's percept at [1,1].
      • Sensors: An agent has five one-bit sensors:
        1. Stench: Returns True if the wumpus (alive or dead) is in same square as the agent or is in a square directly (not diagonally) adjacent to the agent.
        2. Breeze: Returns True if the agent is directly adjacent to a bottomless pit.
        3. Glitter: Returns True if the agent is in the same square as the cache of gold.
        4. Bump: Returns True if the agent walks into one of the four walls surrounding the grid.
        5. Scream: Returns True if the wumpus dies after being struck by an arrow (see below).
        A percept will be given as a binary vector of the current values for these sensors. For example, if there is a stench and a breeze but no glitter, bump or scream, the percept will be [S,B,-,-,-].
      • Actuators: The agent can perform the following actions:
        • The agent can move forward one square (Forward), turn left 90 o (TurnLeft), or turn right 90 o (TurnRight).
          • If a move forward would cause an agent to bump into a wall, the agent does not move.
          • If an agent enters a square with a live wumpus or a bottomless pit, the agent suffers a horrible death.
        • The agent can Shoot its only arrow forward in the direction the agent is facing.
          • The arrow travels in that direction until it either hits the wumpus (and kills it) or strikes a wall.
        • If the agent is in the same square as the cache of gold, the agent can Grab the cache.
        • If the agent is on square [1,1], it can Climb out of the cave.
      • Performance Measure: +1000 for climbing out of the cave with the gold, -1000 for falling into a bottomless pit or being eaten by the wumpus, -10 for shooting the arrow, and -1 for each other action.

      The game ends when the agent dies or climbs out of the cave. Note that even if an agent lives, it may not be successful, e.g., the cache of gold may be surrounded by bottomless pits and hence inaccessible.

    • The main challenge to an agent in WW is that agent's initial ignorance of the configuration of the environment; this ignorance is incrementally dispelled by reasoning-guided exploration, e.g.,
      1. In [1,1], percept is [-,-,-,-,-]; squares [1,2] and [2,1] are OK to move into => move to square [2,1].
      2. In square [2,1], percept is [-,B,-,-,-]; squares [2,2] and [3,1] may have bottomless pits => move back to [1,1] and then to [1,2].
      3. In [1,2], percept is [S,-,-,-,-]; the wumpus cannot be in [2,2] (as stench would have been perceived when visiting [2,1]) so the wumpus is in [1,3] and [2,2] is OK => move to square [2,2].
      4. In [2,2], percept is [-,-,-,-,-]; squares [2,3] and [3,2] are OK => move to square [2,3].
      5. In [2,3], percept is [S,B,G,-,-]; the cache of gold is in this square => grab cache of gold, retrace path to [1,1] on OK squares, and climb out of the cave.

      Several of the inferences made above, e.g., in (3), are difficult because they involve knowledge gained at different times and in different places.

    • Note that when the agent draws a conclusion from available information, that conclusion is only guaranteed to be correct if the available information is correct. Hence, it is critical that sensors return correct values and actuators correctly and completely perform requested actions.

Tuesday, November 4 (Lecture #11)
[RN3, Chapter 7; Class Notes]

• Logical reasoning (Cont'd)
  • Logic: An Overview
    • Each logic has an associated syntax and semantics, where the syntax specifies all well-formed sentences in that logic and the semantics specifies whether or not each well-formed sentence in that logic is true with respect to each possible world (or, more formally, model).
      • A possible world is a (potentially) real world one or more agents exist within, while a model is a mathematical abstraction which fixes the truth or falsity of every relevant sentence relative to variable-values proposed by that model.
      • If a sentence s is true in a model m, we say that m satisfies s or m is a model of s.
      • EXAMPLE: A possible world consists of x men and y women sitting at a table playing bridge; as a game of bridge requires exactly 4 players, the sentence s = "x + y = 4" must be true. Formally, all possible models for this world are the assignments of non-negative integers to x and y and the models that satisfy, s are those that assign values to x and y that add to 4, e.g., [x = 1 / y = 3], [x= 4 / y = 0].
    • Given a definition of truth, we can now define logical reasoning / inference as the process of correctly deriving a conclusion s from a body of knowledge KB (KB |-i s).
      • a |= b means that sentence a entails sentence b, i.e., b follows from a.
      • More formally, a |= b if and only if M(a) \subseteq M(b), i.e., in every model for which a is true, b is also true.
      • Given this definition of entailment, logical inference is the process of deriving a valid conclusion s from a knowledge base KB (sometimes written as KB |-i s).
      • Think of all consequences of KB as a haystack and a particular consequence s as a needle. Entailment can say whether or not a specified needle is in a haystack, and inference is the finding of that needle.
    • Model checking is an inference procedure that enumerates all possible worlds and for a sentence s checks if s is true in all models for which KB is true; as such, it shows one way in which entailment can be used to derive conclusions.
    • EXAMPLE: Model checking for Wumpus World (RN3, Figure 7.5)
      • Let KB be the KB at the beginning of step (2) in the reasoning-based exploration of WW above. Relative to KB, consider the following two sentences:
        • a1 = "There is no pit in [1,2]".
        • a2 = "There is no pit in [2,2]".

        

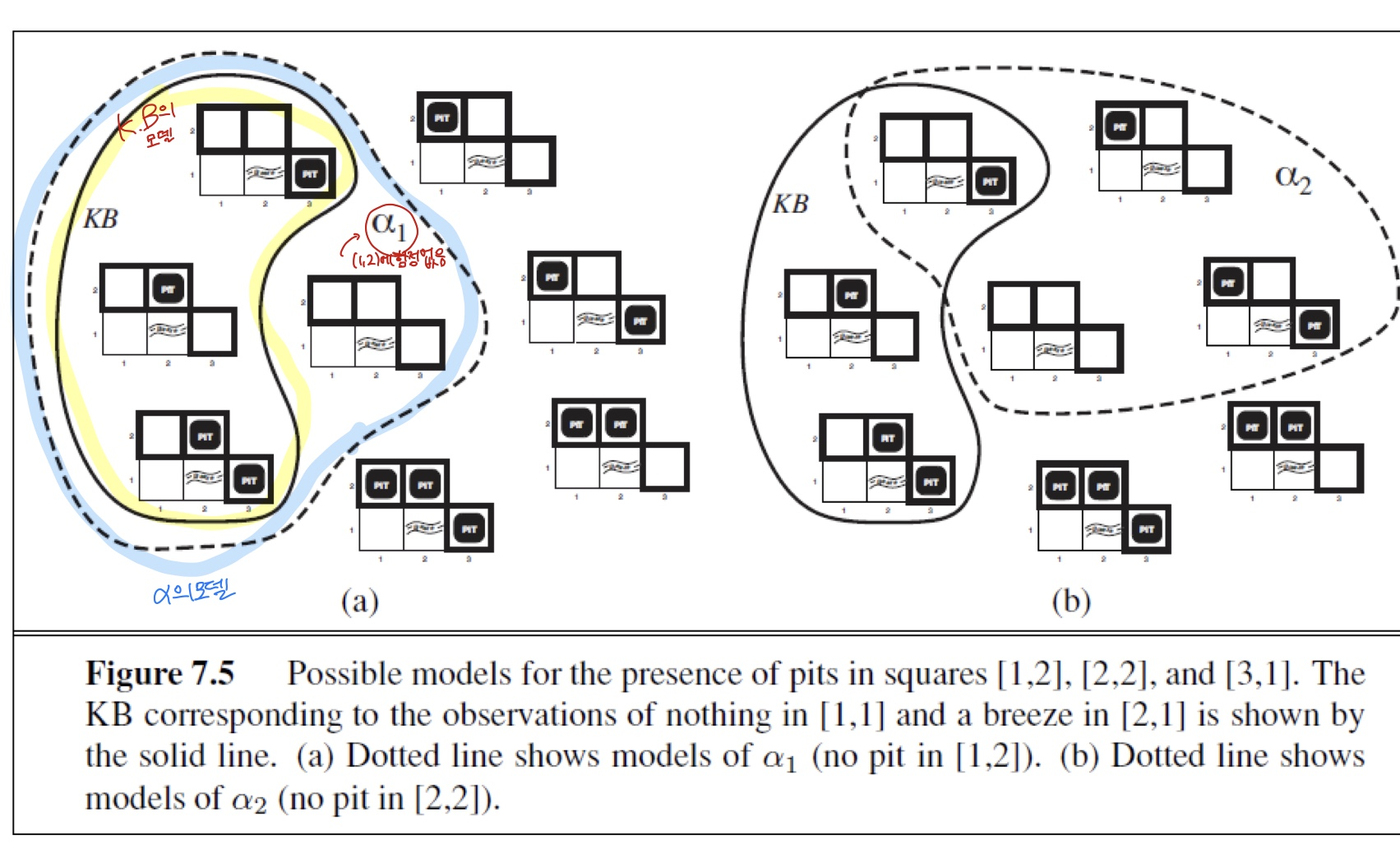
      • From inspection, we can see that for every model in which KB is true, a1 is also true and hence KB |= a1. However, we can also see that in some models in which KB is true, a2 is false, i.e., KB |\= a2. Hence we can conclude that there is a no pit in [1,2] but we cannot conclude that there is not (or, for that matter, is) a pit in [2,2].
    • Desirable properties of inference algorithms:
      • Soundness (Truth-preserving); An inference algorithm that only derives entailed conclusions is sound, i.e., the inference algorithm does not make up things.
      • Completeness: An inference procedure that can derive any conclusion that is entailed is complete, i.e., it is not the case that there are entailed conclusions that the inference algorithm cannot derive.
    • Logical reasoning should also be grounded in the real world, i.e., if s is derived from a KB by a sound inference procedure then s should be true in the real world. One does this by making sure sensors and actuators are correct (grounded percepts) and taking care in grounding inference rules in the real world.
  • Propositional logic (PL)
    • Syntax
      • Sentences in PL can be atomic sentences consisting of a single Boolean literal, i.e., True, False, or propositional symbol, e.g., P, Q, R, or complex sentences built up using logical connectives, e.g., not, and, or, => (implies), <=> (if and only if), and parentheses.
        • Though there is a precedence order on logical connectives, it is perhaps best to use parentheses to denote the wanted recursive structure of complex sentences.
      • Syntax of PL (RN3, Figure 7.7)
        
    • Semantics
      • The truth value of a sentence s in PL for a given model M is built up recursively in a bottom-up fashion from the truth-values of the propositional symbols in s wrt M by applying the truth tables for the logical connectives in s, e.g.,

        

        The truth table for => is counterintuitive because P => Q (unlike natural language "if P then Q") does not imply causation or relevance between P and Q, e.g., "5 is odd => Tokyo is the capital of Japan" is true in PL. Rather, P => Q should be interpreted as "If P is true then I am claiming Q is true; otherwise, I am making no claim".

    • EXAMPLE: A PL KB for Wumpus World
      • Focus for now on the immutable aspects of WW. This will be done for each location [x,y] in the cave with the following symbols:
        • Pxy: True if there is a pit in [x,y].
        • Wxy: True if there is a wumpus (dead or alive) in [x,y].
        • Bxy: True if the agent perceives a breeze in [x,y].
        • Sxy: True if the agent perceives a stench in [x,y].
      • The following sentences will suffice to derive not P12 (there is no pit in [1,2]):
        • R1: not P11 (there is no pit in [1,1])
        • R2: B11 <=> (P12 or P21)
        • R3: B21 <=> (P11 or P22 or P31)
        • R4: not B11
        • R5: B12
    • PL Inference procedures
      • Given a knowledge base KB and a sentence s in in PL, we want to determine if KB |= s, e,g, for the WW KB, is it the case that KB |= not P12?
      • We will here consider two broad classes of inference procedures: model checking and theorem proving.
      • Model checking
        • Basic model checking
          • Given a set S of relevant propositional symbols, for all possible truth-assignments to the symbols in S, i.e., all possible models for S, check that s is true for every truth-assignment for which KB is true.
          • ALGORITHM: TT-Entails? (RN3, Figure 7.10)

            1.   Function TT-Entails?(KB, s)
            2.     sym = list of proposition symbols in KB and s
            3.     return TT-Check-All(KB, s, sym, {})
            
            4.   Function TT-Check-All(KB, s, sym, model)
            5.     if Empty?(sym)
            6.       if PL-True?(KB, model) return PL-True?(s, model)
            7.       else return true
            8.     else
            9.       P = First(sym)
            10.      rest = Rest(sym)
            11.      return (TT-Check-All(KB, s, rest, model + {P = true}) and
                             TT-Check-All(KB, s, rest, model + {P = false}))
            
                 PL-True?(S, m) returns true if sentence-set S holds within 
                  model m and false otherwise.
            

            Note that this algorithm uses depth-first search to implicitly generate and explore the basic complete model-tree for KB and s to enumerate all models for which both KB and s are true.
          • EXAMPLE: The basic complete model-tree for the sentence ``not A or B" in propositional logic relative to variable-ordering B -> A and value-ordering F -> T.

            

            Note that all nodes in the tree corresponding to consistent models have ben circled.

          • This algorithm is sound (as it directly implements the definition of entailment) and complete (because it works for any KB and s, and always terminates as there are only finitely many models to examine).
          • Note that "finitely many" is not always the same as "few"; for our WW example in which s = not P12, the relevant symbols in KB and s are B11, B21, P11, P12, P21, P22, and P31, which have 2^7 = 128 possible models.
          • More generally, if there are n propositional symbols in KB and s, the algorithm above runs in O(2^n) time, which is true of every known inference algorithm for PL (and may be impossible to better for all inputs as propositional entailment is coNP-complete and probably no easier than NP-complete).
        • Advanced model checking
          • We will look at two families of algorithms that perform well in practice using model-tree pruning and local search, respectively.
          • We also i) rephrase entailment statements KB => s {which is equal to not KB or s) as determining the unsatisfiability of (KB and not s) (which is obtained from the above by applying DeMorgan's Law) and ii) rephrase both KB and s in Conjunctive Normal Form (CNF) in which a sentence is a conjunction (AND) of disjunctive (OR) clauses, e.g., (A or not B) and (B or not C or D) and (B or D).
            • There is a standard procedure for transforming an arbitrary PL sentence into a CNF equivalent (RN3, pp. 253-254).
            • As many other problems can be reduced to CNF SAT, our derived algorithms have a much broader applicability.
          • Backtracking + heuristics (Davis-Putnam-Logeman-Loveland (DPLL))
            • DPLL is a depth-first search of the model-tree that uses partial model unsatisfiability and various sentence-reducing heuristics to prune subtrees containing non-satisfying models, e.g.,
              • Pure heuristic: Assign pure symbols (symbols that have the same sign in all occurrences) the value that makes them true.
              • Unit heuristic: Assign symbols in single-symbol clauses the value that makes them true.
              Note that both heuristics when invoked may trigger a cascade of subsequent sentence reductions.
            • ALGORITHM: DPLL-Satisfiable? (RN3, Figure 7.17)

              1.   Function DPLL-Satisfiable?(s)
              2.     sym = list of proposition symbols in s
              3.     cls = list of clauses in CNF representation of s
              4.     return DPLL(cls, sym, {})
              
              5.   Function DPLL(cls, sym, model)
              6.     if every clause in cls is true in model return true
              7.     if some clause in cls is false in model return false
              8.     (P, value) = Find-Pure-Symbol(sym, cls, model)
              9.     if P is non-null return DPLL(cls, sym - P, model + {P = value})
              10.    (P, value) = Find-Unit-Clause(cls, model)
              11.    if P is non-null return DPLL(cls, sym - P, model + {P = value})
              12.    P = First(sym)
              13.    rest = Rest(sym)
              14.    return (DPLL(cls, rest, model + {P = true}) or
                             DPLL(cls, rest, model + {P = false}))
              

            • A variety of scale-up enhancements to the DPLL algorithm, e.g., variable and value ordering, allow modern SAT solvers to tackle input instances with tens of millions of variables.
          • Local search
            • Uses a model-evaluation function h(m) that counts the number of clauses in the given instance of CNF SAT that are not satisfied by m.
            • At each step, the algorithm picks an unsatisfied clauses and selects at random one of two ways to chose a variable in that clause to flip.
            • ALGORITHM: WalkSAT (RN3, Figure 7.18)

              1.   Function WalkSAT(cls, p, maxFlips)
              2.     model = random assignment of true / false to symbols in cls
              3.     for i = 1 to maxFlips do
              4.       if model satisfied all clauses in cls return model
              5.       c = randomly-selected clause in cls that is false in model
              6.       with probability p
              7.         flip the value in model of a randomly-selected 
                          symbol in cls
              8.       else
              9.         flip the value in model of whichever symbol in cls whose
                           flipped value maximizes the number of satisfied clauses 
              10.    return failure
              

            • A returned failure can mean either that we did not give the algorithm enough time or that the given sentence is unsatisfiable; only the former can be fixed by increasing maxFlips. Hence, WalkSAT is more commonly used when we expect that a solution exists then when we need to show unsatisfiability / entailment.

Wednesday, November 5

• In-class Exam #2 Notes
  I've finished making up the second in-class exam. The exam will be closed-book and written in-class on paper (please bring your own pens). It will be 75 minutes long and has a total of 50 marks (this is not coincidental; I have tried to make the number of marks for a question times 1 1/2 approximately equivalent to the number of minutes it should take you to do that question). The exam will cover material in course lectures #7-12. There will be three questions:
  1. Topics 3, 5, and 6 (4 parts / 14 marks total)
  2. Topics 4 and 6 (2 parts / 12 marks total)
  3. Topics 5 and 6 (3 parts / 24 marks total)

  I hope the above helps, and I wish you all the best of luck with this exam.

Thursday, November 6 (Lecture #12)
[RN3, Chapter 7; Class Notes]

• Logical reasoning (Cont'd)
  • Propositional logic (PL) (Cont'd)
    • PL Inference procedures (Cont'd)
      • Theorem proving
        • Given a knowledge base KB, a sentence s, and a set R of inference rules, each of which specifies a new sentence that is implied by one or more existing sentences, derive a sequence of applications of rules in R to KB that results in s, i.e., a proof that KB entails s.
          • If the number of models is large but the length of the proof is short, theorem proving can be more efficient then model checking.
        • Inference and proofs
          • An inference rule that says sentences s1, s2, ..., sn imply sentence s is written as

            s1 s2 ... sn
            ------------
                  s
            

          • Two classic inference rules:
            • Modus Ponens (Latin: "mode that affirms")

              s1 => s2   s1
              -------------
                    s2
              

            • AND-elimination

              s1 and s2
              ---------
                 s1
              

          • Other inference rules can be derived from logical equivalences.
            • Two sentences s1 and s2 are logically equivalent, i.e., s1 leq s2, if they are true for the same models.
            • Any logical equivalence s1 leq s2 has two associated inference rules

                s1      s2
              -----    ----
                s2      s1
              

              As such, each logical equivalence allows inference in two directions. Note that Modus Ponens and AND-elimination can only infer in one direction.
            • Standard logical equivalences (Table 7.11)

              

          • EXAMPLE: Theorem Proving by Hand in Wumpus World (Part I)
            • Recall the following simple KB for WW when we are trying to establish not P12 (there is no pit in [1,2]):
              • R1: not P11 (there is no pit in [1,1])
              • R2: B11 <=> (P12 or P21)
              • R3: B21 <=> (P11 or P22 or P31)
              • R4: not B11
              • R5: B12
            • We can prove not P12 as follows:
              1. Apply biconditional elimination to R2:
                 • R6: (B11 => (P12 or P21) and ((P12 or P21) => B11))
              2. Apply AND-elimination to R6:
                 • R7: (P12 or P21) => B11
              3. Apply contrapositive to R7:
                 • R8: not B11 => not (P12 or P21)
              4. Apply Modus Ponens to R8 and percept R4:
                 • R9: not (P12 or P21)
              5. Apply De Morgan's Rule to R9:
                 • R10: not P12 and not P21
              6. Apply AND-elimination to R10:
                 • R11: not P12
          • Observe that such logical inference is monotonic, i.e., the number of sentences in KB never decreases.
        • We can automate the theorem proving process using any of our search algorithms (informed or uninformed) relative to the following search problem:
          • Initial State: Knowledge base KB = KB0.
          • Actions: Inference rule-set R, with the proviso that the viable actions for any state KBi, i geq 0, is the set of rules whose top half matches KBi.
          • Result: The result of applying any viable action is to add the sentence in the lower half of that rule to KBi to create KB(i+1).
          • Goal: Wanted sentence s is in KBi, i geq 0.
          Courtesy of the monotonicity of logical inference, it is guaranteed that any order of application of valid inference rules in a proof will lead to the wanted sentence s if such a proof is possible wrt KB and R.
        • In many cases, proof search can be more efficient than model checking because it ignores irrelevant propositions, no matter how many of them there are, e.g., the WW proof above only requires R2 and R4, even if there were millions of sentences in KB in addition to R1, R3, and R5!
        • Wait a minute .. Before we get too excited, read the fine print, i.e., the phrase "if such a proof is possible wrt KB and R".
          • The above establishes that logical inference is sound -- how do we ensure that it is complete?
          • Using a complete search algorithm helps; however, we also need to ensure that our set R of inference rules is powerful enough. For example, if biconditional elimination was not part of R, the WW theorem proving example above would not work.
          • How do we determine if a given R is powerful enough to do what we want?
        • Proof by resolution
          • Ensures sound and complete logical inference with a single inference rule!!!
          • Let us first consider the unit resolution rule, which holds if li and m are complementary literals, i.e., one is the complement of the other:

                       l1 or l2 or ... or lk   m
            ------------------------------------------------
            l1 or l2 or ... or l(i-1) or l(i+1) or ... or lk
            

            Any sentences derived using the unit resolution rule are called resolvents.
          • EXAMPLE: Theorem Proving by Hand in Wumpus World (Part II)
            • Recall the following KB for WW after we established not P12 (there is no pit in [1,2]):
              • R1: not P11 (there is no pit in [1,1])
              • R2: B11 <=> (P12 or P21)
              • R3: B21 <=> (P11 or P22 or P31)
              • R4: not B11
              • R5: B12
              • R6: (B11 => (P12 or P21) and ((P12 or P21) => B11))
              • R7: B11 => (P12 or P21)
              • R8: not B11 => not (P12 or P21)
              • R9: not (P12 or P21)
              • R10: not P12 and not P21
              • R11: not P12
            • When the agent returned from [2,1] to [1,1] and then went to [1.2], recall that it perceived a stench but no breeze. We can now add the following facts to KB:
              • R12: not B12
              • R13: B12 <=> (P11 or P22 or P12)
            • Using a process similar to that by which we established R11 earlier, we can now derive the following:
              • R14: not P22
              • R15: not P13
            • We can also apply biconditional elimination R3, followed by Modus Ponens with R5:
              • R16: P11 or P22 or P31
            • Now, the question is, where is the pit? To find out, we first apply the unit resolution rule to R16 and R14:
              • R17: P11 or P31
            • Finally, we apply the unit resolution rule to R17 and R1:
              • R18: P31
              This establishes definitely that the pit is in [3,1].
          • Let us now extend the unit resolution rule to create the (generalized) resolution rule, which holds if li and mj are complementary literals:

                 l1 or ... or lk   m1 or ... or mn
            ---------------------------------------------
            l1 or ... or l(i-1) or l(i+1) or ... or lk or 
            m1 or ... or m(j-1) or m(j+1) or ... or mn
            

            This rule is sound (RN3, p. 253).
            • Note that this rule will actually eliminate all pairs of complementary literals in the union of l and m, e.g., the result of applying the the generalized resolution rule to l = (A or not B or C or not D) and m = (not A or B or C or D) is C.
          • Observe that if repeated applications of the resolution rule to a CNF sentence s results in the empty clause then s is unsatisfiable (as a disjunctive clause is true if and only if that clause has at least one literal that evaluates to true). Given that KB |= s if and only if (KB and not s) is unsatisfiable, we now have a resolution-based algorithm for proving entailment.
          • EXAMPLE: Theorem Proving by Hand in Wumpus World (Part III)
            • Suppose the agent in WW is in [1,1], perceives no breeze, and wishes to establish that there is no pit in [1,2], i.e., not P12. The relevant knowledge base is
              KB = R2 and R4 = (B11 <=> P12 or P21) and not B11

              which means that

              KB and not (not P12)= ((B11 <=> P12 or P21) and not B11 and P12)

              whose CNF form has five disjunctive clauses:

              • C1: not P21 or B11
              • C2: not B11 or P12 or P21
              • C3: not P12 or B11
              • C4: not B11
              • C5: P12

              Observe that the resolution of C3 and C4 gives clause (not P12), whose resolution with C5 is the empty clause. Hence, there is no pit in [1,2].

          • ALGORITHM: PL-Resolution (RN3, Figure 7.12)

            1.   Function PL-Resolution(KB, s)
            2.     cls = list of clauses in CNF representation of (KB and not s)
            3.     new = {}
            4.     while (true)
            5.       for each pair of clauses (ci, cj) in cls do
            6.         resolvents = PL-Resolve(ci, cj)
            7.         if resolvents contains the empty clause return true
            8.         new = new + resolvents
            9.       if new \subseteq cls return false
            10.      cls = cls + new
            
                  PL-Resolve(c1, c2) returns the set of all possible clauses
                   obtained by resolving c1 and c2.
            

            It can be shown that this algorithm is both sound (RN3, p. 253) and complete (RN3, pp. 255-256).
• NOTE: This lecture also included the introduction to inference over definite clause knowledge bases, which has been moved to the beginning of Lecture #13 for ease of reading.

Wednesday, November 12 (Lecture #13)
[RN3, Chapter 7; Class Notes]

• Logical reasoning (Cont'd)
  • Propositional logic (PL) (Cont'd)
    • PL Inference procedures (Cont'd)
      • Theorem proving (Cont'd)
        • There are a number of cases in which the full power of resolution is not needed to do logical inference. One restricted case that allows efficient (indeed, linear time) inference is knowledge bases composed of definite clauses.
          • A definite clause is a disjunction of one or more literals in which exactly one literal is positive, e.g., (not P or Q), (P or not Q or not R), and (R) are all definite clauses while (not P or not R) and (not Q) are not.
          • Knowledge bases containing only definite clauses are interesting for three reasons:
            1. Any definite clause can be rewritten as a conjunction of the negations of the negated literals (the clause's premise) that implies the unnegated literal (the clauses' conclusion), e.g., (P or not Q or not R) is logically equivalent to (Q and R) => P. A definite clause with one literal is logically equivalent to True and is called a fact.
            2. Logical inference over definite clauses can be done by either the forward or backward chaining algorithms.
            3. Both of these algorithms, when implemented carefully, run in time linear in the size of KB.
          • Both of these algorithms can perhaps best be explained by visualizing a definite clause KB as an AND-OR graph.
            • An AND-OR graph is a directed graph in which each non-leaf vertex is either an AND vertex or an OR vertex.
            • A definite clause KB can converted to an AND graph in which:
              1. each symbol is a vertex;
              2. each fact is a leaf;
              3. each symbol which is the conclusion of exactly one clause is an AND-vertex which is connected to the symbol-vertices in that clause's premise; and
              4. each symbol which is the conclusion of multiple clauses is an OR-vertex connected to the AND-vertices corresponding to these clauses, each of which is in turn connected to the symbol-vertices in their respective premises.
          • EXAMPLE: A definite clause KB and its associated AND-OR graph (RN3, Figure 7.16)

            

            In the examples below, the five clauses will be abbreviated as Q, P, M, L1, and L2, respectively.
        • Forward Chaining (FC)
          • Starting from facts in the KB, FC proves successively more implications using the clauses in KB until either a wanted query-symbol qs is proved true or no more clauses can be applied to derive new implications, i.e., qs is false.
          • ALGORITHM: PL-FC-Entails? (RN3, Figure 7.15) [ASSIGNMENT #3]

            1.   Function PL-FC-Entails?(KB, qs)
            2.     count = a table, where count[c] is the number of
                            symbols in clause c's premise
            3.     inferred = a table, where inferred[s] is initially 
                               false for each symbol s
            4.     agenda = a queue of symbols; initialized to all symbols 
                             known to be true in KB
            5.     while (agenda is not empty)
            6.       p = agenda.pop()
            7.       if (p = qs) return true
            8.       if (inferred[p] = false)
            9.         inferred[p] = true
            10.        for each clause c in KB where p is in c.premise do
            11.          count[c] = count[c] - 1
            12.          if (count[c] = 0)
            13.            agenda.push(c.conclusion)
            14.    return false
            

          • EXAMPLE: FC on a definite Clause KB
            • Suppose we want to prove that qs = Q is entailed by the definite clause KB in the example above.
            • Starting with facts A and B on the agenda queue and premise counts for L1, L2, M, P, and Q set to 2, 2, 2, 2, and 1, respectively the following happens in each while-loop iteration:
              1. Pop A; A inferred; premise counts for L1 and L2 each reduced by 1.
              2. Pop B; B inferred; premise counts for M and L2 each reduced by 1; as L2's premise count goes to 0, push L onto agenda.
              3. Pop L; L inferred; premise counts for P and M each reduced by 1; as M's premise count goes to 0, push M on agenda.
              4. Pop M; M inferred; premise count for P reduced by 1; as P's premise count goes to 0, push P onto agenda.
              5. Pop P; P inferred; premise counts for Q and L1 each reduced by 1; as both Q's and L1's premise counts go to 0, push Q and L onto agenda.
              6. Pop Q; as qs = Q, return True.
              Note in the above that clauses are processed in the order in which they are given.
          • FC is sound as every inference is an application of Modus Ponens. FC is also complete as every entailed atomic sentence will eventually be derived (RN3, p. 258).
          • FC is an example of data-driven reasoning. It can be used to derive implications from incoming percepts without a guiding query; if so, it must be kept under tight control lest KB be swamped with irrelevant conclusions ("There are a million things that are true. The question is, which ones are relevant?" -- Barbara Gowdy, "Lizards").
          • EXAMPLE: Consider the set of definite clauses in the second test-set of Assignment #3 (DCClause2.txt):

            Clauses   5
            1: A + B => S1
            2: A + C + D => S2
            3: C + D => S3
            4: S1 + S3 => D1
            5: S2 + S3 => D2
            					

            The implications derived by FC from each possible set of facts relative to these clauses is given in the following table:

            Available Facts	Derived Implications
            	S1	S2	S3	D1	D2
            {A}
            {B}
            {C}
            {D}
            {A,B}	X
            {A,C}
            {A,D}
            {B,C}
            {B,D}
            {C,D}			X
            {A,B,C}	X
            {A,B,D}	X
            {A,C,D}		X	X		X
            {B,C,D}			X
            {A,B,C,D}	X	X	X	X	X

          • FC as given here can state whether or not there is a proof linking available facts to a specified implication; however, it does not give any let alone all such proofs (which is required for explainability, e.g., medical diagnosis).

Thursday, November 13

• In-class Exam #2

Tuesday, November 18 (Lecture #14)
[RN3, Chapter 7; Class Notes]

• Went over In-class Exam #2.
• Logical reasoning (Cont'd)
  • Propositional logic (PL) (Cont'd)
    • PL Inference procedures (Cont'd)
      • Theorem proving (Cont'd)
        • Inference over definite clause databases (Cont'd)
          • Backward chaining (BC)
            • Starting from wanted query-symbol qs in the KB, BC runs successively more clauses in reverse until either all true facts required by the premises of these clauses are found (i.e., qs is true) or not (i.e., qs is false).
            • The path from qs to the current symbol being explored is maintained to keep the process from going into infinite loops associated with cycles in the AND-OR graph (RN3, p. 136).
            • ALGORITHM: PL-BC-Entails? (Adapted from RN3, Figure 4.11) [ASSIGNMENT #3]

              
              1.   Function PL-BC-Entails?(KB, qs)
              2.     inferred = a table, where inferred[s] is initially 
                                 true for each fact and false for each other
                                 symbol 
              3.     return ORSearch(KB, qs, inferred, [])
              
              4.   Function ORSearch(KB, s, inferred, path)
              5.     if (inferred[s] = true) return true
              6.     if (s is on path) return false
              7.     for (each clause c in KB such that s = c.conclusion)
              8.       if (ANDSearch(KB, c.premise, inferred, [s | path]) = true)
              9.           return true
              10.    return false
              
              11.    Function ANDSearch(KB, premise, inferred, path)
              12.      for (s in premise)
              13.        if (ORSearch(KB, s, inferred, path) = false)
              14.          return false
              15.        inferred[s] = true
              16.      return true
              

            • EXAMPLE: BC on a definite Clause KB
              • Suppose we want to prove that qs = Q is entailed by the definite clause KB in the example above.
              • Starting with the call PL-BC-Entails(KB, Q) the following happens:

                 1.  Call ORSearch(KB, Q, inferred, [])
                 2.    Call ANDSearch(KB, {P}, inferred, [Q])
                 3.      Call ORSearch(KB, P, inferred, [Q])
                 4.        Call ANDSearch(KB, {L,M}, inferred, [P Q])
                 5.          Call ORSearch(KB, L, inferred, [P Q])
                 6.            Call ANDSearch(KB, {A, P}, inferred, [L P Q])  # Processing L1
                 7.              Call ORSearch(KB, A, inferred, [L P Q])
                 8.              Return true; go back to (6).
                 9.              Call ORSearch(KB, P, inferred, [L P Q])
                10.              Return false; go back to (6).
                11.            Return false; go back to (5).
                12.            Call ANDSearch(KB, {A, B}, inferred, [L P Q])  # processing L2
                13.              Call ORSearch(KB, A, inferred, [L P Q])
                14.              Return true; go back to (12).
                15.              Call ORSearch(KB, B, inferred, [L P Q])
                16.              Return true; go back to (6).
                17.            Return true; go back to (5).
                18.          L is inferred; Return true; go back to (4).
                19.          Call ORSearch(KB, M, inferred, [P Q])
                20.            Call ANDSearch(KB, {B, L}, inferred, [M P Q])
                21.              Call ORSearch(KB, B, inferred, [M P Q])
                22.              Return true; go back to (20).
                23.              Call ORSearch(KB, L, inferred, [M P Q])
                23.              Return true; go back to (18).
                24.            Return true; go back to (5).
                24.          M inferred; Return true; go back to (4).
                25.        Return true; go back to (3).
                26.      P inferred; Return true; go back to (2).
                27.    Return true; go back to (1).
                28.  Return true.
                

                Note in the above that clauses are processed in the order in which they are given.
            • BC is sound and complete.
            • BC is an example of goal-driven reasoning; as BC only invokes relevant clauses and facts, its runtime behaviour is often for less than linear in the size of KB.
            • EXAMPLE: Consider the set of definite clauses in the second test-set of Assignment #3 (DCClause2.txt):

              Clauses   5
              1: A + B => S1
              2: A + C + D => S2
              3: C + D => S3
              4: S1 + S3 => D1
              5: S2 + S3 => D2
              					

              The facts required for BC to derive each possible implication relative to these clauses are given in the following table:

              Derivable implications	Required Facts
              	A	B	C	D
              S1	X	X
              S2	X		X	X
              S3			X	X
              D1	X	X	X	X
              D2	X		X	X

              Note that we are assuming here that each implication can only be derived in one way and hence has only one set of required facts. If an implication was derivable in several ways, we would have to list for each implication the fact-sets relative to which that implication would be derived. For example, if there was an additional clause "B + C => S1" in the above, S1 would be derivable via the fact-sets {A,B} and {B,C}.

            • BC as given here can state whether or not the available facts allow a proof of a specified implication; however, it does not give any let alone all such proofs (which is required for explainability, e.g., medical diagnosis).
        • INTERLUDE: A look at the mechanics of Assignment #3.

Thursday, November 20 (Lecture #15)
[RN3, Chapter 7; Class Notes]

• Logical reasoning (Cont'd)
  • Propositional logic (PL) (Cont'd)
    • Agents based on propositional logic
      • The first problem confronting a PL-based agent is deducing the current state of the world given initial knowledge and previous percepts and actions.
        • Recall that initial knowledge states facts that are always always true, e.g., there is always at least one wumpus (W11 or W12 or ... or W44) and and there is always at most one wumpus (not W11 or not W12, not W1 or not W13, ..., not W43 or not W44, i.e., at least one of each pair of locations is wumpus-free). The variables involved in such knowledge are called atemporal.
        • Subsequent knowledge wrt percepts and actions is time-specific, e.g., Stench^3, not Stench^4; the variables involved in such knowledge are fluents.
        • To handle fluents, we need a transition model that incorporates both translations of fluents to atemporal variables, e.g., L^t_xy => (Breeze^t <=> Bxy), and effect axioms that specify how actions in time changes variable values, e.g., L^0_11 and FacingEast^0 and Forward^0 => (L^1_21 and not L^1_11).
        • Note that to allow proper inference, we also have to explicitly specify what doesn't change over time, e.g., if we have an arrow at time 1 and move forward then we still have an arrow at time 2; the difficulties in establishing what needs to be thus specified and furthermore what needs to projected forward in time wrt k-step plans are known as the representational and inferential frame problems, respectively.
        • The former is often dealt with by invoking the spatial and temporal locality of typical actions and the latter by changing the focus from writing axioms about actions to axioms about fluent-change (successor-state axioms), e.g., HaveArrow^{t+1} <=> (HaveArrow^t and not Shoot^t).
      • We can combine logical inference and search to create a hybrid agent for a problem.
      • ALGORITHM: Hybrid agent for Wumpus World (RN3, Figure 7.20)

        1.   Function Hybrid-Wumpus-Agent(KB, percept, t, plan)
        2.     TELL(KB, makePerceptSEntence(percept, t))
        3.     Tell the KB the temporal "physics" sentences for time t
        4.     safe = {[x,y] | ASK(KB, OK^t_(x,y} = true}
        5.     if (ASK(KB, Glitter^t) = true)
        6.       plan = [Grab] + planRoute(current,{[1,1]}, safe) + [Climb]
        7.     if (plan is empty)
        8.       unvisited = {[x,y] | ASK(KB, L^t'_(x,y) = false for all t' <= t}
        9.       plan = planRoute(current, univisited \intersect safe, safe)
        10.    if (plan is empty and ASK(KB, HaveArrow^t) = true)
        11.      posssibleWumpus = {[x,y] | ASK(KB, not W_(x,y) = false}
        12.      plan = planShot(current, possibleWumpus, safe)
        13.    if (plan is empty)  \\ No choice but to take a risk
        14.      notUnsafe = {[x,y] | ASK(KB, not OK^t_(x,y) = false}
        15.      plan = planRoute(current, univisited \intersect notUnsafe, safe)
        16.    if (plan is empty)
        17.      plan = planRoute(current, {[1.1]},safe) + [Climb]
        18.    action = plan.pop()
        19.    TELL(KB, makeActionSEetence(action, t)
        20.    t = t + 1
        21.    return action
        
        22.    Function planRoute(current, goals, allowed)
        23.      problem = routeProblem(current, goals, allowed)
        24       returnA*GraphSearch(problem)
        
             Initial call: Hybrid-Wumpus-Agent(KB, percept, 0, {})
        

        Note that this agent constructs plans based on a fixed decreasing priority of goals (grab gold if present and then leave cave => visit somewhere new that is totally safe => shoot arrow at possible wumpus => visit somewhere new that may not be totally safe => leave cave without gold but nonetheless alive).
      • We can also have an agent that constructs plans using only logical inference. This is done in three steps:
        1. Constuct a sentence that includes:
           1. Init^0 (a collection of assertions about the initial state);
           2. Transition^1, Transition^2, ..., Transition^t (the successor-state axioms for all actions at all times up to a maximum time t); and
           3. The assertion that the goal is achieved at time t, e.g., HaveGold^t and ClimbedOut^t.
        2. Present the whole sentence to a SAT solver. If the solver finds a satisfying model, the goal is achievable; else, the planning problem is impossible.
        3. If a satisfying model was found in (2), extract the plan consisting of those action-variables that were assigned the value True.
      • ALGORITHM: SATPlan (RN3, Figure 7.22)

        1.   Function SATPlan(problem = (init, transition, goal), Tmax)
        2.     for t = 0 to Tmax do
        3.       cnf = TranslateToCNF(problem, t)
        4.       model = SATSolver(cnf)
        5.       if (model is not null)
        6.         return ExtractSolution(model)
        7.     return failure
        

      • As satisfaction is not entailment, SATPlan can find models with impossible or simultaneously-executed actions if the specifying sentence is incomplete, e.g., lacks precondition and/or action exclusion axioms; hence, even if hybrid agents are ultimately used, SATPLan is typically employed during knowledge-base development as a debugging tool.
    • Knowledge-bases created with propositional logic can be ludicrously large; for smaller KB, we need to consider representation languages that have more expressive power.
    • Languages differ in what they assume about what exist in the world (ontological commitments) and what an agent believes about facts (epistemological commitments), e.g., Figure 3.1 in RN3:

      Language	Ontological	Epistemological
      Propositional logic	facts	true/false/unknown
      First-order logic	facts, objects, relations	true/false/unknown
      Temporal logic	facts, objects, relations, times	true/false/unknown
      Probability theory	facts with degree of belief (in [0,1])	true/false/unknown
      Fuzzy logic	facts with degree of truth (in [0,1])	known interval value

      Focus here on first-order logic.

    • First-order logic (FOL)
      • Also known as first-order predicate calculus
      • First-order logic is an intermediate language that combines the rigor of propositional logic and the expressive power of natural language.
        • At the core of this expressivity are objects, relations, and functions, e.g.,
          • Objects: Wumpus, Ronald McDonald, baseball games, centuries.
          • Relations: Unary (properties) (red, round, prime), n-ary (brother, bigger than, comes between).
          • Functions: father of, one more than, beginning of.
        • FOL can encode almost any assertion with these, e.g.,
          • "one plus two equals three"
          • "squares neighbouring the wumpus are smelly"
          • "King John ruled England in 1200"
        • FOL is also to express that assertions hold relative to all or only some objects, e.g.,
          • "every dog bites"
          • "some cats are black"
          • "there is someone for everybody"
          Note that such qualification may (as in the third example) be nested.
      • Syntax and semantics
        • The syntax of first-order logic builds on and extends that given previously for propositional logic.
          • Where symbols in PL were Boolean variables, symbols in FOL can be variables of any type, functions, predicates or constants.
          • Atomic and complex sentences are also broadened in FOL to allow recursively-embedded predicates and functions as well as nested Exists and ForAll quantifiers.
        • Syntax of first-order-logic (RN3, Figure 8.3)

          

        • EXAMPLE: Objects, predicates and functions:
          • Objects: John, Richard, Crown
          • Predicates: isKing(), isGold(), areMarried()
          • Functions: LeftLeg(), Father(), Mother()
          The arity of a predicate or function is the number of parameters of that predicate or function, e.g., the arities of isKing(), areMarried(), and Father() are 1, 2, and 1, respectively.
        • EXAMPLE: Atomic and complex sentences
          • Atomic: Brother(Richard, John), areMarried(Father(Richard), Mother(John))
          • Complex: not Brother(LeftLeg(John), Richard), isBrother(John, Richard) and isBrother(Richard, john), not isKing(John) => isKing(Richard)
        • EXAMPLE: Quantified sentences
          • ForAll: ForAll x (isKing(x) => isPerson(x))
          • Exists: Exists x (isKing(x))
          • Nested: ForAll x (Exists y, t (isPerson(x) and isPerson(y) and isTime(t) => Loves(x, y, t)))
        • The semantics of POL, like PL, is based on models. Models in FOL are more complex, as each such model consists of a set of objects and an interpretation that maps constant symbols to objects, predicate symbols to relations on these objects, and function symbols to functions on these objects.
          • As the number of objects may be infinite, e.g., the positive integers, the number of possible models may be unbounded. Even if the number of objects is bounded, the possibilities in interpretation may still yield ludicrously large numbers of models, e.g., ~137 billion models for 6 objects under the interpretations allowed in Figure 8.4 of RN3.
          • For these reasons, model checking by complete enumeration of all possible models is not feasible in many cases or possible in others.
      • EXAMPLE: The basic biological kinship domain.
        • Is based on the domain of objects that are persons, the unary predicates isMale() and isFemale(), the binary predicates isParent(), isSibling(), isBrother(), isSister(), isChild(), isSon(), isDaughter(), isSpouse(), isHusband(), isWife(), isGrandParent(), isGrandChild(), isCousin(), isAunt(), and isUncle(), and the binary functions Mother() and Father().
        • We can on build on top of these basic objects, predicates, and functions to define various axioms, e.g.,
          • ForAll m, c (Mother(c) = m <=> isFemale(m) and isParent(m, c))
          • ForAll x (isMale(x) <=> not isFemale(x))
          • ForAll p, c (isParent(p, c) <=> isChild(c, p))
          • ForAll x, y, c (areParents(x, y, c) <=> x \neq y and isParent(x, c) and isParent(y, c))
          • ForAll x, y (isSibling(x, y) <=> x \neq y and Exists p (isParent(p, x) and isParent(p, y)))
        • We can also derive theorems from the given axioms, e.g., ForAll x, y (isSibling(x, y) <=> isSibling(y, x)) is implied by the isSibling() axiom above. To save on the computational cost of re-proving, we may choose to include basic theorems in a knowledge base.
        • Note that the above applies to basic biological kinship only and does not necessarily reflect other types of kinship, e.g., kinship in matrilineal or polygamous societies, kinship in families based on divorced, unmarried, or non-heterosexual partners => one must be exceptionally careful when constructing knowledge bases for real-world domains.
      • With the exception of those based on complete model enumeration, all of the PL inference algorithms seen previously have FOL analogues (see RN3, Chapter 9).
        • Efficient algorithms for forward and backward chaining in FOL (RN3, Sections 9.3 and 9.4) are the foundations of both logic programming languages like Prolog and (when combined with appropriate techniques for handling uncertainty (RN3, Chapter 14)) expert systems for real-world inference in domains such as medical diagnosis and finance.
      • Knowledge engineering with FOL
        • Knowledge engineering is the process by which we create and maintain knowledge bases for particular applications. We saw some very basic examples of this in our lectures on propositional logic and Assignment #3.
        • FOL allows the creation of far more powerful and versatile KBs. We consider here the process of creating special-purpose KB for carefully circumscribed domains whose full range of queries is known in advance, e.g., an online airline and hotel reservation system (techniques for engineering general-purpose KB for domains such as free-range natural language understanding are discussed in Chapter 12 of RN3).
        • The special-purpose KB creation process is as follows:
          1. Identify the task.
          2. Assemble relevant knowledge.
          3. Decide on a vocabulary of predicates, functions, and constants.
          4. Encode general knowledge about the domain.
          5. Encode a description of the specific problem instance.
          6. Pose queries to the inference procedure and get answers.
          7. Debug the knowledge base.

          This process is seldom a linear progression and it is often necessary to loop backwards to fix found problems; as such, the ideal KE process described above is very much like the waterfall model in software engineering.

        • Whether special- or general-purpose, knowledge engineering is never easy and must be done very, very carefully to ensure the consistency and completeness of derived KB wrt the given real-world application ("In much wisdom there is much grief, and he who increases knowledge increases sorrow." -- Andrei Rublev (1966))
    • FOL is very powerful but does not handle situations involving uncertainty, e.g., medical diagnosis; for this, we need to invoke special techniques, e.g., probabilistic reasoning (RN3, Chapters 13 and 14).
• Potential exam questions

References

• Adolfi, F., Vilas, M., and Wareham, T. (2024a) "Complexity-Theoretic Limits on the Promises of Artificial Neural Network Reverse-Engineering." In the Proceedings of the 46th Annual Meeting of the Cognitive Science Society (CogSci 2024).
• Adolfi, F., Vilas, M., and Wareham, T. (2024b) "The Computational Complexity of Circuit Discovery for Inner Interpretability." arXiv.2410.08025 (71 pages). [PDF]
• Adolfi, F., Vilas, M., and Wareham, T. (2025) "The Computational Complexity of Circuit Discovery for Inner Interpretability." In the Proceedings of the 13th International Conference on Learning Representations (ICLR 2025). Selected for Spotlight presentation because the contribution has been judged to be especially notable.
• Barcelo, P., Monet, M., Perez, J., and Subercaseaux, B. (2020) "Model interpretability through the lens of computational complexity." In Advances in neural information processing systems, 33, 15487-15498. [PDF]
• Bassan, S., Amir, G., and Katz, G. (2024) "Local vs. Global Interpretability: A Computational Complexity Perspective." arXiv preprint arXiv:2406.02981. [PDF]
• Bellogin, A., Grau, O., Larsson, S., Schimpf, G., Sengupta, B., and Solmaz, G. (2024) "The EU AI Act and the Wager on Trustworthy AI." Communications of the ACM, 67(12), 58-65. [PDF]
• Buyl, M. and De Bie, T. (2024) "Inherent Limitations of AI Fairness." Communications of the ACM, 67(2), 48-55. [HTML]
• Bylander, T. (1994) "The Computational Complexity of Propositional STRIPS Planning.: Artificial Intelligence, 69(1-2), 165-204.
• Cormen, T.H., Leiserson, C.E., Rivest, R.L., Stein, C. (2009) Introduction to Algorithms. Third Edition. The MIT Press; Cambridge, MA. [Abbreviated above as CLRS]
• Cusumano, M.A. (2025) "DeepSeek Inside: Origins, Technology, and Impact." Communications of the ACM, 68(7), 18-22. (PDF)
• Denning, P. (2025) "Three AI Futures." Communications of the ACM 69(9), 31-33. (PDF)
• Dhar, V. (2024) "The Paradigm Shifts in Artificial Intelligence." Communications of the ACM, 67(11), 50-59. [HTML]
• Fikes, R.E. and Nilsson, N.J. (1971) "STRIPS: A New Approach to the Application of Theorem Proving to Problem Solving." Artificial Intelligence, 2(3-4), 189-208.
• Garey, M.R. and Johnson, D.S. (1979) Computers and Intractability: A Guide to the Theory of NP-Completeness. W.H. Freeman; San Francisco, CA.
• Guest, O. and Martin, A. E. (2023) "On logical inference over brains, behaviour, and artificial neural networks." Computational Brain & Behavior, 6(2), 213-227 [PDF]
• Guest, O. and Martin, A.E. (2024) "A Metatheory of Classical and Modern Connectionism." Preprint. [PDF]
• Guest, O., Suarez, M., Muller, B.C.N., van Meerkerk, E., Beverborg, A.O.G., de Haan, R., Elizondo, A.R., Blokpoel, M., Scharfenberg, N., Kleinherenbrink, A., Camerino, I., Woensdregt, M., Monett, D., Brown, J., Avraamidou, L., Alenda-Demoutiez, J., Hermans, F., and van Rooij, I. (2025) "Against the Uncritical Adoption of 'AI' Technologies in Academia." Preprint. (PDF)
• Haigh, T. (2023a) "Conjoined Twins: Artificial Intelligence and the Invention of Computer Science." Communications of the ACM, 66(6), 33-37. [HTML]
• Haigh, T. (2023b) "There was No 'First' AI Winter." Communications of the ACM, 66(12), 35-39. [HTML]
• Haigh, T. (2024a) "How the AI Boom Went Bust." Communications of the ACM, 67(2), 22-26. [HTML]
• Haigh, T. (2024b) "Between the Booms: AI in Winter." Communications of the ACM, 67(11), 19-23. [HTML]
• Haigh, T. (2025) "Artificial Intelligence: Then and Now." Communications of the ACM, 68(2), 24-29. [HTML]
• Huxley, J. (1957) New Bottles for New Wine. Chatto & Windus.
• Kedia, A, and Rasu, M. (2020) Hands-On Python Natural Language Processing. Packt Publishing; Birmingham, UK.
• Livni, R., Shalev-Shwartz, S., and Shamir, O. (2014) "On the computational efficiency of training neural networks." Advances in Neural Information Processing Systems, 27, 1-9.
• Marcus, G. and Davis, E. (2019) Rebooting AI: Building Artificial Intelligence We Can Trust. Pantheon Books; New York.
• Marcus, G. and Davis, E. (2021) "Insights for AI from the Human Mind", Communications of the ACM, 64(1), 38-41. [Text]
• Newell, A. and Simon, H.A. (1956) The Logic Theory Machine: A Complex Information Processing System. RAND Technical Report P-868.
• Newell, A., Shaw, J.C., and Simon, H.A. (1959) Report on a General Problem Solving Program. RAND Technical Report P-1584.
• Newell, A. and Simon, H.A. (1972) Human Problem Solving. Prentice-Hall.
• Russell, S. and Norvig (2010) Artificial Intelligence: A Modern Approach (3rd Edition). Prentice-Hall.
• Russell, S. and Norvig (2022) Artificial Intelligence: A Modern Approach (4rd Edition). Prentice-Hall.
• Schmidhuber, J. (2015) "Deep learning in neural networks: An overview." Neural Networks, 61, 85-117.
• Schneier, B. (2025) "AI and Trust." Communications of the ACM, 68(8), 29-33. (PDF)
• Seuss, Dr. (1970) One fish two fish red fish blue fish. Random House.
• Shein, E. (2024) "The Impact of AI on Computer Science Education." Communications of the ACM, 67(11), 13-15. [HTML]
• Skinner, B.F. (1948) Walden Two. Hackett Publishing Company.
• Song, L., Vempala, S., Wilmes, J., and Xie, B. (2017) "On the complexity of learning neural networks." In Advances in Neural Information Processing Systems, 30, 1-9.
• Sutton, R.S. and Barto, A.G. (2018) Reinforcement Learning: An Introduction (Second Edition). The MIT Press. [Website]
• Van Rooij, I., Guest, O., Adolfi, F., de Haan, R., Kolokolova, A., and Rich, P. (2024) "Reclaiming AI as a theoretical tool for cognitive science." Computational Brain & Behavior, 1-21. [PDF]
• Wareham, T. (2022) "Creating Teams of Simple Agents for Specified Tasks: A Computational Complexity Perspective." CoRR abs/2205.02061 (20 pages). [PDF]
• Wareham, T. and Vardy, A. (2018) "Putting It Together: The Computational Complexity of Designing Robot Controllers and Environments for Distributed Construction." Swarm Intelligence, 12(2), 111-128.

Created: July 11, 2025
Last Modified: November 13, 2025