Materials:
Please bring scratch paper and pens/pencils.
During the quiz, you can use only the paper notes you made solving the lab, as well as the text of the lab itself.
Review:
Vocabulary
- Canonical CNF, canonical DNF, Boolean functions
- Sets, $\emptyset, \mathbb{N, Z, Q, R}$.
- Predicates, domain (universe) of a predicate, existential and universal quantifiers, predicate logic
- Free and bound variables, scope of quantifiers, prenex form.
Individual work
Solve each of the following exercises.
- For each of the following Boolean functions, construct a canonical CNF and a canonical DNF. Hint: you can write the whole truth table, but you don't necessarily need to.
- $AllTheSame(x,y,z)$ which returns true when either all its inputs are true, or all its inputs are false.
- $Parity(x,y,z)$ which returns true when an odd number of its inputs are true (that is, either one or three)
- Let $x = y, x < y, Even(x)$ and $Prime(x)$ be predicates. Translate the following from English to logic (you can use standard arithmetic operations). Make sure to specify domains of quantifiers using $\mathbb{N, Z, Q, R}$, and note which of these statements are true, and which are false.
- Every integer greater than n is not prime.
- There is a smallest natural number.
- If an integer gives the same value when multiplied by two different integers, that integer must be 0. (Hint: in order to ensure that two variables take different values state explicitly that they are not equal.)
- Which of the following pairs consist of equivalent formulas? That is, when is $F \equiv G$ for formulas below?
- $F=\forall x \forall y P(x,y)$, $G= \forall y \forall x P(x,y)$
- $F = \forall x \exists y P(x,y)$, $G = \forall y \exists x P(x,y)$
- $F=\forall x \forall y P(y,x)$, $G= \forall x \forall y P(x,y)$
- $F = \forall x \exists y P(x,y)$, $G = \exists x \forall y P(x,y)$
- Recall that a formula is in prenex form when each quantified variable has a unique name, and all quantifiers are in front of the formula. Now, convert each of the following into prenex form. For simplicity, start by opening up implications using $F \to G \equiv \neg F \vee G$ rule.
- $\forall x (\exists y P(x,y)) \to (\exists y Q(x,y))$
- $ (( \exists x P(x)) \to (\exists x \neg P(x))) \to (\exists x \forall y P(x) \vee \neg P(y)) $
- For each of the following formulas, negate them and simplify until all negations are on predicates. Use DeMorgan, double negation, definitions of implication and quantifiers.
- $\forall x \forall y \exists z, P(x,z) \wedge P(y,z) \to Q(x,y)$
- $\exists x \forall y Q(y,z) \wedge ((\forall z P(x,y,z)) \to Q(x,y))$
Group exercises
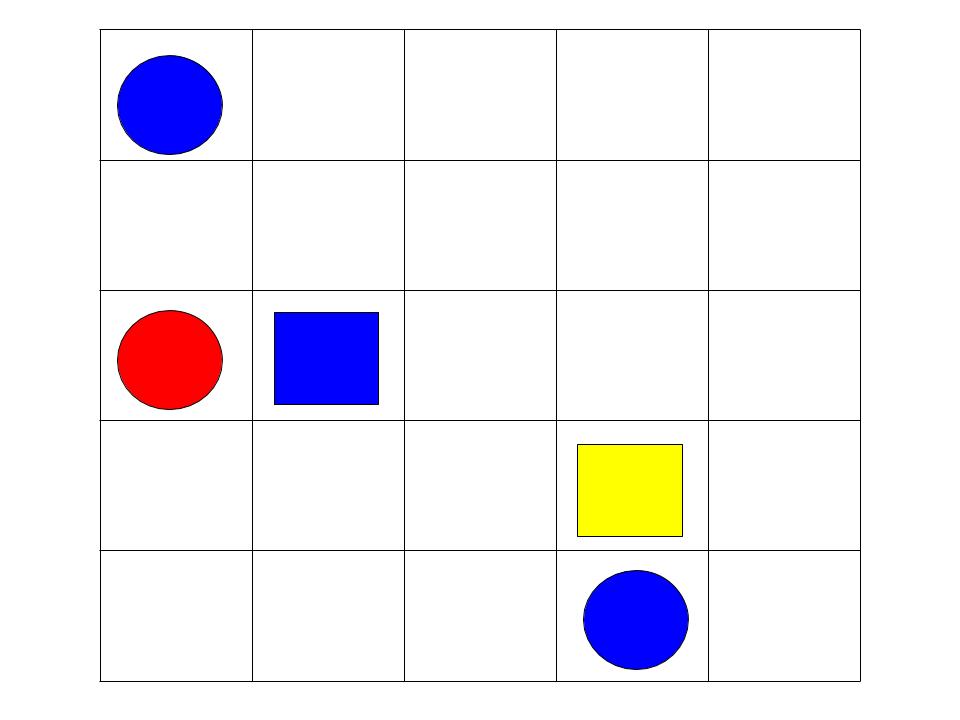 For this part of the lab, you will be exploring quantified statements in our version of Tarski World, again in groups of three. There, you have a board with pieces of different shapes and colours; these pieces form the universe of Tarski world. For each shape and each colour of a piece, you have a predicate, as well as a few predicates descibing a relation between pieces. In our lab, we will have predicates $Square(x)$, $Circle(x)$, $Red(x), Orange(x), Yellow(x), Green(x), Blue(x),$ as well as $NextTo(x,y)$, which is true iff $y$ is in a cell adjacent to $x$ (left/right/front/back of $x$), and $Aligned(x,y)$, which is true if $x$ and $y$ are either in the same column or in the same row. (Of course, you can use these predicates with any variable names, not just $x$ or $y$).
For this part of the lab, you will be exploring quantified statements in our version of Tarski World, again in groups of three. There, you have a board with pieces of different shapes and colours; these pieces form the universe of Tarski world. For each shape and each colour of a piece, you have a predicate, as well as a few predicates descibing a relation between pieces. In our lab, we will have predicates $Square(x)$, $Circle(x)$, $Red(x), Orange(x), Yellow(x), Green(x), Blue(x),$ as well as $NextTo(x,y)$, which is true iff $y$ is in a cell adjacent to $x$ (left/right/front/back of $x$), and $Aligned(x,y)$, which is true if $x$ and $y$ are either in the same column or in the same row. (Of course, you can use these predicates with any variable names, not just $x$ or $y$).
Now, you can write formulas such as $\exists x Blue(x)$ or $\forall x Square(x) \to \exists y Circle(y) \wedge NextTo(x,y)$, which says that every square has a circle next to it; note that the board on the picture satisfies both these formulas. For conciseness, we will often use just the first letter of the predicate (so the formulas above would be $\exists x B(x)$ and $\forall x (S(x) \to \exists y C(y) \wedge N(x,y))$
For the following exercises, each of you can make one board in exercise 1, write a formula for another's board in exercise 2, and a formula for third person's board in exercise 3; just make sure you all have different boards and formulas. Work together on all of these exercises.
Exercise 1:
Make three more boards satisfying $\forall x S(x) \to \exists y C(y) \wedge N(x,y)$ ). Try to use different numbers of pieces, and place them differently on the board.
Exercise 2:
For each of these boards, write a formula which is true for that board, but not for the original board. Use quantifiers in all of your formulas.
Exercise 3:
Now, for each of your three boards, write a formula which is false for that board, but would become true if you add, remove or move one piece. State which piece needs to be added/removed/moved and where.
Review after the group exercises
Consider a formula $\exists x Blue(x) \wedge ((\forall y Green(y) \to Aligned(x,y)) \vee (\exists z Square(z) \wedge NextTo(x,z))$
- Make a board where this formula is true.
- Make a second board where this formula is false, but changing one piece makes it true.
- For your second board, write a formula which is true for that board.
 For this part of the lab, you will be exploring quantified statements in our version of Tarski World, again in groups of three. There, you have a board with pieces of different shapes and colours; these pieces form the universe of Tarski world. For each shape and each colour of a piece, you have a predicate, as well as a few predicates descibing a relation between pieces. In our lab, we will have predicates $Square(x)$, $Circle(x)$, $Red(x), Orange(x), Yellow(x), Green(x), Blue(x),$ as well as $NextTo(x,y)$, which is true iff $y$ is in a cell adjacent to $x$ (left/right/front/back of $x$), and $Aligned(x,y)$, which is true if $x$ and $y$ are either in the same column or in the same row. (Of course, you can use these predicates with any variable names, not just $x$ or $y$).
For this part of the lab, you will be exploring quantified statements in our version of Tarski World, again in groups of three. There, you have a board with pieces of different shapes and colours; these pieces form the universe of Tarski world. For each shape and each colour of a piece, you have a predicate, as well as a few predicates descibing a relation between pieces. In our lab, we will have predicates $Square(x)$, $Circle(x)$, $Red(x), Orange(x), Yellow(x), Green(x), Blue(x),$ as well as $NextTo(x,y)$, which is true iff $y$ is in a cell adjacent to $x$ (left/right/front/back of $x$), and $Aligned(x,y)$, which is true if $x$ and $y$ are either in the same column or in the same row. (Of course, you can use these predicates with any variable names, not just $x$ or $y$).