MUN Computer Science 1002 - Lab 4

Predicates and quantifiers

Review:

Lectures 12-14.

Vocabulary

Universal modus ponens, rules of inference in predicate logic, universal/existential instantiation/generalization
Proofs, constructive proofs, counterexamples
Vacuously true

Individual work

Solve each of the following exercises.

Which of the following statements is true, and which is false? Here, $\emptyset$ denotes an empty set.
1. $\forall x \in \emptyset, x >x^2$
2. $\forall x, y \in \emptyset, P(x) \to P(y)$
3. $\exists x \in \emptyset, x^2 > x$
In the following arguments, fill in the blanks to make them valid. Note when the universal instantiation step happens.
Every day in February is cold
Valentine's day is in February
-----------------------------------------------------------------------
$\therefore$ ___________________________

For every real number x, if $x \neq 0$ then either $x <0$ or $x >0$.
For every real number x, if x > 0 then $x^2 > 0$
For every real number x, if x < 0 then $x^2 >0$
___________________________
-----------------------------------------------------------------------
$\therefore$ $k^2 > 0$
Give a counterexample to each of the following statements. If neither domain nor interpretations of predicates are given, then give all of those; if both are given, find an element in the domain which is a counterexample, and if only the domain is given, provide interpretations of predicates. (See slide 7 in lecture 12 for an example where you pick both the domain and the interpretation of predicates).
1. $( \exists x P(x)) \to (\forall x P(x))$
2. $ \forall x \in \mathbb{R}, x^2 \geq x$
3. $ \exists x \forall y \in \{0,1\}, P(x) \wedge P(y) \to x = y$
Now, for each of the three formulas in the previous question, give an example of a domain where it is true for any interpretation of predicates (in the last two formulas, change the domain from the given to yours).
Give a constructive proof of each of the following:
1. $\exists x \in \mathbb{Z}, x^2 = x$.
2. $\exists x, y, z \in \{0, 1\}, x = y \wedge x \neq z$.

Group activity

In this exercise, you will do a direct proof "by picture" of the famous Pythagoras's theorem. Work in groups of three; you can split roles as "geometer" (doing the work with the paper), "algebraist" (writing down the proof symbolically), and a "logician" (noting what rules of inference and axioms were used in each step of the proof). Please do not try to read the proof online, it is likely to be more confusing than to figure it out yourself given the steps -- besides, there is a large number of different proofs.

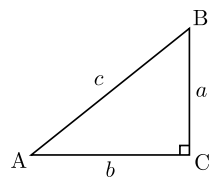trangle The statement of the Pythagoras' theorem is as follows: for every triangle with a right angle, the square of the side opposite to the right angle (hypotenuse) is equal to the sum of squares of the other two sides. That is, for every triple of numbers $a,b,c$ labelling sides of a right-angle triangle (right triangle) as in this picture (with c being a hypotenuse), $c^2 = a^2+b^2$.

Proof of Pythagoras' theorem
1. Take two pieces of paper (of arbitrary size, but same for both pieces, preferably squared).
2. Fold/cut them to make them into squares.
3. Pick an arbitrary point on the side of the square. Call the distance from this point to one end of that side "a", and to the other end of that side "b". Now, add lines to your two pieces of paper to make the following pictures (making sure your choice of a and b is the same everywhere):
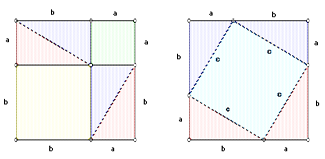
4. Looking at these two squares can already suggest to you a proof of the Pythagoras' theorem. To make it more formal, write three expressions for the area of the whole square: 1) by using just the lengths of its sides 2) by summing up areas of pieces in first square 3) by summing up the areas of the pieces in the second square. All you need here is that an area of a rectangle is a product of lengths of its sides.
5. Now, looking at the two squares, match up the pieces so that you are left with a square with side a and a square with side b on the first piece of paper, and a square with a side of c on the second. Take two corresponding expressions from the previous subquestion, equate them, and cancel out the pieces you have matched.
6. You should end up with a formula for Pythagoras' theorem.
7. Now, examine the assumptions (if any) you have made in the process. Explain why your proof generalizes to any right triangle. Would it generalize for a triangle which does not have a right angle?
8. Done!
A Pythagorean triple is any sequence of three natural numbers $a,b,c$ that satisfies the equation $a^2+b^2=c^2$.

Give an example of a Pythagorean triple
Based on what you learned from doing the proof of Pythagoras' theorem, can you show that there are infinitely many Pythagorean triples? (Hint: there are several ways of solving this problem. Try it, and then see if your group members came up with something different).

Review after the group activity

Consider the proof of Pythagoras' theorem.