Lab 1 COMP 1002

Language of propositional logic

Review:

• Unit 1 lectures and slides.
• Online exercises

Vocabulary

• Proposition, propositional variable, propositional formula,
• Logic connectives: AND ($\wedge$, conjunction), OR ($\vee$, disjunction), NOT ($\neg$, negation), IF .. THEN ($\to$, implication), IFF (biconditional, if and only if) $\leftrightarrow$
• Contrapositive, converse, inverse.
• Truth assignment, satisfying assignment, falsifying assignment, tautology, contradiction.
• Truth table, de Morgan's laws, double negation.
• Equivalence of formulas. Negation. Simplification. Definition of $\to$ in terms of $\neg, \vee$.

Materials

• Scratch paper, pens/pencils and erasers.

Warm-up exercises

Solve each of the following exercises.

1. Determine whether the each of the following sentences is true or false.
   1. Toronto is the capital of Canada.
      Answer

      False.

   2. Pianos or violins are string instruments (hint: pianos aren't, violins are).
      Answer

      True.

   3. If cows fly, then seagulls eat fish.
   Answer

   True. (Since cows don't fly, every formula of the form "if cows fly then ..." is (vacuously) true).

2. Let k be some specific number. Let A = "k is even", B = "k > 7", C = "k is prime".
   1. Write the following sentences about k as logical formulas using A, B, C:
      1. Number k is either even or greater than 7.
         Answer

         $A \vee B$

      2. If k is both even and prime, then in particular it is even.
         Answer

         $A \wedge C \to A$

      3. Either k is even, or k is prime, and not both.
         Answer

         $(A \vee C)\wedge \neg (A \wedge C)$

   2. Now, for the same A, B, C as above, write the following formulas in English.
      1. $ C \wedge B \to \neg A$
      Answer

      If k is prime and greater than 7, then k is not even

      2. $ \neg C \wedge A \wedge C$
      Answer

      k is not prime and k is even and k is prime.

      3. $ (A \wedge B) \to (A \wedge B)$
      Answer

      If k is prime and greater than 7, then k is prime and greater than 7.

   3. For each of the six formulas above, say if it is a tautology, a contradiction, or neither.
      Answer

      a(ii) and b(iii) are tautologies, b(ii) is a contradiction, the rest are neither.

   4. For each of the six formulas above which are neither tautology nor contradiction, give one satisfying assignment and one falsifying assignment to variables A, B, C.
      Answer

      a(i): A=false, B=false is a falsifying assignment. The rest (eg A=true, B=false) are satisfying.
      a(iii): A=false, B=false, and A=true, B=true are falsifying assignments. The rest (A=true, B=false, as well as A=false, B=true) are satisfying.
      b(i): A=true, B=true, C=true is a falsifying assignment, all the rest are satisfying assignments.

3. Let A = "There is a blizzard", B = "MUN is closed".
   1. Make English sentences using the propositions above which are equivalent to $A \to B$, using the following English sentence structures. For example, to express $A \to B$ using sentence structure " ... unless ...", you would have to say "MUN is closed unless there is no blizzard", and using sentence structure "... is sufficient for ...", you would say "A blizzard is sufficient for MUN to be closed".
      1. ... implies ...
      Answer

      There is a blizzard implies that MUN is closed

      2. ... if ...
      Answer

      MUN is closed if there is a blizzard

      3. ... only if ...
      Answer

      There is a blizzard only if MUN is closed

      4. ... whenever ...
      Answer

      MUN is closed whenever there is a blizzard

   2. Now, for the same A and B as above, write in English the sentence corresponding to $\neg B \to \neg A$. Then write converse of $\neg B \to \neg A$, inverse of $\neg B \to \neg A$, contrapositive of $\neg B \to \neg A$ and negation of $\neg B \to \neg A$, all simplified to remove double negations
      Answer

      Original sentence $\neg B \to \neg A$: If MUN is not closed then there is no blizzard.
      Converse: If there is no blizzard, then MUN is not closed.
      Inverse (simplified): If MUN is closed, then there is a blizzard
      Contrapositive (simplified): If there is a blizzard, then MUN is closed.
      Negation (simplified): MUN is not closed and there is blizzard.

   3. Now, group together the sentences you wrote above that are equivalent to each other.
      Answer

      "If there is a blizzard then MUN is closed" is equivalent to "If MUN is not closed then there is no blizzard".
      They are not equivalent to "If MUN is closed then there is a blizzard", which is equivalent to "If there is no blizzard then MUN is not closed".
      "MUN is not closed and there is a blizzard" is not equivalent to any of the others.

4. Let F be a formula $((A \vee (\neg B)) \vee (A \wedge C)) \to (A \wedge (\neg D))$ and G be a formula $((C \to D) \vee ((\neg D) \wedge (\neg C))) \to A$.
   1. How many rows are in a truth table for F? And how many in the truth table for G?
   Answer for F

   F contains 4 variables A, B, C and D, so its truth table has $2^4=16$ rows.

   Answer for G

   G contains 3 variables $A, C and D$, so its truth table has $2^3=8$ rows.

   2. What are the values of F and G when A=True, B=False, C=True and D=True?
      Answer for F

      False

      Answer for G

      True

   3. What are the values of F and G when A=False, B=True, C=True and D=False?
   Answer for F

   True

   Answer for G

   True

   4. Are F and G equivalent?
   Answer

   No. Their values on A=True, B=False, C=True, D=True assignment are different.

Main activity

• A: $(p \wedge \neg q) \to (p \vee q \to \neg q)$
• B: $(\neg q \to p) \wedge (p \to q) \vee (\neg r \to q) $

1. Draw syntax trees for formulas $A$ and $B$ above.
   • Remember the order of precedence: $p \to q \vee r \wedge \neg s$ is fully parenthesized $p \to (q \vee (r \wedge (\neg s)))$.
   Answer for A

   

   Answer for B

   

2. Using your syntax trees, fully parenthesize A and B.
   Answer for A

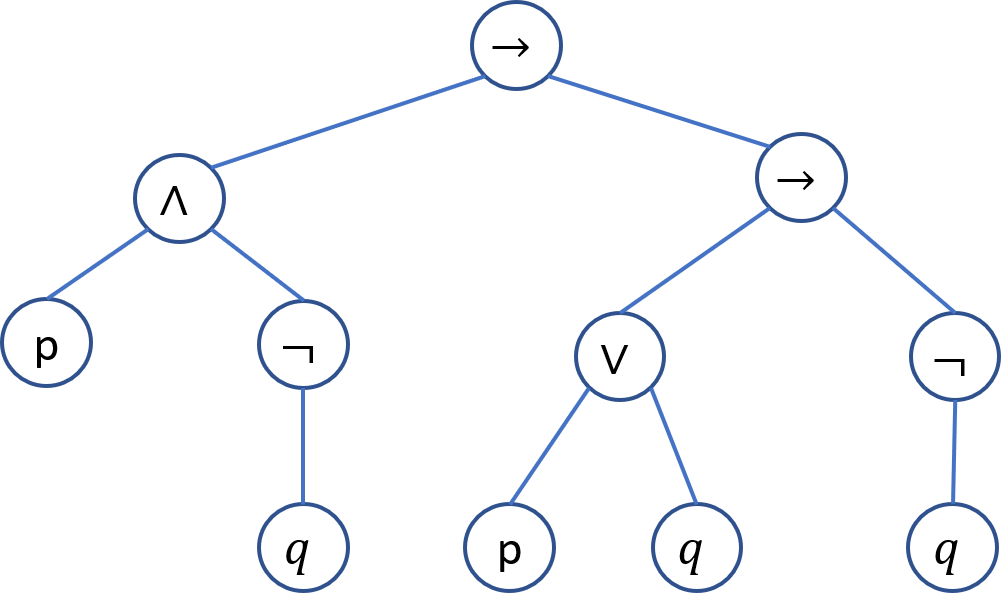
   $ (p \wedge (\neg q)) \to ( (p \vee q) \to (\neg q))$

   Answer for B

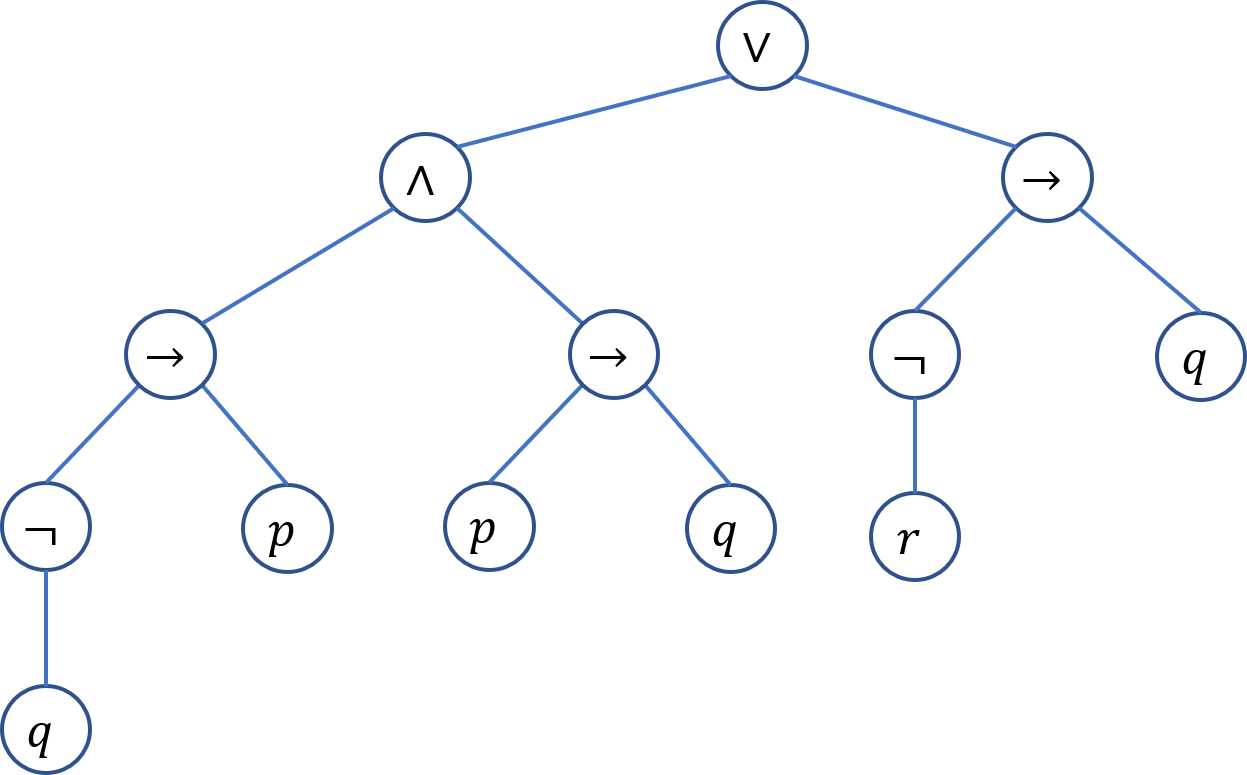
   $( ((\neg q) \to p) \wedge ( p \to q) ) \vee ((\neg r ) \to q )$

3. Fill a truth table for each of these two formulas. Hint: refer to nodes of your syntax trees for intermediate formulas to use as column labels.
   Answer for A

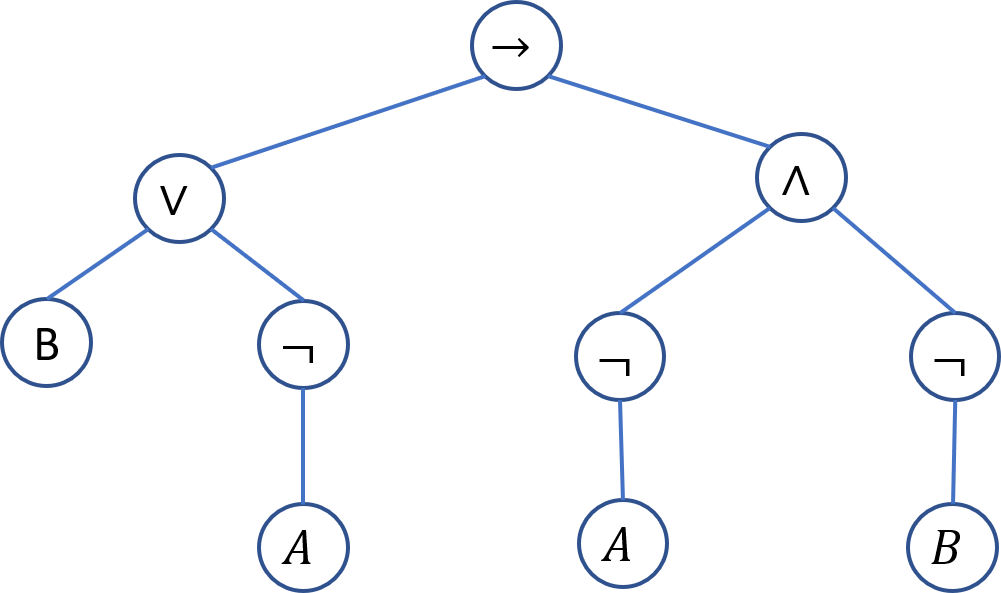
   $p$	$q$	$\neg q$	$p \wedge (\neg q)$	$p \vee q$	$ (p \vee q) \to (\neg q)$	$ (p \wedge (\neg q)) \to ( (p \vee q) \to (\neg q))$
   T	T	F	F	T	F	T
   T	F	T	T	T	T	T
   F	T	F	F	T	F	T
   F	F	T	F	F	T	T

   Answer for B

   $p$	$q$	$r$	$\neg q$	$\neg q \to p$	$p \to q$	$(\neg q \to p) \wedge (p \to q)$	$\neg r$	$\neg r \to q$	$(\neg q \to p) \wedge (p \to q) \vee (\neg r \to q )$
   T	T	T	F	T	T	T	F	T	T
   T	T	F	F	T	T	T	T	T	T
   T	F	T	T	T	T	T	T	F	T
   T	F	F	T	T	T	T	F	T	T
   F	T	T	F	T	T	T	T	T	T
   F	T	F	F	T	T	T	F	T	T
   F	F	T	T	F	F	F	T	F	F
   F	F	F	T	F	F	F	F	T	T

4. Now, go back to the original (parenthesized) formulas A and B, and simplify them as much as you can using equivalences from the table below. Label each step by the name of the equivalence you are using; don't bother to memorize their names.
   Answer for A

   $(p \wedge (\neg q)) \to ((p \vee q) \to (\neg q))$	$\equiv (p \wedge (\neg q)) \to ( \neg (p \vee q) \vee (\neg q)) $	Definition of $\to$
   	$\equiv (p \wedge (\neg q)) \to ( (\neg p \wedge \neg q)\vee (\neg q)) $	De Morgan's law
   	$\equiv (p \wedge (\neg q))\to ( (\neg q) \vee ((\neg p) \wedge (\neg q))) $	Commutativity
   	$\equiv (p \wedge (\neg q)) \to ( (\neg q) \vee ((\neg q) \wedge (\neg p)) $	Commutativity
   	$\equiv (p \wedge (\neg q)) \to ( \neg q) $	Absorption
   	$\equiv \neg (p \wedge (\neg q)) \vee (\neg q) $	Definition of $\to$
   	$\equiv (\neg p \vee \neg (\neg q)) \vee ( \neg q) $	De Morgan's law
   	$\equiv (\neg p \vee q) \vee ( \neg q) $	Double negation
   	$\equiv \neg p \vee (q \vee ( \neg q)) $	Associativity
   	$\equiv \neg p \vee TRUE) $	Definition of TRUE
   	$\equiv TRUE $	Identity

   Answer for B

   $( ((\neg q) \to p) \wedge ( p \to q) ) \vee ((\neg r ) \to q )$	$ \equiv ( (\neg (\neg q) \vee p) \wedge (p \to q) )\vee ((\neg r ) \to q ) $	Definition of $\to$
   	$ \equiv ((q \vee p) \wedge (p \to q) ) \vee ((\neg r ) \to q ) $	Double negation
   	$ \equiv ((q \vee p) \wedge (\neg p \vee q)) \vee ((\neg r ) \to q ) $	Definition of $\to$
   	$ \equiv ((q \vee p) \wedge (q \vee \neg p)) \vee ((\neg r ) \to q ) $	Commutativity
   	$ \equiv (q \wedge (p \vee \neg p)) \vee ((\neg r ) \to q ) $	Distributivity
   	$ \equiv (q \wedge TRUE) \vee ((\neg r ) \to q ) $	Definition of TRUE
   	$ \equiv q \vee ((\neg r ) \to q ) $	Identity
   	$ \equiv q \vee (\neg(\neg r ) \vee q ) $	Definition of $\to$
   	$ \equiv q \vee (r \vee q ) $	Double negation
   	$ \equiv q \vee (q \vee r ) $	Commutativity
   	$ \equiv (q \vee q) \vee r $	Associativity
   	$ \equiv q \vee r $	Idempotence

Here, $p,q,r$ are arbitrary propositional variables (can be substituted with propositional logic formulas). TRUE and FALSE are formulas that are always true and always false, respectively.

Review

Take a formula $(B \vee \neg A ) \to (\neg A \wedge \neg B)$. Now, do all of the following tasks on this formula:

1. Suppose A is "I eat muffins" and B is "I drink coffee". Translate this formula into English.
   Answer

   If I drink coffee or don't eat muffins, then I don't eat muffins and don't drink coffee.

2. Draw a syntax tree for this formula.
   Answer

   

3. Parenthesize this formula fully.
   Answer

   $(B \vee (\neg A)) \to ((\neg A) \wedge (\neg B))$

4. Fill in a truth table for it, noting all intermediate subformulas.
Answer

$A$	$B$	$\neg A$	$B \vee (\neg A)$	$ \neg B $	$ (\neg A) \wedge (\neg B) $	$(B \vee (\neg A)) \to ((\neg A) \wedge (\neg B))$
T	T	F	T	F	F	F
T	F	F	F	T	F	T
F	T	T	T	F	F	F
F	F	T	T	T	T	T

5. Simplify the formula as much as you can. Use the table of equivalences above.
Answer

$(B \vee (\neg A)) \to ((\neg A) \wedge (\neg B))$	$ \equiv (\neg (B \vee (\neg A))) \vee ((\neg A) \wedge (\neg B))$	Definition of $\to$
	$ \equiv ( (\neg B) \vee (\neg (\neg A))) \vee ((\neg A) \wedge (\neg B))$	De Morgan's law
	$ \equiv ( (\neg B) \vee A) \vee ((\neg A) \wedge (\neg B))$	Double negation
	$ \equiv ( A \vee (\neg B)) \vee ((\neg A) \wedge (\neg B))$	Commutativity
	$ \equiv A \vee ((\neg B) \vee ((\neg A) \wedge (\neg B))$	Associativity
	$ \equiv A \vee ((\neg B) \vee ((\neg B) \wedge (\neg A))$	Commutativity
	$ \equiv A \vee (\neg B)$	Absorption