Review:
Countable-uncountable sets
Recall that in Tarski world our structures are boards with pieces on them. We write predicate logic formulas over the signature of five unary predicates (Triangle(), Square(), Circle(), Big(), Little()) and three binary predicates (NextTo(,), Aligned(,), EqualSize(,) ), then for a formula F and board B we determine whether F is true or false on B.
In this lab, let's generalize the notion of Tarski board: rather than having only 5x5 boards, let's have n x n boards for arbitrary integers n. Everything else stays the same: we still have big and little squares, circles and triangles as our pieces.
- How many possible pieces are there in our Tarski world, if there are three shapes (triangles, squares, circles) and each shape is either big or little (but not both)?
- How many possible 1 x 1 boards are there? Hint: a cell in a board can also be empty.
- How many possible 5 x 5 boards are there? Here, you can assume that the cells are numbered: the top-right cell is (1,1), the top-left is (1,5), etc, so you do not need to think about rotating boards. That is, a 5x5 board which contains the a triangle in the top-right corner and nothing else is different from a board which contains a big triangle in the bottom-left corner and nothing else, etc.
- How many n x n boards are there?
- How do you enumerate boards of the same size ( size n x n)? Hint: suppose that all-empty n x n board is number 1 in the list. Enumerate all possibilities for a cell content, and use lexicographic ordering.
- Suppose you have a 2x2 board which contains two big squares in cells (1,2) and (2,2), and a little triangle in the cell (2,1); see below. What would be the index of this board among all 2x2 boards according to the ordering you just described?
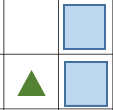
- How many boards of size less than n x n are there? Write the result using summations; do not bother trying to simplify.
- Now, use the results above to show that the set of all Tarski boards is countable. That is, describe a bijection $f$ from the set of all Tarski boards (of arbitrary finite size) to natural numbers. Hint: let the empty 1x1 board be number 1. Describe how will you enumerate all boards using the answers from the previous subquestions.
For every formula (sentence, to be precise), we can talk about the set of (finite) structures (in our case, Tarski boards) on which the formula is true. For example,the formula ∃x Triangle(x) ∧ Big(x) is true on all Tarski boards that have a big triangle in some cell (which is infinitely many boards). Is it also true that for every set of Tarski boards there is a formula which is true on all and only boards from this set? Let's figure it out.
- Rather than counting formulas directly, as we did with Tarski boards, let's show that the set of all predicate logic formulas is countable by using the following claims. Claim 1: an infinite subset of a countable set is countable. Claim 2: a set of strings over a finite alphabet is countable.
Show that every formula over Tarski world signature can be written as a finite string over some alphabet (say which alphabet). Then, explain why these two claims together with your representations of formuas as string let us conclude that set of all predicate logic formulas over Tarski world signature is countable.
- Now, use diagonalization to show that the set of all possible sets of boards (that is, the power set of the set of all Tarski boards) is uncountable. Start by assuming that there is an enumeration of sets of sets of boards, and construct a set of boards which is not in the list.
- With the last two results, answer the question we stated before that: is it true that for every set of Tarski boards there is a formula which is true on exactly this set?
