Review:
Group activity
For this lab, you will be working with a different type of grammar called L-systems (for Lindenmayer systems: Lindenmayer invented them to simulate how plants grow).
An L-system consists of sets of variables, terminals, and rules, as a context-free grammar, plus a "basis" rule called the axiom. However, those rules are applied differently: rather than selecting a single rule to apply at each step, all variables get replaced by expressions corresponding to the rules defining them (we will only have one rule for each variable). More specifically, at the beginning there is just one string, the axiom of the system. Then, at the next iteration, each variable in that string gets replaced by a longer string according to the rules. At the next iteration, each variable in the resulting longer string gets replaced... and the system can be iterated for as many steps as you like.
To visualize the result, we will use the following web app . If it does not work on your device, here is an alternative. There, rather than replacing a variable with a string, think of replacing a line segment with a more interesting pattern, for each line segment in the picture. In these visualizations, the convention comes from turtle graphics: imagine that you are controlling a cursor, which understand the following commands:
- F (could be other variables) means draw a line forward
- + and - mean turn by the corresponding angle (given in the description of the system)
- If a part of the rule is inside square bracket, [ ], then the part after the brackets begins drawing at the same place as the part in brackets started.
In the first app, it is also possible to change the colour of the lines being drawn (by using C0, C1... etc).
Now, we are ready to start the lab.
- To familiarize yourself with l-systems and turtle graphics, lets first consider the following system.
- Angle: 120 degrees
- Axiom: F
- Rule: F=F+F-F
Write the string after one iteration of this system.
- After that,
try drawing one iteration of this system yourself (that is, the string you just obtained).
- Now try drawing the same system with the angle of 90 degrees, for one iteration.
- Write a string corresponding to running this system for two iterations.
- Try drawing this system with 90 degrees angle after 2 iterations, corresponding to the string you just wrote.
- After that, check your answer in the apps (note that they may start drawing from a different direction); you can set the angle and the number of iterations in the corresponding boxes.
- What picture do you get if you change the angle from 90 to 45 degrees, and change your rule to F=F++F--F?
- Now, write strings after 1 and 2 iterations, then run 1, 2, 3 and more iterations of the following system in the app:
- Angle: 60 degrees
- Axiom: F++F++F
- Rule: F=F-F++F-F
This is an example of a famous fractal: Koch snowflake.
- Now, write the string after 1 iteration and run for several iterations in the app for the following system. Remember that [ ] means return to the previous position before starting the next part:
- Angle: 36
- Axiom: F
- Rule: F=F[+FF][-FF]F[-F][+F]F
- For each of the systems above, try to modify them by adding or removing pieces of the axiom and/or the rule, and observing the changes (for 1, 2, and more iterations).
- Let's try writing the strings resulting after 1 and 2 iterations and running the app for one more system, this time using more than one variable. Try running it for up to 15 iterations in the app, and see what happens.
- Angle: 90
- Axiom: FX
- Rule1: X=X+YF
- Rule2: Y=FX-Y
- Finally, suppose that after 1, 2 and 3 iterations you get the following three pictures (in that order). Suppose that the axiom is F, and the angle is 60. What do you think is the rule? Try it in the app to check your answer.
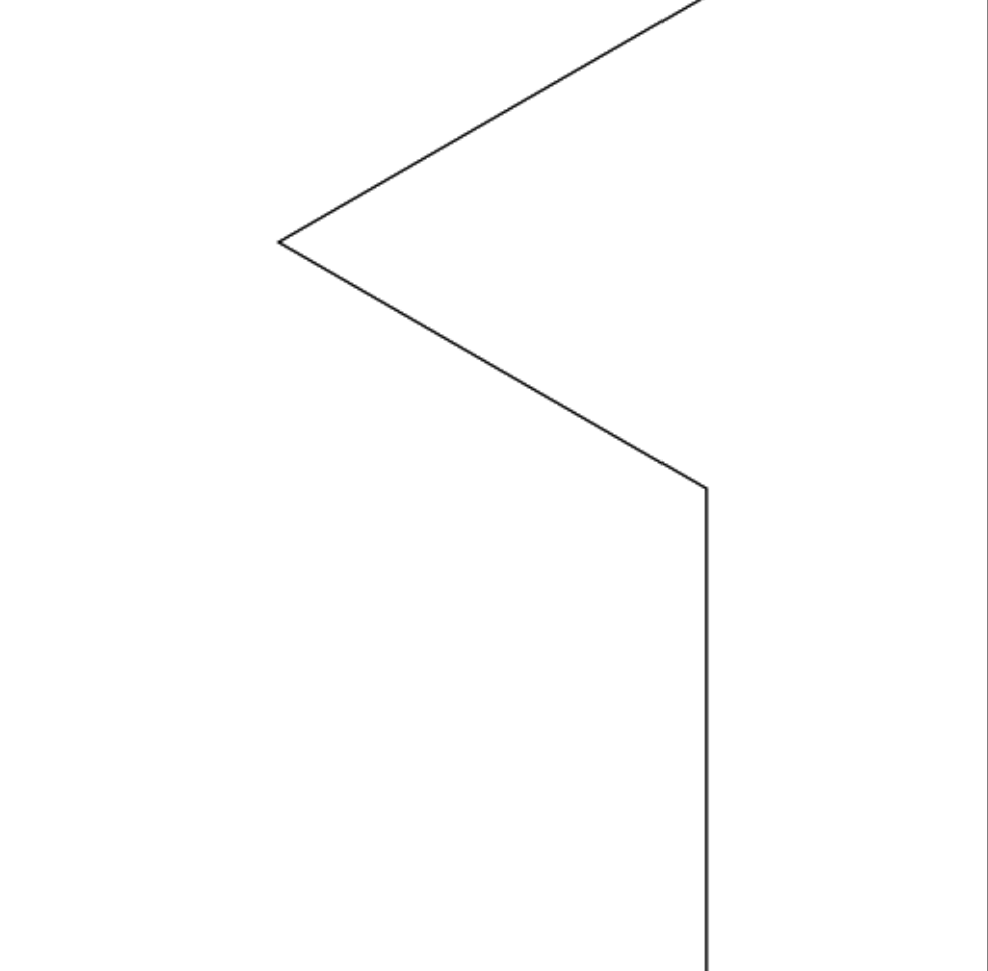
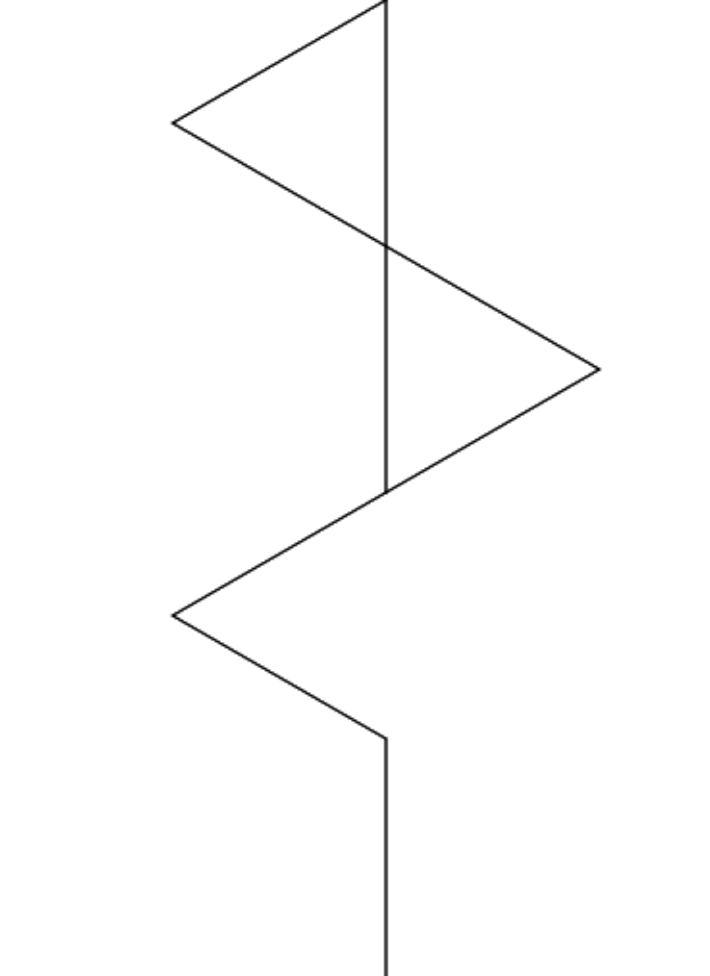
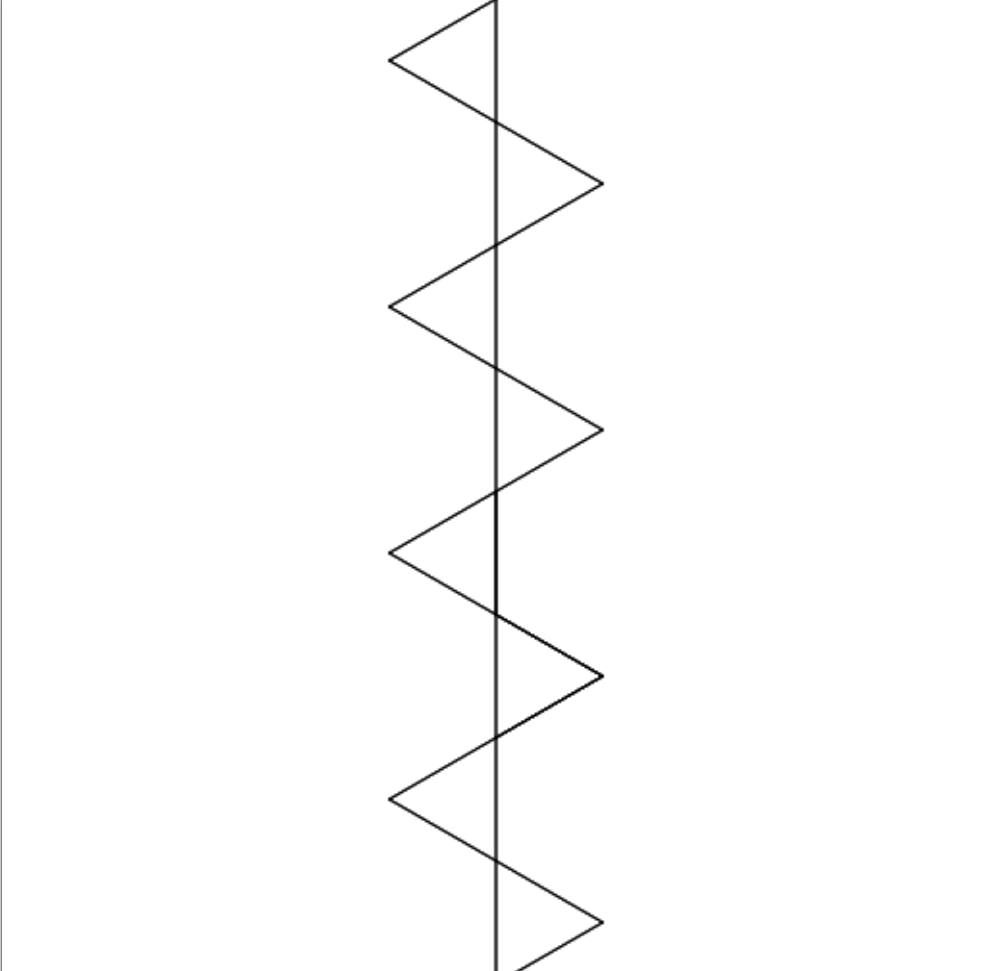
If you have time, look at a few examples provided in the app, and see what grammars they use and what the systems look like after a few iterations.


