Review:
Pythagoras theorem
In this exercise, you will do a direct proof "by picture" of the famous Pythagoras's theorem. Please do not try to read the proof online, it is likely to be more confusing than to figure it out yourself given the steps -- besides, there is a large number of different proofs, and even a similar-looking proof might not be the same one as here.
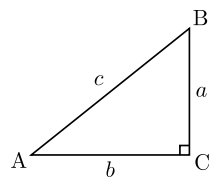 The statement of the Pythagoras' theorem is as follows: for every triangle with a right (90 degrees) angle, the square of the side opposite to the right angle (hypotenuse) is equal to the sum of squares of the other two sides. That is, for every triple of numbers $a,b,c$ labelling sides of a right-angle triangle as in this picture (with c being a hypotenuse), $c^2 = a^2+b^2$.
The statement of the Pythagoras' theorem is as follows: for every triangle with a right (90 degrees) angle, the square of the side opposite to the right angle (hypotenuse) is equal to the sum of squares of the other two sides. That is, for every triple of numbers $a,b,c$ labelling sides of a right-angle triangle as in this picture (with c being a hypotenuse), $c^2 = a^2+b^2$.
- Proof of Pythagoras' theorem
Here is a template for this lab in Google Drawings. As in the previous lab, have one person in your breakout room make a copy of it, and share it with the rest of you breakout room with edit permissions. The first part of the lab involves manipulating the pieces in the template (there is also a second part, about Pythagorean triples; do not forget it).
- You have three squares, of sides $a$, $b$, and $c$, and a triangle with sides $a,b,c$.
- Make 7 more copies of the triangle (so that you have 8 identical triangles).
- Now, make two squares by using the three squares and 8 triangles that you have (see the picture below). You can rotate the triangles by dragging the dot above (when selected).
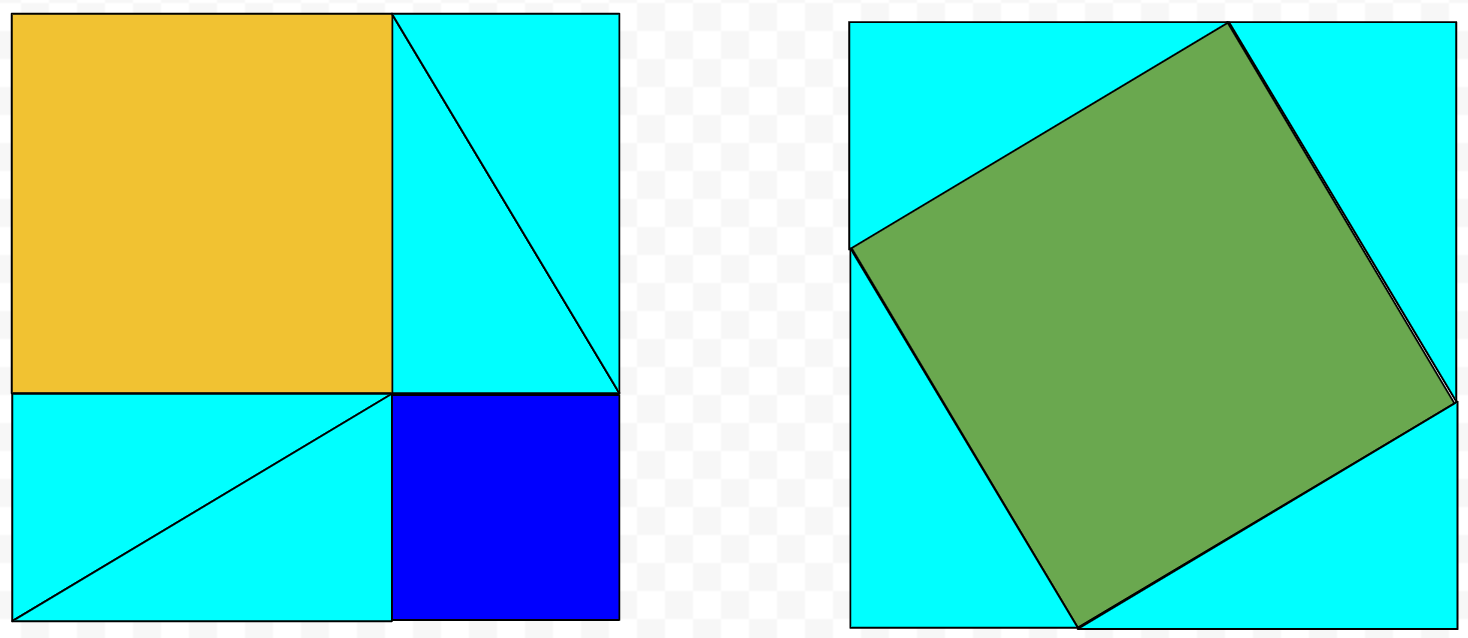
- What are the lengths of the sides of the resulting two squares (in terms of a, b, c)?
- Looking at these two squares can already suggest to you a proof of the Pythagoras' theorem. To make it more formal, write three expressions for the area of the whole square: 1) by using just the lengths of its sides 2) by summing up areas of pieces in first square 3) by summing up the areas of the pieces in the second square. All you need here is that an area of a rectangle is a product of lengths of its sides.
- Now, note that the expressions you obtained in the previous step have to be all equal, since both 2nd and 3rd are equal to the 1st. Write an equality between the 2nd and 3rd expression. Then, subtract the areas taken by the triangles from both sides of this equality.
- You should end up with a formula for Pythagoras' theorem.
- Now, examine the assumptions (if any) you have made in the process. Explain why your proof generalizes to any right triangle. Would it generalize for a triangle which does not have a right angle? Note in particular the selection of a and b. Did they need to be integers? Positive? Was there anything special about them, or could they have been arbitrary?
- Where do you think in your proof you used universal instantiation and generalization? Which definition did you use? Any other rules you can point out?
- Done!
- A Pythagorean triple is any sequence of three natural numbers $a,b,c$ that satisfies the equation $a^2+b^2=c^2$.
- Give two examples of Pythagorean triples
- Based on what you learned from doing the proof of Pythagoras' theorem, can you show that there are infinitely many Pythagorean triples? (Hint: there are several ways of solving this problem. )
Review
Consider the proof of Pythagoras' theorem.
- Use the first picture to derive an expression for opening parentheses in $(a+b)^2$ and a formula for an area of a right triangle in terms of $a$ and $b$
- Suppose a=3 and c=5, where c is a hypotenuse of a right triangle and a, b are the other two sides. What is the value of b? What is the area of the whole square in the proof? And what is the area of a triangle with sides $a,b,c$?
- Give two more examples of Pythagorean triples.
 The statement of the Pythagoras' theorem is as follows: for every triangle with a right (90 degrees) angle, the square of the side opposite to the right angle (hypotenuse) is equal to the sum of squares of the other two sides. That is, for every triple of numbers $a,b,c$ labelling sides of a right-angle triangle as in this picture (with c being a hypotenuse), $c^2 = a^2+b^2$.
The statement of the Pythagoras' theorem is as follows: for every triangle with a right (90 degrees) angle, the square of the side opposite to the right angle (hypotenuse) is equal to the sum of squares of the other two sides. That is, for every triple of numbers $a,b,c$ labelling sides of a right-angle triangle as in this picture (with c being a hypotenuse), $c^2 = a^2+b^2$.
