Linguistics 6800, Winter '06
Course Diary

---

Copyright 2006 by H.T. Wareham
All rights reserved

---

Week 1, Week 2, Week 3, Week 4, Week 5, Week 6,
Week 7, Week 8, Week 9, Week 10, Week 11, Week 12,
(end of diary)

Tuesday, January 17 (Lecture #1)
[Nederhof (1996); Class Notes]

• Overview of course
  • Basic NLP tasks: recognition, generation, transformation
  • Each of these tasks, whether relative to some linguistic theory or a real-world NLP implementation, is done relative to some sort of mechanism.
  • There may be many types of mechanisms for a particular task; choose among these based on notions of (descriptive) adequacy, mechanism simplicity, and (implementation) efficiency.
  • We will look at various finite-state mechanisms for NLP tasks.
• Focus first on recognition and generation problems; these problems can be implemented by finite-state acceptors. Later on, when we talk about transformation problems, we will look at transformation problems, which are implemented by finite-state transducers.
• Finite-State Acceptors
  • Acceptors operate on languages.
  • Languages and language operations.
    • Concatenation
    • Grouping (Union)
    • Repetition (Kleene Star)
    • Subtraction
    • Intersection
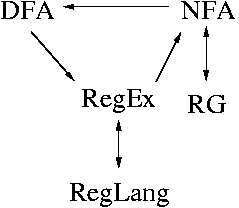
  • Several types of finite-state acceptors:
    • Regular expressions
    • Finite-state machines (FSM)
    • Regular grammars
  • Start by examining these acceptors and how they can recognize and generate individual languages; then we will look at how these acceptors can be combined to implement multi-language operations.
  • Regular Expressions
    • Originated in mathematics community.
    • Algebra over strings with three operations: concatenation, union, and Kleene star.
    • The languages that are accepted by regular expressions are the regular languages.
  • Finite-State Machines
    • Originated in the Engineering community; inspired by the discrete finite neuron model proposed by McCoullough and Pitts in 1943.
    • Overview

Thursday, January 19 (Lecture #2)
[Nederhof (1996); Class Notes]

• Finite-State Acceptors (Cont'd)
  • Finite-State Machines (Cont'd)
    • Also known as finite-state automata (FSA).
    • Basic Terminology: (start / finish) state. transition, configuration, acceptance.
    • Operation (recognition / generation)
      • What happens if there is no transition?
        • Total vs. partial FSM.
    • Types of machines:
      • Deterministic (DFA)
      • Non-Deterministic [transition ambiguity / epsilon-moves] (NFA)
        • Revised notion of string acceptance; see if there is any path through the NFA that accepts the input string.
      • DFA can recognize strings in time linear in the length of the input string, but may not be compact; NFA are compact but may require time exponential in the length of a string to recognize that string (need to follow all possible computational paths to check string acceptance).
    • Oddly enough, deterministic and non-deterministic FSA are equivalent in recognition power!
      • Determinization algorithm (HMU01, Section 2.5.5)
        • Algorithm overview
          • Create state powerset
          • Establish start and finish states
          • Remove epsilon-moves
          • Remove ambiguity
        • Creates DFA from n-state NFA in O(n^32^n) time and O(2^n) space (the latter can add up).
      • DFA produced by this algorithm can be very exponentially larger (in terms of # states) than the input NFA (HMU01, Section 2.3.6).
      • Minimization algorithm (HU79, pp. 67-71)
        • Algorithm overview
        • Creates minimal DFA from n-state DFA operating over alphabet with s symbols in O(sn^2) time; this is, however, potentially still exponential time if the input DFA was created by the determinization algorithm above.

Tuesday, January 24 (Lecture #3)
[Nederhof (1996); Class Notes]

• Finite-State Acceptors (Cont'd)
  • Regular Grammars (RG) (HU79, Section 9.1)
    • Also known as right/left-linear grammars.
    • Originated in the Linguistics community; proposed by Chomsky as the lowest level of the Chomsky Hierarchy of grammars (Regular / Context-Free (Phrase Structure) / Context-Sensitive / Unrestricted)
    • Overview
    • Basic terminology: (production) rule, terminal non-terminal
    • Operation (recognition / generation)
    • Equivalence of FSA and Regular Grammars
      • FSA -> Regular Grammars
      • Regular Grammars -> FSA
  • Relationship of finite-state acceptors (HMU01, Section 4.3.1)
    • Can transform any DFA into a regular expression
      • Creates a regular expression from an n-state DFA in O(n^34^n) time and space.
    • Can transform any regular expression into a NFA
      • NFA constructions for concatenation, union, and Kleene star (HMU01, Section 3.2.3)
      • Creates O(n)-state NFA from n-symbol regular expression in O(n) time and space; however, this NFA must then be made deterministic, which requires exponential time and space in the worst case ...
    • Relationship summary:
      
      
      

Thursday, January 26 (Lecture #4)
[Nederhof (1996); Class Notes]

• Finite-State Acceptors (Cont'd)
  • Combining finite-state acceptors to implement language operations
    • Focus here on finite-state machines.
    • Re-use regular expression -> NFA transformations described above to implement language concatenation, grouping, and repetition!
    • Intersection (HMU01, pp. 134-137)
      • Algorithm overview (state cross-product)
      • Can create an mn-state intersection DFA from input m- and n-state DFAs in O(mn) time and space.
      • Beware cascading intersections! Intersecting k n-state DFA requires O(n^k time and space by this algorithm and there is strong evidence that there is no significantly faster algorithm than this (Finite State Automata Intersection is PSPACE-complete (Garey and Johnson (1979), Problem AL6, p. 266))
    • Subtraction (HMU01, p. 137)
      • Rephrase in terms on language complement and intersection: L1 - L2 = L1 intersect not(L2)
      • Construction for language complement
• Finite-State Transducers
  • Transducers operate on relations.
  • A relation exists between the strings of a pair of languages; in this course, we will be interested in rational relations, in which the two languages are both regular.
    • The two languages are referred to as input / output or lower/ upper -- however, this implies there is a direction (or rather, a directional preference) associated with the relation.
    • Note that the alphabets of the two languages need not be the same, or even have a non-empty intersection.
  • A relation perhaps most naturally viewed as specifying how the inputs of a rule are related to its outputs; however, relations themselves do not encode a notion of rule direction, and (depending on the mechanisms that implement them) can be "run" in either direction.
  • Relation operations
    • Concatenation
    • Union
    • Repetition
    • Intersection
    • Composition
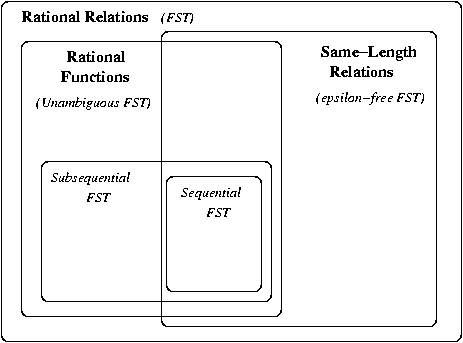
  • There are several types of finite-state relations, which differ in string-pair structure.
    • Rational relations
    • Rational functions
    • Same-length relations
    There are additional types of relations which differ in how easy they are to implement, e.g., (sub)sequential functions.

Tuesday, January 31 (Lecture #5)
[Nederhof (1996); Class Notes]

• Finite-State Transducers (Cont'd)
  • In addition to the problems of string-pair recognition and generation, we now have the problem of reconstruction -- that is, given a string on one side of the relation, what is the set of strings associated with that string on the other side of the relation?
    • Corresponds to applying a rule to an input to get an output, or figuring out what inputs are associated with an output by a rule -- lexical -> surface and surface -> lexical form-transformations, anyone?
  • Several types of finite-state transducers:
    • (Extended) regular expressions
    • Finite-state machines (FST proper)
    • Rules
  • Start by examining these transducers and how they can recognize, generate, and reconstruct individual relations; then we will look at how these transducers can be combined to implement multi-relation operations.
  • Extended Regular Expressions
    • View a string-pair member of a relation as a sequence of symbol-pairs drawn from extended alphabets, .i.e., alphabets augmented by epsilon.
    • Algebra over symbol-pair sequences with three operations: concatenation, union, and Kleene star.
    • The relations that are accepted by extended regular expressions are the rational relations.
    • Operation: recognition / generation pretty standard, but not obvious how one does reconstruction.
  • Finite-State Machines (FST proper)
    • Overview
    • Operation: recognition / generation of string-pairs; reconstruction of output (input) string associated with given input (output) string.
    • Types of FST
      • Encoding same-length relations
        • epsilon-free
        • i/o-deterministic
      • Encoding rational functions
        • unambiguous
        • sequential (i-deterministic)
        • (p-)subsequential
      • Associating weights with string-pairs
        • weighted (see Mohri, Pereira, and Riley (2002) and references)
    • Relationship of relation-types and FST:
      
      
      

    • As there are several types of FST determinism, there are several types of FST non-determinism. In the case of i-determinism, it is known that an FST X encoding a rational functions is i-determinizable iff X has an equivalent subsequential FST; moreover, an FST X encoding a rational relation is i-determinizable iff X has an equivalent p-subsequential FST that satisfies the twins property (Allauzen and Mohri (2002)). These determinizations are done by variations on the standard FSA determinization algorithm and also require exponential time and space in the worst case.
    • Minimization algorithms are also known for particular classes of FST.
  • Rules
    • There are many syntactic variants of rule-formalisms for encoding finite-state transducers. As these are application-specific, we will cover these as we look at various applications later in the course.

Thursday, February 2

• University closed by blizzard; class canceled

Tuesday, February 7 (Lecture #6)
[Kaplan and Kay (1994); Class Notes]

• Finite-State Transducers (Cont'd)
  • Combining finite-state transducers to implement relation operations
    • Focus here on finite-state machines (FST proper).
    • Implement concatenation, union, and Kleene star by non- or fewer-epsilon versions of classical constructions (Kaplan and Kay (1994), Section 3.2).
    • Intersection (Kaplan and Kay (1994), Section 3.3)
      • Algorithm overview (state cross-product; almost identical to classical FSA intersection alg except uses transition symbol-pair rather than transition symbol label identity)
      • Can create an mn-state intersection FST from input m- and n-state FSTs in O(mn) time and space; however, is only guaranteed to work if input FST are both same-length FST.
      • Again, beware cascading intersections! There is strong evidence that there is no efficient algorithm for this problem (Same-length FST Intersection is NP-hard (Barton, Berwick and Ristad (1987), Chapter 5; Wareham (1999), Section 4.4.2; Wareham (2002), Theorem 10)
    • Subtraction
      • As complementation is not defined for FST, cannot re-use the classical FSA subtraction construction in terms of intersection; however, there is a direct construction for the subtraction FST of two same-length FST (Kaplan and Kay (1994), Section 3.3).
        • Composition (Kaplan and Kay (1994), Section 3.2)
        • Algorithm overview (state cross-product; almost identical to FST intersection alg except uses identity of outer and inner symbols of first and second FST transition symbol-pairs )
        • Can create an mn-state composition FST from input m- and n-state FSTs in O(mn) time and space.
        • Again, beware cascading compositions! There is strong evidence that there is no efficient algorithm for this problem (i/o-deterministic FST Composition is NP-hard (Wareham (1999), Section 4.3.2; Wareham (2002), Theorem 12)
• Combining finite-state acceptors and transducers in natural language processing: The big picture (Beesley and Karttunen (2003), Sections 1.7-1.8)
  • NLP system: Lexicon + lexical / surface transformations
    • Lexical form = proto-phonemes + lexical markers
    • Surface form = phone-sequence
  • Three major ways of specifying lexical / surface transformations:
    • Ordered set of rules, e.g., SPE generative phonology rule cascade.
    • Intersection of lexical /surface form constraints e.g., the KIMMO system (see Barton, Berwick, and Ristad (1987), Chapter 5, and references), Declarative Phonology.
    • Ordered set of Optimality-Theoretic (OT) lexical / surface constraints.
  • Can implement these transformations using FST and various FST combination operations!
    • Ordered Rules: Individual rule = FST, compose rule FST in specified order.
    • Intersected Constraints: Individual constraint = FST, intersect constraint FST in arbitrary order.
    • OT Constraints: Individual constraint = FST, leniently compose FST in specified order + extra FST for (finite #) mark counting (Karttunen (1998)).
  • Turn lexicon FSA into FST by replacing each transition label x with x/x, e.g., the identity FST associated an FSA, and then compose this lexicon FST with the lexical / surface transformation FST to create a lexical transducer (Beesley and Karttunen (2003), Section 1.8).
    • Note as FST are bidirectional, so are lexical transducers; hence, can reconstruct surface or lexical forms from given lexical or surface forms with equal ease.
    • Creating this lexical transducer (and applying determinization and minimization algorithms to it) will take exponential time and space in the worst case; however, once it is done, surface and lexical forms can be processed very efficiently (in time proportional to the length of the given surface or lexical form).

Thursday, February 9 (Lecture #7)
[Karttunen (2000); Class Notes]

• Implementing Finite-State Linguistics Systems
  • Four options:
    • Code it yourself (FSM algorithms / data structures from FS literature)
    • FSM code libraries, e,g., Allauzen et al (2004), Mohri, Pereira, and Riley (2000), Watson (1999).
    • FS development environments, e.g., xFST (Beesley and Karttunen (2003))
    • Linguistic system environments, e.g., multilingual text-to-speech development systems (Rojc and Kacic (2003))
  • Increasing ease of use (ascending); increasing flexibility / efficiency(descending).
  • When starting a FS project, be honest about development personnel needs and abilities and select the appropriate level.
• The xFST Finite-State Development Environment: An Overview (Beesley and Karttunen (2003); Karttunen (2000))
  • Consists of a number of programs (xFST, lexc, lookup, tokenize, twolc) -- focus on xFST interface.
  • xFST is a command-line interface; FSM (both FSA and FST) are specified as (extended) regular expressions; can be easily manipulated or interrogated using standard FS operations; has import / export capabilities; all created FSM are automatically determinized and minimized.
  • xFST extended regular expression syntax includes all standard operations as well as a number of "shorthand" operators that do not extend the expressive power but are particularly convenient for computational linguists, e.g., containment, replace, restriction, marking.
  • Suggested principles for FS project operation
    • Treat FS system development as a software engineering project -- proper specification and design procedures are essential.
    • Make sure the underlying formal linguistic analysis is done before codings starts and this analysis is done well -- no development environment can save an inadequate or badly-done analysis from creating an inadequate, poorly-functioning FS system.

Tuesday, February 14 (Lecture #8)
[Class Notes]

• Finite-State Applications
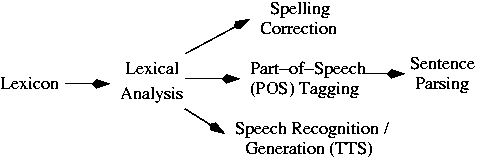
  • What are the opportunities for finite-state methods in Natural Language Processing (NLP)? The following diagram lays out the relationships between a core set of NLP tasks:
    
    
    
    
    
    Each of these tasks has finite-state implementations; we will examine each of them in the remainder of this course, starting with the most basic, the construction and manipulation of lexicons.
  • Building Robust and Efficient Lexicons
    • What is a lexicon?
      • lexicon = forms (morphemes) + associated information, e.g., syntactic role + semantics + phonological base + statistical occurrence specifications.
      • Basic forms are altered by combination with other forms (morphotactics; continuum from inflections / conjugations to compound words to full agglutinating / polysynthetic constructions) and (phonologic / syntactic conditioned) alternations.
      • Note that each underlying form of a word has a unique surface form but that each surface form may have many surface forms, e.g., "run" (noun / verb); hence, lexical / surface forms have an implicit many-one mapping.
    • Focus first on storage of basic forms and their associated information; we will then discuss storage of more complex forms, which will incorporate derivation / alternation processes and hence lead into lexical analysis.
    • Storing basic forms
      • Three options
        • List
        • Trie (= retrieval tree)
        • Deterministic acyclic finite automaton (DAFA)
      • Create trie by compacting list; create DAFA by compacting / minimizing trie.
      • All known algorithms for creating tries and DAFA run in low-order polynomial time (and access to individual words can be done in time linear in the size of the word of interest, regardless of the size of the trie or DAFA); however, tries can be too large for computer memory for even moderate-size applications.
        • Solution: incremental algorithms (on sorted / unsorted word-lists) which simultaneously create and minimize DAFA as they add words one at a time! (Daciuk et al (2000))
        • Incremental algorithms are not quite the fastest known algs but they are close; moreover, given their minimal memory requirements, are the most practical. (Daciuk (2002))
    • Storing basic forms + associated information
      • Five options
        • List with entries "form + info"
        • Trie with info encoded in final states
        • DAFA with info encoded in final states
        • Index-generating DAFA + subsidiary info arrays
        • FST relating form x info pairs
      • First three options progressively more compact; however, even third option is problematic if # discreet forms of info is not a small finite-set, e.g., syntactic-role vs. semantic info.
      • Fourth option made possible by creating turning DAFA into numbered DAFA, which can then be interpreted as perfect hash automata. (Lucchesi and Kowaltowski (1992); see also Grana et al (2001) and references)
        • Construction of the numbered DAFA associated with a DAFA can be done in time linear in the size (states + transitions) of the given DAFA.
        • Give such a numbered DAFA, generating the index associated with a word can be done in time linear in the length of the word; oddly enough, generating the word associated with an index can also be done in linear time!
      • Fifth option possible relative to subsequential transducers (Mohri (1996); Mihov and Maurel (2000)).
        • Original proposal creates and then determinizes / minimizes this transducer; as intermediate FST size is large, lexicon created by creating sublexicon FST and then doing the deterministic union to create the full lexicon FST (sound like the original DAFA (trie + minimization alg, anyone?) (Mohri (1996))
        • Subsequent proposal adapts incremental DAFA creation algorithms to directly create minimized FST without intermediate FST memory overhead (Mihov and Maurel (2000)).
        • None of these algorithms has associated time/ space complexities stated in the literature, only experimental results with implementations -- is probably still room for improvement.

Thursday, February 16 (Lecture #9)
[Beesley and Karttunen (2003); Class Notes]

• Finite-State Applications (Cont'd)
  • Building Robust and Efficient Lexicons (Cont'd)
    • Storing complex forms
      • Focus here on complex forms generated by morphotactics / derivation processes.
      • Problems that need to be handled (Beesley and Karttunen (2003), Sections 7.3.1 and 8.3):
        • Adjacent dependencies, e.g., English verb tense / person marking
        • Non-adjacent dependencies, e.g., Arabic prefix / suffix co-occurrence
        • Interdigitation, e.g., Arabic stem transformation
        • Reduplication, e.g., Malay plural formation
      • Morphotactic models:
        • Finite-state (continuation classes)
        • Rule-based
        • Unification-based, e.g., Ritchie et al (1992).
        • Multi-tape finite-state (see Kiraz (2000) and references)
      • The xFST solution: (syntactically) extended finite-state
        • lexc: An overview (Beesley and Karttunen (2003), Chapter 4)
          • lexc encodes the finite-state continuation-class model
          • Can have continuation-class loops
        • lexc strategies for irregular forms (Beesley and Karttunen (2003), Section 5.4)
          • Brute force (x:y)
          • Priority union
        • So, lexc can nicely handle basic adjacent-dependency morphotactics and grossly irregular forms -- what about more complex morphotactics? This will be the subject of our next lecture.

Tuesday, February 21

• Midterm break; no lecture

Thursday, February 23

• Midterm break week; lecture canceled

Tuesday, February 28

• Lecture canceled

Thursday, March 2

• University closed by blizzard; lecture canceled

Tuesday, March 7

• Student Presentations #1
  • Alegria, I. et al (2001) "Using Finite State Technology in Natural Language Processing of Basque." In CIAA 2001. Lecture Notes in Computer Science no. 2494. Springer-Verlag. 1-12. [PDF] (Presented by R. Keating)
  • Kiraz, G.A. and Mobius, B. (1998) "Multilingual Syllabification Using Weighted Finite-State Transducers." [PDF] (Presented by D. Graham)

Thursday, March 9

• Instructor sick; lecture canceled

Tuesday, March 14 (Lecture #10)
[Beesley and Karttunen (2003); Class Notes]

• Finite-State Applications (Cont'd)
  • Building Robust and Efficient Lexicons (Cont'd)
    • Storing complex forms (Cont'd)
      • The xFST solution: (syntactically) extended finite-state (Cont'd)
        • lexc strategies for very complex forms
          • Over-generation + lexical-side filters
          • Flag diacritics (restricted unification) (Beesley and Karttunen (2003), Chapter 7)
          • The compile-replace operation (Beesley and Karttunen (2000); Beesley and Karttunen (2003), Chapter 8)
        • Odd as it may seem, none of these new mechanisms extend the expressive power of the xFST system beyond the regular relations its standard features encode (Beesley and Karttunen (2003), Section 8.6); rather, they allow for more succinct expression and compact storage of FST.
    • Storing complex forms + associated information
      • If using finite-state scheme to handle complex forms, can adapt options (3)-(5) for simple forms + associated information.
      • Option (5) (transducer-based) perhaps most natural, and is that encoded in xFST; however, restricts associated info to tags encoded in lexical forms.
    • Now that we can generate morphotactically complex forms and store associated information, focus on how we complete the lexicon by encoding alternation.
      • Many distinct formalisms proposed over the years (SPE rewrite rules, two-level rules (KIMMO), Declarative phonology and Optimality Theory constraints); however, all of these have FST implementations! (see Kaplan and Kay (1994) and Wareham (1999) and references).
      • Can use composition to bind basic lexicon (filter + overgeneration) FST and alternation FST to create full lexicon FST.
    • Though the finite-state framework is a tad constricting in places (especially wrt the auxiliary information that can be easily associated with a lexical form), it does provide a unified and standard methodology for creating and using lexicons. Moreover, it also provides easy integration of lexicons with other finite-state implementable applications.
    • The xFST solutions outlined above (in particular, flag diacritics and the compile-replace operation) allow efficient implementation of particular linguistic phenomena but are not motivated by or included in classical linguistic description or theory, cf., Kiraz (2000) and Ritchie et al (1992). One can argue that it may be more natural to use standard linguistic formalisms to specify these phenomena, and then to compile these formalisms into their associated efficiently-realizable finite-state mechanisms (as is done fully in Kiraz (2000) and partially in Ritchie et al (1992)). Such a process underlies efficient "transparent" transformational syntax parsing systems (Berwick and Fong (1995)).

Thursday, March 16 (Lecture #11)
[Beesley and Karttunen (2003); Class Notes]

• Finite-State Applications (Cont'd)
  • Lexical Analysis (Sections 9.3 and 9.5, Beesley and Karttunen (2003))
    • Analysis of lexicon-encoded known forms
      • Run lexical transducer in reverse on surface form to derive associated lexical form.
      • If there are several language-variants, can run surface form against each of the associated lexical transducers until one succeeds.
    • Analysis of lexicon-encoded known forms + unknown forms
      • Unknown forms are typically those in which a root unknown to the lexicon has been acted on by lexicon-encoded morphotactics.
      • Create "guesser" transducer which encodes standard morphotactics but in which root forms are replaced by a sub-transducer that recognizes all phonologically-possible roots in the language on the surface side and adds a special lexical tag, e.g., +guess, on the lexical side.
      • If a given surface form is not recognized by the known-form lexical transducer, run it against the guesser transducer to extract potential roots; these can then be presented to the user for validation and possible addition (via union) to the known-form lexical transducer.
    • Complications:
      • Lexical transducers may be too large to fit in memory; this occurs particularly in cases of language variation in which language-variant lexical transducers are created by composition of a subset of component transducers.
      • Implementing the "run until success" procedure for a surface form relative to a group of lexical transducers can be intricate and possibly prone to coding error.
    • Lexical analysis in xFST
      • Constructing guesser transducers (Section 9.5.4, Beesley and Karttunen (2003))
        • General strategy:
          • Add guessed-form "placeholder" tag entries to the various root sub-lexicons to create an augmented lexical transducer.
          • Define possible root form transducers for each of the roots.
          • Define a new lexical transducer by substituting the possible-root form transducers for the guessed-form root tags in the augmented lexical transducer.
        • Implement the third of these steps using the substitute command (which is a restricted form of the compile-replace operation).
      • Lexical analysis via the lookup program
        • Syntax overview: transducer definitions + transducer application strategy.
        • Does not actually perform compositions but simulates them at run-time; runs slower but can save dramatic amounts of memory.
        • Assumes root+tags lexical-form structure.
        • Output overview.

Tuesday, March 21 (Lecture #12)
[Beesley and Karttunen (2003); Class Notes]

• Finite-State Applications (Cont'd)
  • Spelling Checking and Correction
    • Characteristics of word misspelling
      • Based on four types of errors: single symbol insertion / deletion / substitution or adjacent symbol transposition (Damerau (1964)).
      • Vast majority of misspellings involve only one error, e.g., approx. 2% of unknown words in a corpus due to multiple-error misspellings (Ren and Perrault (1992), cited on page 253 of Savary (2002)).
      • The number of possible correct words increases dramatically as number of possible errors increases, e.g., O(n^k) possible corrections for a word of length n created by k errors.
    • Spelling checking
      • Goal is to determine whether or not a given word is misspelled.
      • Can be done relative to the surface-form automaton associated with a standard lexical transducer; if the given surface form does not have an associated lexical form, it is misspelled.
    • Spelling correction
      • Goal is to find list of candidate correct words for a given misspelled word; choice of correction is then left to the user.
      • Simplest scheme envisions each possible type of error as an optional rewrite rule; the transducers associated with these rules are composed with the surface-form automaton associated with a standard lexical transducer, and a given word is associated with all words that can be created from it by any sequence of errors (Section 9.6, Beesley and Karttunen (2003)).
        • Is a straightforward, purely finite-state implementation of Damerau (1964); has been used in many finite-state systems, e.g., the Xuxen spelling correction system for Basque (see Alegria et al (2001) paper presented by Keating).
        • There are several major difficulties with this approach -- namely, ordering the rewrite rules to take into account even the most elementary multi-error misspellings is difficult, and returned candidates are not ordered in any sensible way, e.g., by number / probability of errors invoked.
      • More complex schemes explicitly compute and rank candidates related by multiple spelling errors; to do this, three things must be specified:
        • Measure of spelling error distance between two words, e.g., Levenshtein / edit and weighted edit distance (see Section 4 of Kruskal (1984) and references), error distance (Du and Chang (1992)).
        • Degree of maximum allowable spelling error (distance threshold).
        • Type of correction list ((ordered) exhaustive vs. nearest neighbor).
          • Nearest neighbor approaches suffice in many applications, as long lists of candidates are both hard to compute and discouraging for users to sort through (Savary (2002), p. 253).

Thursday, March 23 (Lecture #13)
[Class Notes]

• Finite-State Applications (Cont'd)
  • Spelling Checking and Correction (Cont'd)
    • Spelling correction (Cont'd)
      • Sample algorithms:
        • Oflazer (1996) [error distance / arbitrary threshold / exhaustive]
          • Depth-first search on lexical transducer, with pruning relative to cut-off error distance.
          • On corpus of 3000 misspelled Turkish words, correct form had distance 2 in 15% of the cases, and correct form had distance >= 3 in 5% of the cases (not due to word length, average of which was ~10 symbols), cf., Ren and Perrault (1992).
        • Mihov and Schulz (2004) [Levenshtein / edit distance / arbitrary threshold / exhaustive]
          • Parallel depth-first search on lexical transducer and universal Levenshtein automaton.
        • Savary (2002) [error distance / arbitrary threshold / nearest neighbor]
          • Depth-first search in lexical transducer with dynamic pruning.
          • Keep track of minimum error distance with counter; avoids dynamic-programming calculation of error distance.
          • Runs in O(|w|^{t + 1}f^t)) time and (|w|f) space, where |w| is the length of the misspelled word, t is the error threshold, and f is the maximum transition fanout of any state in the lexical transducer.
        • Vilares et al (2004, 2005, 2006) [error distance / arbitrary threshold / nearest neighbor]
          • Depth-first search in lexical transducer with dynamic pruning.
          • Exploit topological structure of lexical transducer to limit depth / type of both lookahead and backtracking on detecting error.
          • Same asymptotic worst-case performance as Savary (2002), but much better performance in practice.
      • Oddly enough, there is a parallel and independent algorithmic tradition of this problem in formal language theory!
        • Wagner (1974) [Levenshtein / edit distance / -- / nearest neighbor]
          • Dynamic programming algorithm.
          • Runs in O(|w||Q|^2)) time and (|w||Q|) space, where |w| is the length of the misspelled word and |Q| is the number of states in the lexical recognizer.
        • Myers and Miller (1989) [Levenshtein / edit distance / -- / nearest neighbor]
          • Dynamic programming algorithm.
          • Runs in O(|w||R|)) time and (|w||R|) space, where |w| is the length of the misspelled word and |R| is the number of symbols in the in the regular expression encoding the lexical recognizer.
        • Kari et al (2003) [weighted edit distance / -- / nearest neighbor]
          • Model as finding the shortest accepted string in the intersection of the lexical recognizer and a special weighted finite-state e-automaton.
          • For edit distance and acyclic lexical recognizer, runs in O(|w||Q|)) time and space, where |w| is the length of the misspelled word and |Q| is the number of states in the lexical recognizer.
        • Note that though each of these algorithms supports arbitrary distance thresholds, the increase in candidate-set size with threshold typically limits thresholds to values less than 4 in practice; however, given the statistical rarity of multi-error misspellings, this is frequently sufficient.
      • Occasionally, there is replication of results within these parallel streams of literature, e.g., Mohri (2003) is a parallel derivation of results in Kari et al (2003) within the weighted finite-state framework.
  • Despite all our algorithmic sophistication, given the incompleteness of encoded lexicons, decisions about whether an unknown form is a new word to be added to the lexicon or a misspelled form of a known word cannot and should not be completely automated, e.g., is [blints] a misspelling of /blink/ [Plural], the plural of a new word /blint/, or a previously unencoded term for a tasty cherry and cream-cheese filled omelette?

Tuesday, March 28 (Lecture #14)
[Class Notes]

• Finite-State Applications (Cont'd)
  • Sentence Parsing
    • Since Chomsky's proof that finite-state grammars were inadequate for certain sentence-level syntactic phenomena, i.e., recursive embedding (see Chapter 3, Chomsky (1962) and references), syntax parsing has focused primarily on higher-level grammar formalisms. However, there are two finite-state approaches to sentence parsing:
      
      
      • Partial Parsing: Recover the largest possible sub-forest of the full parse-tree for a given sentence.
      • Grammar Approximation: Derive a finite state grammar that encodes a sub/superset of the language recognized by a higher-level grammar that encodes the highest possible number of sentences that occur in practice.
      
      Both of these approaches employ part-of-speech (POS) tagger preprocessing which assigns the best possible lexical tags to each word / morpheme in a sentence.
    • Part-of-Speech (POS) Tagging
      • Can theoretically speed up parsing by reducing lexical ambiguity of individual words; however, has been criticized because (1) may only be doing low-level work that is better encoded in the parser and (2) may actually mislead and slow down parser if tagger makes bad guesses.
      • Two finite-state approaches (see Abney (1996) and references):
        • Statistical
          • To assign a tag to a word, look at some combination of the immediately preceding words and their assigned tags; assign most probable tag based on distributions of this preceding information derived from a training set.
          • Encode as Hidden Markov Models (HMM); these can in turn be encoded as the composition of weighted FST (Pereira, Riley, and Sproat (1994)).
          • Training process very easy; however, derived HMM-FST can be very large and slow.
        • Rule-Based
          • Two-phase process: assign initial guess-tags to the words in the sentence and then apply a set of context-based repair rules to fix these initial guesses.
          • First phase can be done using a standard lexicon plus some additional guess-rules for unencoded words; second phase can be done by inferring repair rules relative to a training set by some method, e.g., Brill (1995) and references.
          • All guess and repair rules can be encoded as deterministic (Roche and Schabes (1995)) or weighted (Tzoukermann and Radev (1999)) FST; these can in turn be combined into a single FST using either composition or intersection (see references above).
          • Derived FST are typically smaller than HMM-FST and faster.
      • Just how well do these approaches work?
        • Beware evaluation purely on the basis of how often individual words are tagged correctly -- the goal, after all, is reliable sentence parsing, and a bad tag-guess in a single word can mislead a parser relative to a sentence (Abney (1996)).
        • Experiments show that POS taggers can improve parser accuracy but do not seem to dramatically sped up parsing (Voutilainen (1998)). Moreover, even perfect POS tagging may not help, as up to 30% of actual sentences with different parses have identical POS tag-sequences (Dalrymple (2006)).
        • Additional problems may arise when treating agglutinative languages, in which lexical tags are complex and require very large training sets to produce non-empty distributions of cases (see Hakkani-Tur, Oflazer, and Tur (2002) and Oflazer (2003) and references).
    • Partial Parsing (see Abney (1996) and Oflazer (2003) and references)
      • Implemented by an extended finite-state approach, in which a cascade of FST recreates as many of the layers of constituents in the full parse tree as possible by combining tags into higher-order tags.
      • Can implement as fixed set of "stratum" FST or a master FST that iterates until there is no change in the tag-sequence.
      • Note that the intermediate tag-sequences produced by FST application are the desired output, not the just the final tag-sequence; hence, stratum FST cannot be composed, cf., cascades of morphophonological rules.
    • Grammar Approximation (see Nederhof (2000) and references)
      • There are many methods for constructing finite-state grammars approximating context-free grammars, almost none of which have well-defined time or space complexities. Experiments suggest that superset methods are the fastest and yield the smallest grammars and tightest language-approximations in practice.

Thursday, March 30 (Lecture #15)
[Class Notes]

• Finite-State Applications (Cont'd)
  • Speech Processing
    • Several types:
      
      
      • Speech recognition (acoustic -> lexical / written (orthographic))
      • Speech generation (lexical / written (orthographic) -> acoustic)
      
      Is typically restricted to transforms between written and acoustic forms, i.e., Text-to-Speech (TTS) systems; however, it is useful to keep all four possible transforms in mind (plus the two transforms between the written and lexical forms).
    • Can be construed as a series of relations between forms; as lexical (and often partial discourse, e.g., phrasal boundaries, intonation curve) information may be required, lexical forms may be intermediate (see below).
    • Speech recognition framework (Pereira, Riley, and Sproat (1994)):
      
      
      
      
      
      
      
      • The acoustic model relating acoustic observations and phones typically has several intermediate levels dealing with the various mathematical transformations applied to the raw data, e.g., sequences of audible-frequency energy samples (100 per second).
      • The pronunciation model linking phones and written words also has several levels, one of which is the lexical form.
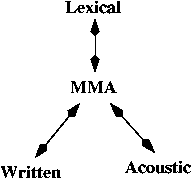
    • Text-to-Speech framework (Sproat (1996)):
      
      
      
      
      
      
      MMA = Minimal Morphologically-Motivated Annotation, i.e, the minimal amount of lexical information required to transform between orthographic and acoustic forms.
      • Subsumes the framework for speech recognition.
      • Are typically only concerned with the written -> acoustic form relation-cascade; however, in principle, there are five other cascades between pairs of end-forms that are of interest in language processing (most of this course, we've focused on the written -> lexical and lexical -> written ones).
      • The lexical -> MMA transform is not trivial; must deal with symbol expansion, e.g., percent signs, numbers, and homographs, e.g. "bass" (fish or musical instrument?)
    • Characteristics of form-relations in these frameworks:
      
      
      • Relations phrased as conditional probabilities
      • During processing, typically require most probable output associated with input
      
      During implementation, these characteristics are the sources of modeling and search errors, respectively.
    • Can implement such form-relations as weighted FST!
      • Weighted FSA are FSA in which each transition now has an associated number, and each path from a start state to a finish state has an associated value equal to the sum of the transition-weights on that path.
        • Can encode products of probabilities as sums of negative log probabilities.
      • The most probable output string associated with a given input string by a weighted FSA corresponds to the shortest accepting path for the given string in that FST => use standard shortest-path algorithms to compute weighted FST functions!
      • Weighted FSA have all standard FSA operations via modifications to standard FSA operation algorithms (Mohri (2004); Mohri, Riley, and Sproat (1996)).
    • Stating relation-operations in speech processing in terms of weighted FST not only places such operations in a simple framework, but also exposes opportunities for optimizations that were not readily available in previous speech processing software (Pereira, Riley, and Sproat (1994)). For example, the straightforward composition of the full set of weighted FST associated with the speech-processing relations described above would typically produce FST that are very large (on the order tens or hundreds of millions of states and transitions). Deal with this in two ways (Mohri, Riley, and Sproat (1996)):
      
      
      • Break full composition cascade into collection of linked cascades creating intermediate weighted FST (lattices) and perform time/ space optimizations on these lattice-FST, e.g., lazy composition, local determinization, path pruning.
      • As optimal shortest-path algorithms run in time cubic in the number of states in the weighted FST, use various shortest-path heuristic algorithms with lower time complexities, e.g., A* / beam search, rescoring.
      
      Note that the latter may introduce search errors resulting in outputs that are not the most probable relative to a given weighted FST cascade.
    • Further complications are introduced by the need to choose between different pronunciation models e.g., Hazen et al (2002); Trancoso et al (2003) (can be treated using decision trees (Mohri, Riley, and Sproat (1996)), which can themselves be encoded as weighted FST (Sproat and Riley (1996)) and the training-set problems associated with processing agglutinative languages, e.g., Oflazer and Inkelas (2003).
    • Note in the discussion above, we assumed that we were operating on acoustic and written forms within the same language; this need not be so! Given suitably-stated weighted FST cascades, can do various types of inter-language translation within this framework,, e.g., Casacuberta and Vidar (2004).
  
  
  
• The final remark above can be broadened further -- assuming we are dealing with linguistic forms that can be encoded as strings over some alphabet and that these sets of strings form regular languages, almost any imaginable transformation between these forms can be encoded using FST along the lines described in this course. The sky is therefore the limit in terms of what linguists can do in the finite-state framework. That being said, one should always keep in mind the computational time and space costs associated with certain finite-state operations (nondeterminism, intersection, composition) and thus try to strike a balance between ease of linguistic phenomena expression and implementation efficiency. Hence ...
  
  
  
  "Let's be careful out there."
  
  - Sgt. Phil Esterhaus, Hill Street Blues
  
  
  
  

Tuesday, April 4

• Lecture canceled

Thursday, April 6

• Student Presentations #2
  • Gerdemann, D. and van Noord, G. (2000) "Approximation and Exactness in Finite State Optimality Theory." In SIGPHON 2000. [PDF] (Presented by D. Graham)
  • Friburger, N. and Maurel, D. (2002) "Finite State Transducer Cascade to Extract Proper Names in Texts." In CIAA 2001 Lecture Notes in Computer Science no. 2494. Springer-Verlag; Berlin. 115-124. [PDF] (Presented by R. Keating)

References

• Abney, S. (1996) "Part-of-Speech Tagging and Partial Parsing." In Church, K., Young, S., and Bloothooft, G. (eds.) Corpus-Based Methods in Language and Speech. Kluwer Academic Publishers; Dordrecht. 118-136. [PDF]
• Allauzen, C. and Mohri, M. (2002) "p-Subsequentiable Transducers." In CIAA 2002. Lecture Notes in Computer Science no. 2608. Springer-Verlag; Berlin. 24-34. [PDF]
• Allauzen, C., Mohri, M., and Roark, B. (2004) "A General Weighted Grammar Library." In CIAA 2004. Lecture Notes in Computer Science no. 3517. Springer-Verlag; Berlin. 23-34. [PDF]
• Beesley, K.R. and and Karttunen, L. (2000) "Finite-state Non-concatenative Morphotactics." In SIGPHON 2000. 1-12. [PDF]
• Beesley, K.R. and and Karttunen, L. (2003) Finite-State Morphology. CSLI Publications; Stanford, CA.
• Berwick, R.C. and Fong, S. (1995) "A quarter century of computation with transformational grammar." In J. Cole, G M. Green, and J.L. Morgan, eds., Linguistics and Computation. CSLI Lecture Notes no. 52. CSLI Publications, Stanford, CA. 103-143.
• Brill, E. (1995) "Transformation-Based Error-Driven Learning and Natural Language Processing: A Case Study in Part-of-Speech Tagging." Computational Linguistics, 21(4), 543-565. [PDF]
• Casacuberta, F. and Vidal, E. (2004) "Machine Translation with Inferred Stochastic Finite-State Transducers." Computational Linguistics, 30(2), 205-225. [PDF]
• Chomsky, N. (1962) Syntactic Structures (Second Printing). Janua Lingguarum nr. 4. Mouton & Co.
• Daciuk, J. (2002) "Comparison of Construction Algorithms for Minimal Acyclic, Deterministic, Finite-State Automata from Sets of Strings." In CIAA 2002. Lecture Notes in Computer Science no. 2608. Springer-Verlag; Berlin. 255-261. [PDF]
• Daciuk, J., Mihov, S., Watson, B.W., and Watson, R.E. (2000) "Incremental Construction of Acyclic Finite-State Automata." Computational Linguistics, 26(1), 3-16.
• Dalrymple, M. (2006) "How much can part-of-speech tagging help parsing?" Natural Language Engineering, to appear. [PDF]
• Damerau, F.J. (1964) "A Technique for Computer Detection and Correction of Spelling Errors." Communications of the ACM, 7(3), 171-176.
• Du, M.W. and Chang, S.C. (1992) "A model and a fast algorithm for multiple errors spelling correction." Acta Informtica, 29, 281-302.
• Garey, M.R., and Johnson, D.S. (1979) Computers and Intractability: A Guide to the Theory of NP-Completeness. W.H. Freeman; San Francisco, CA.
• Grana, J., Barcala, M., and Alonso, M.A. (2001) "Compilation Methods of Minimal Acyclic Finite-State Automata for Large Dictionaries." In CIAA 2001. Lecture Notes in Computer Science no. 2494. Springer-Verlag; Berlin. 135-148. [PDF]
• Hakkani-Tur, D.Z., Oflazer, K., and Tur, G. (2002) "Statistical Morphological Disambiguation for Agglutinative Languages." Computers and the Humanities, 36, 381-410. [PDF]
• Hazen, T.J., Hetherington, I.L., Shu, H., and Livesci, K. (2002) "Pronunciation Modeling using a Finite-State Transducer Representation." In Proceedings of the ICSA Tutorial and Workshop on Pronunciation Modeling and Lexicon Adaptation. [PDF]
• Hopcroft, J.E., Motwani, R., and Ullman, J.D. (2001) Introduction to Automata Theory, Languages, and Computation (Second Edition). Addison-Wesley. [Abbreviated above as HMU01]
• Hopcroft, J.E. and Ullman, J.D. (1979) Introduction to Automata Theory, Languages, and Computation. Addison-Wesley. [Abbreviated above as HU79]
• Kaplan, R.M. and Kay, M. (1994) "Regular Models of Phonological Rule Systems." Computational Linguistics, 20(3), 331-378. [PDF]
• Kari, L., Konstantinidis, S., Perron, S., Wozniak, G., and Xu, J. (2003) "Finite-state error.edit-systems and difference measures for languages and words." Technical report 2003-01, Department of Mathematics and Computing Science, Saint Mary's University, Canada. [PDF]
• Karttunen, L. (1998) "The Proper Treatment of Optimality Theory in Computational Phonology." Technical Report ROA-258-0498, Rutgers Optimality Archive. [PDF]
• Karttunen, L. (2000) "Applications of Finite-State Transducers in Natural Language Processing." In CIAA 2000. Lecture Notes in Computer Science no. 2088. Springer-Verlag; Berlin. 34-46. [PDF]
• Kiraz, G.A. (2000) "Multi-tiered nonlinear morphology using multitape finite automata: A case study on Syraic and Arabic." Computational Linguistics, 26(1), 77-105. [PDF]
• Kornai, A. (ed.) (1999) Extended Finite-State Models of Language. Cambridge University Press.
• Kruskal, J.B. (1984) "An Overview of Sequence Comparison." In D. Sankoff and J.B. Kruskal (eds.) Time Warps, String Edits, and Macromolecules: The Theory and Practice of Sequence Comparison. Addison-Wesley; Reading, MA. 1-44.
• Lucchesi, C.L. and Kowaltowski, T. (1993) "Applications of finite automata representing large vocabularies." Software - Practice and Experience, 23(1), 15-20. [PostScript]
• Mihov, S. and Maurel, D. (2000) "Direct Construction of Minimal Acyclic Subsequential Transducers." In CIAA 2000. Lecture Notes in Computer Science no. 2088. Springer-Verlag; Berlin. 217-229.
• Mihov, S. and Schulz, K.U.. (2004) "Fast Approximate Search in Large Dictionaries." Computational Linguistics, 30(4), 451-477. [PDF]
• Mohri, M. (1996) "On some applications of finite-state automata theory to natural language processing." Natural Language Engineering, 2(1), 61-80.
• Mohri, M. (2003) "Edit-Distance of Weighted Automata: General Definitions and Algorithms". International Journal of Foundations of Computer Science, 14(6), 957-982. [PDF]
• Mohri, M. (2004) "Weighted Finite-State Transducer Algorithms: An Overview." In Formal Languages and Applications. Studies in Fuzziness and Soft Computing no. 148. Physica-Verlag; Berlin. 551-564. [PDF]
• Mohri, M., Pereira, F., and Riley, M. (2000) "The Design Principles of a Weighted Finite-State Transducer Library." Theoretical Computer Science, 231, 17-32. [PDF]
• Mohri, M., Pereira, F., and Riley, M. (2002) "Weighted Finite-State Transducers in Speech Recognition." Computer Speech & Language, 16(1), 69-88. [PDF]
• Mohri, M., Riley, M., and Sproat, S. (1996) Algorithms for Speech Recognition and Language Processing. COLING'96 tutorial slides. [PDF]
• Myers, E.W. and Miller, W. (1989) "Approximate Matching of Regular Expressions." Bulletin of Mathematical Biology, 51, 5-37. [PDF]
• Nederhof, M.-J. (1996) "Introduction to Finite-State Techniques." Lecture notes. [PostScript/PDF]
• Nederhof, M.-J. (2000) "Practical Experiments with Regular Approximation of Context-Free Languages." Computational Linguistics, 26(1), 17-44. [PDF]
• Oflazer, K. (1996) "Error-Tolerant Finite-State Recognition with Applications to Morphological Analysis and Spelling Correction." Computational Linguistics, 22(1), 73-89. [PDF]
• Oflazer, K. (2003) "Dependency Parsing with an Extended Finite-Stte Approach." Computational Linguistics, 29(4), 515-544. [PDF]
• Oflazer, K. and Inkelas, S. (2003) "A Finite State Pronounciation Lexicon for Turkish." In EACL Workshop on FSMs in NLP. [PDF]
• Pereira, F., Riley, M., and Sproat, R. (1994) "Weighted Rational Transductions and their Application to Human Language Processing." In Proceedings: Worskhop on Human Language Technology. Association for Computational Linguistics; Somerset, NJ. 262-267. [PDF]
• Ritchie, G.D., Russell, G.J., Black, A.W., and Pullman, S.G. (1991) Computational Morphology: Practical Mechanisms for the English Lexicon. The MIT Press; Cambridge, MA.
• Roche, E. and Schabes, Y. (1995) "Deterministic Part-of-Speech Tagging with Finite-State Transducers." Computational Linguistics, 21(2), 227-253. [PDF]
• Roche, E. and Schabes, Y. (eds.) (1997) Finite-State Natural Language Processing. The MIT Press; Cambridge, MA.
• Rojc. M. and Kacic, Z. (2003) "Efficient Development of Lexical Language Resources and their Representations." International Journal of Speech Technology, 6, 259-275. [PDF]
• Savary, A. (2002) "Typographical Nearest-Neighbor Search in a Finite-State Lexicon and Its Application to Spelling Correction." In CIAA 2002. Lecture Notes in Computer Science no. 2494. Springer-Verlag; Berlin. 251-260. [PDF]
• Sproat, R.M. (1992) Morphology and Computation. The MIT Press; Cambridge, MA.
• Sproat, R. (1996) "Multilingual Text Analysis for Text-to-Speech Synthesis." In ECAI'96. John Wiley and Sons. 75-80. [PDF]
• Sproat, R. and Riley, M. (1996) "Compilation of Weighted Finite-State Transducers from Decision Trees." In ACL'96. 215-222. [PDF]
• Trancoso, I., Caseiro, D., Viana, C., Silva, F., and Mascarenhas, I. (2003) "Pronunciation modeling using finite state transducers." In ICPhS'2003. [PDF]
• Tzoukermann, E. and Radev, D.R. (1999) "Use of Weighted Finite State Transducers in Part of Speech Tagging." In Kornai, A. (ed.) (1999). 193-207. [PDF]
• Vilares, M., Otero, J., Barcala, F.M., and Dominguez, J. (2004) "Automatic Spelling Correction in Galician." In EsTAL 2004. Lecture Notes in Artificial Intelligence no. 3230. Springer-Verlag; Berlin. 45-57. [PDF]
• Vilares, M., Otero, J., and Grana, J. (2005) "Regional Versus Global Finite-State Error Repair." In CICLing 2005. Lecture Notes in Computer Science no. 3406. Springer-Verlag; Berlin. 120-131. [PDF]
• Vilares, M., Otero, J., and Vilares, J. (2006) "Robust Spelling Correction." In CIAA 2005. Lecture Notes in Computer Science no. 3406. Springer-Verlag; Berlin. 120-131. [PDF]
• Voutilainen, A. (1998) "Does tagging help parsing? A case study on finite state parsing." In Karttunen, L. (ed.) FSMNLP'98: International Workshop on Finite State Methods in Natural Language Processing. Association for Computational Linguistics; Somerset, NJ. 25-36. [PDF]
• Wagner, R.A. (1974) "Order-n Correction for Regular Languages." Communication of the ACM, 17(5), 265-268. [PDF]
• Wareham, H.T. (1999) Systematic Parameterized Complexity Analysis in Computational Phonology. PhD thesis, Department of Computer Science, University of Victoria.
• Wareham, H.T. (2001) "The Parameterized Complexity of Intersection and Composition Operations on Sets of Finite-State Automata." In CIAA 2000. Lecture Notes in Computer Science no. 2088. Springer-Verlag; Berlin. 302-310. [PostScript/ PDF]
• Watson, B.W. (1999) "Implementing and using finite automata toolkits." In Kornai, A. (ed.) (1999). 19-36.

Created: January 11, 2006
Last Modified: April 3, 2006