Computer Science 4750, Fall '14
Course Diary

Copyright 2014 by H.T. Wareham
All rights reserved

Week 1, Week 2, Week 3, Week 4, (In-class Exam #1 Notes),
Week 5, (Course Project and Proposal Notes),
Week 6, Week 7, Week 8, (In-class Exam #2 Notes),
Week 9, Week 10, Week 11, (Course Project Talk and Paper Notes), (In-class Exam #3 Notes),
Week 12, Week 13, Week 14, (end of diary)

Wednesday, September 3

Class canceled

Friday, September 5 (Lecture #1)
[Class Notes]

Went over course outline.
Introduction: What is Natural Language Processing (NLP)?
- NLP is the subfield of Artificial Intelligence (AI) concerned with the computations underlying the processing (recognition, generation, and acquisition) of natural human language (be it spoken, signed, or written).
  - NLP is distinguished from (though closely related to) the processing of artificial languages, e.g., computer languages, formal languages (regular, context-free, context-sensitive, etc).
- NLP emerged in the early 1950's with the first commercial computers; originally focused on machine translation, but subsequently broadened to include all natural-language related tasks (J&F, Section 1.6; Kay (2003); see also BKL, Section 1.5 and Afterword).
- Two flavours of NLP: weak and strong
  - The focus of strong NLP is on discovering and implementing human-level language abilities using approximately the same mechanisms as human beings when they communicate; as such, it is more closely allied with classical linguistics (and hence often goes by the name "computational linguistics").
  - The focus of weak NLP is on giving computers human-level language abilities by whatever means possible; as such, it is more closely allied with AI (and is often referred to by either "NLP" or more specific terms like "speech processing").
  - Weak NLP is nonetheless influenced by Strong NLP, and vice versa (to the extent that the mechanisms proposed in Weak NLP to get systems up and running help to revise and make more plausible the theories underlying Strong NLP).
  - In this course, we will look at both types of NLP, and distinguish them as necessary.
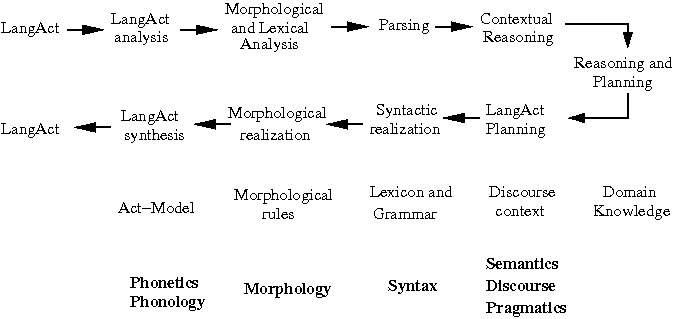
- General model of language processing (adapted from BKL, Figure 1.5):
  - "A LangAct" is an utterance in spoken or signed communication or a sentence in written communication.
  - The topmost left-to-right tier encodes language recognition and the right-to-left tier immediately below encodes language production.
  - The knowledge required to perform each step (all of which must be acquired by a human individual to use language) is the third tier, and the lowest is the area or areas of linguistics devoted to each type of knowledge.
  - Three language-related processes are thus encoded in this diagram: recognition and production (explicitly) and acquisition (implicitly).
- Whether one is modeling actual human language or implementing language abilities in machines, the mechanisms underlying each of language recognition, production, and acquisition must be able to both (1) handle actual human language inputs and outputs and (2) operate in a computationally efficient manner.
  - As we will see over the duration of this course, the need to satisfy both of these criteria is one of major explanations for how research has proceeded (and diverged) in Strong and Weak NLP.

Monday, September 8 (Lecture #2)
[Class Notes]

The Characteristics of Natural Language: Phonetics (J&M, Section 7)
- Phonetics is the study of the actual sounds produced in human languages (phones), both from the perspectives of how they are produced by the human vocal apparatus (articulatory phonetics) and how they are characterized as sound waves (acoustic phonetics).
  - Acoustic phonetics is particularly important in artificial speech analysis and synthesis.
- In many languages, the way words are written does not correspond to the way sounds are pronounced in those words, e.g., the sound corresponding to the letter "t" is pronounced differently in each of the words "toucan", "starfish", "kitten", and "butter" (see below). Hence, another way has to be used to describe the sounds people actually produce in speech.
- The most common way of representing phones is to use special sound-alphabets, e.g., International Phonetic Alphabet (IPA), ARPAbet (J&M, Table 7.1).
  - By convention, symbols denoting phones are written in square brackets, e.g., [b], [t].
  - Symbols in these alphabets may be modified by diacritics indicating more specific features of individual sounds, e.g., aspiration or palatalization, or the utterances in which these sounds occur, e.g., primary and secondary stress, utterance intonation.
- Another way of representing phones uses phonetic features based on how sounds are articulated in the human vocal tract, e.g.,
  - consonants:
    - voicing (voiced / unvoiced)
    - place of articulation (labial / dental / alveolar/ palatal / velar / glottal)
    - manner of articulation (stop / nasal / fricative / affricate (stop + fricative) / tap)
  - vowels:
    - height
    - "width" (front / back)
    - roundedness (rounded / unrounded)
- Sounds can vary depending on their context, due to constraints on the way articulators can move in the vocal tract when progressing between adjacent sounds (both within and between words) in an utterance.
  - Variation in pronouncing [t] (J&M, Table 7.9):
    - aspirated (in initial position), e.g., "toucan"
    - unaspirated (after [s]), e.g., "starfish"
    - glottal stop (after vowel and before [n], e.g., "kitten"
    - tap (between vowels), e.g., "butter"
  - word-final [t]/[d] palatalization (J&M, Table 7.10), e.g., "set your", "not yet", "did you"
  - Word-final [t]/[d] deletion (J&M, Table 7.10) e.g., "find him", "and we", "draft the"
- Variation in sounds may be probabilistic rather than deterministic, and can depend on a variety of factors, e.g., rate of speech, word frequency, speaker's state of mind / gender / class / geographical location (J&M, Section 7.3.3).
- As if all this wasn't bad enough, it is often very difficult to isolate individual sounds and words from acoustic speech signals

Wednesday, September 10 (Lecture #3)
[Class Notes]

Went over Question #1 on Assignment #1.

The Characteristics of Natural Language: Phonology (Bird (2010))

Phonology is the study of the systematic and allowable ways in which sounds are realized and can occur together in human languages.
Each language has its own set of semantically-indistinguishable sound-variants, e.g., [pat] and [p^hat] are the same word in English but different words in Hindi.
- The semantically-indistinguishable variants of a sound in a language are a phoneme in that language.
- By convention, symbols denoting phonemes are surrounded by right slashes, e.g., /b/, /t/.
- To continue the example above, [p] and [p^h] are part of phoneme /p/ in English but are part of separate phonemes /p/ and /p^h/ in Hindi.
- By definition, phonemes are both abstractions of phones and language-specific.

Variation in how phonemes are realized as phones is often systematic, e.g., formation of plurals in English:

mop	mops	[s]
pot	pots	[s]
pick	picks	[s]
mob	mobs	[z]
pod	pods	[z]
pig	pigs	[z]
pita	pitas	[z]

Note that the phonetic form of the plural-morpheme /s/ is a function of the last sound (and in particular, the voicing of the last sound) in the word being pluralized.

Such systematicity need involve non-adjacent sounds, e.g., vowel harmony in the formation of plurals in Turkish (Kenstowicz (1994), p. 25):

dal	dallar	``branch''
kol	kollar	``arm''
kul	kullar	``slave''
yel	yeller	``wind''
dis	disler	``tooth''
g"ul	g"uller	``race''

The form of the vowel in the plural-morpheme /lar/ is a function of the vowel in the word being pluralized.

It is tempting to think that such variation is encoded in the lexicon, such that each possible form of a word and its pronunciation are stored. However, such variation is often productive, suggesting that variation is is instead the result of processes that transform abstract underlying lexical forms to concrete surface pronounced forms.
- Unlimited concatenated morpheme vowel Harmony in Turkish (Sproat (1992), p. 44):
  In Turkish, complete utterances can consist of a single word in which the subject of the utterance is a root-morpheme (in this case, [c"op], "garbage") and all other (usually syntactic, in languages like English) relations are indicated by suffix-morphemes. As noted above, the vowels in the suffix morphemes are all subject to vowel harmony. Given the in principle unbounded number of possible word-utterance in Turkish, it is impossible to store them (let alone their versions as modified by vowel harmony) in a lexicon.
- Variation in English [r] according Cantonese phonology in Chinenglish (Demers and Farmer (1991), Exercise 3.10):
  - [r] deletion (before consonant or final sound in word), e.g., "tart", "party", "guitar", "bar", "sergeant"
  - [r] pronounced as [l] (before a vowel), e.g. "strawberry","brandy", "aspirin", "Listerine", "curry".
  These rules can also hold when a Cantonese speaker writes English text, e.g., "Phone Let Kloss about giving blood."

Friday, September 12 (Lecture #4)
[Class Notes]

The Characteristics of Natural Language: Phonology (Bird (2010))

It is tempting to think that such variation is encoded in the lexicon, such that each possible form of a word and its pronunciation are stored. However, such variation is often productive, suggesting that variation is is instead the result of processes that transform abstract underlying lexical forms to concrete surface pronounced forms. (Cont'd)

Modification of English loanwords in Japanese (Lovins (1973)):

dosutoru	``duster''
sutoroberri`	`strawberry''
kurippaa`	`clippers''
sutoraiki	``strike''
katsuretsu	``cutlet''
parusu	``pulse''
gurafu	``graph''

Japanese has a single phoneme /r/ for the liquid-phones [l] and [r]; moreover, it also allows only very restricted types of multi-consonant clusters. Hence, when words are borrowed from another language that violates these constraints, the words are changed by the modification to [r] or deletion of [l] and the insertion of vowels to break up invalid multi-consonant clusters.

There are also similar systematicities in allowable syllable structures as well as the placement of word stress, e.g., English penultimate ([ma + ri' + a]) vs. Polish antepenultimate ([ma' + ri + a]) word-stress. Such matters are the province of metrical phonology.
Each language has its own phonology, which consists of the phonemes of that language, constraints on allowable sequences of phonemes (phonotactics), and descriptions of how phonemes are instantiated as phones in particular contexts.
- As shown by the examples above, the systematicities within a language's phonology must be consistent with (but are by no means limited to those dictated solely by) vocal-tract articulator physics.
Courtesy of underlying phonological representations and processes, one is never sure if an observed phonetic representation corresponds directly to the underlying representation or is some process-mediated modification of that representation, e.g., we are never sure if an observed phone corresponds to an "identical" phoneme in the underlying representation. This introduces one type of ambiguity into natural language processing.

The Characteristics of Natural Language: Morphology (Trost (2003); Sproat (1992), Chapter 2)

Morphology is the study of the systematic and allowable ways in which symbol-string/meaning pieces are organized into words in human languages.
A symbol-string/meaning-piece is called a morpheme.
- Two broad classes of morphemes: roots and affixes.
- A root is a morpheme that can exist alone as word or is the meaning-core of a word, e.g., tree (noun), walk (verb), bright (adjective).
- An affix is a morpheme that cannot exist independently as a word, and only appears in language as part of word, e.g., -s (plural), -ed (past tense; 3rd person), -ness (nominalizer).
A word is essentially a root combined with zero or more affixes. Depending on the type of root, the affixes perform particular functions, e.g., affixes mark plurals in nouns and subject number and tense in verbs in English.
Morphemes are language-specific and are stored in a language's lexicon. The morphology of a language consists of a lexicon and a specification of how morphemes are combined to form words (morphotactics).
Morpheme order typically matters, e.g., uncommonly, commonunly*, unlycommon* (English)

There are a number of ways in which roots and affixes can be combined in human languages (Trost (2003), Sections 2.4.2 and 2.4.3):

Prefix: An affix attached to the front of the root, e.g.,, the negative marker un- for adjectives in English (uncommon, infeasible, immature).
Suffix: An affix attached to the back of the root, e.g.,, the plural marker -s for nouns in English (pots, pods, dishes).
Circumfix: A prefix-suffix pair that must both attach to the root, e.g.,, the past participle marker ge-/-t for verbs in German (gesagt "said", gelaufen "ran").

Infix: An affix inserted at a specific position in a root, e.g., the -um- verbalizer for nouns and adjectives in Bontoc (Philippines):

/fikas/	"strong"	/fumikas/	"to be strong"
/kilad/	"red"	/kumilad/	"to be red"
/fusl/	"enemy"	/fumusl/	"to be an enemy"

Template Infix: An affix consisting of a sequence of elements that are inserted at specific positions into a root (root-and-template morphology), e.g., active and passive markers -a-a- and -u-i- for the root ktb ("write") in Arabic:

katab	kutib	"to write"
kattab	kuttib	"cause to write"
ka:tab	ku:tib	"correspond"
taka:tab	tuku:tib	"write each other"

Reduplication: An affix consisting of a whole or partial copy of the root that can be prefix, infix, or suffix to the root, e.g., formation of the habitual-repetitive in Javanese:

/adus/	"take a bath"	/odasadus/
/bali/	"return"	/bolabali/
/bozen/	"tired of"	/bozanbozen/
/dolan/	"recreate"	/dolandolen/

(MEANINGFUL WHISPER: Do you see anything that makes reduplication qualitatively different from all other phonological and morphological processes that we have considered here? (Hint: a^n b^n => ww))

As with phonological variation, there are several lines of evidence which suggest that morphological variation is not purely stored in the lexicon but rather the result of processes operating on underlying forms:
- Productive morphological combination simulating complete utterances in words, e.g., Turkish example above.
- Morphology operating over new words in a language, e.g., blicket -> blickets, television -> televise -> televised / televising, barbacoa (Spanish) -> barbecue (English) -> barbecues.
As if all this didn't make things difficult enough, different morphemes need not have different surface forms, e.g, variants of "book"
Courtesy of phonological transformations operating both within and between morphemes and the non-uniqueness of surface forms noted above, one is never sure if an observed surface representation corresponds directly to the underlying representation or is a modification of that representation, e.g., is [blints] the plural of "blint" or does it refer to a traditional Jewish cheese-stuffed pancake? This introduces another type of ambiguity into natural language processing.

Week 3 [Class Notes]

Monday, September 15 (Lecture #5)
[Class Notes]

The Characteristics of Natural Language: Syntax (BKL, Section 8; J&M, Chapter 12; Kaplan (2003))

Syntax is the study of the systematic and allowable ways in which words are organized into utterances (spoken) and sentences (written) in human languages.
Two fundamental facts of natural language syntax (J&M, pp. 385-386):
- constituency: a group of one or more (most often, adjacent) words may behave as a single unit called a constituent, e.g., "fox", "dog", "jumped", "the quick brown fox", "the lazy dog", and "jumped over the lazy dog" are constituents in the utterance "the quick brown fox jumped over the lazy dog".
- grammatical relations: constituents relate in systematic manners to other constituents in a utterance, e.g. "the quick brown fox" and "the lazy dog" are the subject and object, respectively, in the utterance "The quick brown fox jumped over the lazy dog".
Constituents typically have associated grammatical classes whose members may have different structures but perform equivalent grammatical functions, e.g., noun phrase, determiner, verb phrase.
- Analogous to the manner in which phonemes are built up from phones, constituents are grouped into grammatical classes based on whether or not the members can be substituted for each other to create grammatical utterances, e.g., Given that "the quick brown fox", "an airplane", "John", "Alice from the second house down the lane", and "the man who Liberty Valence" can all be substituted for X in the utterance "X jumped over the lazy dog" to create grammatical (if somewhat puzzling) utterances, all are examples of a common constituent class (in this case, noun phrases).
- There are typically multiple hierarchical levels of constituents in an utterance, e.g.,
  
  "[[the [quick [brown [fox]]]] [jumped over [the [lazy [dog]]]]]".

Grammatical relations can express what constituents can co-occur in an utterance (subcategorization) or the semantic relationships between constituents (dependency).

Some languages encode grammatical relations primarily by word order, e.g., "John visited Mary" (English); others primarily use morphology, e.g., "John-ga Mary-o tazune-ta", "Mary-o John-ga tazune-ta" (Japanese) (Kaplan (2003), p. 71).

Even in languages that primarily use word order and have equivalent grammatical classes, orders of grammatical classes may differ across languages, e.g, each of the six possible orderings of subject, object, and verb in basic transitive-verb utterances occur in at least one human language. though the frequencies of these orders vary greatly (Tomlin (1986), p. 22):

SOV	"She him loves."	45%	Pashto, Latin, Japanese, Afrikaans
SVO	"She loves him."	42%	English, Hausa, Mandarin, Russian
VSO	"Loves she him."	9%	Hebrew, Irish, Zapotec, Tuareg
VOS	"Loves him she."	3%	Malagasy, Baure
OVS	"Loves him she."	1%	Apalai, Hixkaryana
OSV	"Him she loves."	< 1%	Warao

Grammatical relations can hold over arbitrary distances in a utterances, e.g., "The man who knew the solder that killed the sailor who sailed as first mate on the S.S. Warsaw and visited my ex-sister-in-law Louise's best friend in Paris last month died." (garden-path utterances)
Grammatical relations may even be recursively embedded, e.g., "The cat the dog the rat the elephant admired bit chased likes tuna fish." (J&M, p. 536)
(MEANINGFUL WHISPER: Is such embedding of constituents qualitatively different from other syntactic patterns considered above? (Hint: a^n b^n))

Syntax is language-specific. Building on a language's morphology, the syntax is a specification called a grammar of how words are combined to form utterances in that language.
- Languages such Japanese and Turkish (see above) that use word-internal morphology to a greater degree than word order to encode grammatical relations and dependencies are said to have a morphosyntax.
Analogous to phonological and morphological variation, the fact that syntax operates productively to generate a potentially infinite number of utterances over a finite lexicon suggests that syntactic patterns are not purely stored in the grammar but are rather the result of grammatical processes operating on underlying forms.
As if all this didn't make things difficult enough, utterances expressing very different meanings need not have different surface forms, e.g,
Hence, ambiguity inherent in grammars and lexicons adds yet another type of ambiguity into natural language processing (BKL, pp. 317-318).

Wednesday, September 17 (Lecture #6)
[Class Notes]

The Characteristics of Natural Language: Semantics, Discourse, and Pragmatics (Lappin (2003); Leech and Weisser (2003); Ramsay (2003))
- Semantics is the study of the manner in which meaning is associated with utterances in human language; discourse and pragmatics focus, respectively, on how meaning is maintained and modified over the course of multi-person dialogues and how these people chose different individual-utterance and dialogue styles to communicate effectively.
- Meaning seems to be very closely related to syntactic structure in individual utterances; however, the meaning of an utterance can vary dramatically depending on the spatio-temporal nature of the discourse and the goals of the communicators, e.g., "It's cold outside." (statement of fact spoken in Hawaii; statement of fact spoken on the International Space Station; implicit order to close window).
- Various mechanisms are used to maintain and direct focus within an ongoing discourse (Ramsay (2003), Section 6.4):
  - Different syntactic variants with subtly different meanings, e.g., "Ralph stole my bike" vs "My bike was stolen by Ralph".
  - Different utterance intonation-emphasis, e.g., "I didn't steal your bike" vs "I didn't steal your BIKE" vs "I didn't steal YOUR bike" vs "I didn't STEAL your bike" (see also Travis Bickle in TAXI DRIVER)
  - Syntactic variants which presuppose a particular premise, e.g., "How long have you been beating your wife?"
  - Syntactic variants which imply something by not explicitly mentioning it, e.g., "Some people left the party at midnight" (-> and some of them didn't), "I believe that she loves me" (-> but I'm not sure that she does).
- Another mechanism for structuring discourse is to use references (anaphora) to previously discussed entities (Mitkov (2003a)).
  - There are many kinds of anaphora (Mitkov (2003a), Section 14.1.2):
    - Pronominal anaphora, e.g., "A knee jerked between Ralph's legs and he fell sideways busying himself with his pain as the fight rolled over him."
    - Adverb anaphora, e.g., "We shall go to McDonald's and meet you there."
    - Zero anaphora, e.g., "Amy looked at her test score but was disappointed with the results."
    - Nominal anaphora (direct), e.g., "Keane plays football for Manchester United. Irishman Keane has three years left in his current contract."
    - Nominal anaphora (indirect), e.g., "Although the store had just opened, the food hall was full and customers were lined up at the cash registers."
  - Though a convenient conversational shorthand, anaphora can be (if not carefully used) ambiguous, e.g.,
- As demonstrated above, utterance meaning depends not only the individual utterances, but on the context in which those utterance occur (including knowledge of both the past utterances in a dialogue and the possibly unknown and dynamic goals and knowledge of all participants in the discourse), which adds yet another layer of ambiguity into natural language processing ...
It seems then that natural language, by virtue of its structure and use, encodes both a lot of ambiguity and variation, as well as a wide variety of grammatical structures at all levels.
- The amount and type of ambiguity and variation that must be accommodated by mechanisms in a natural language processing system varies depending on the goals of the system:
  - If the system must operate fluently on unstructured input relative to unstructured conversational domains, every form of ambiguity and variation mentioned above must be dealt with.
  - If the system must operate only relative to a restricted set of conversational forms and topics, e.g., a telephone-accessed airline flight status information system (especially one that asks questions in a structured manner to control user inputs), the amount of ambiguity (and to a degree variation) at the discourse, syntax, and morphological levels can be dramatically restricted.
  - If the system in addition operates relative to a single known user relative to which that system can be trained, e.g., an on-line personal assistant, the amount of ambiguity at the phonological and phonetic levels (as well as variation at all levels) can also be dramatically restricted.
- The types of grammatical structures that must be accommodated by mechanisms in a natural language processing system varies depending on the goals of the system:
  - If the goal is to operate fluently within an economically dominant language, e.g., English, Mandarin, Arabic, Hindi, then one can focus on mechanisms tailored specifically to the types of structures in that language (though to achieve fluent communication, extra attention will have to be paid to fine-grained structure within that language).
  - If the goal is to help preserve languages that have less economic dominance or are rapidly dying out ("rescue linguistics"), e.g., Danish, Manx, Warao, Apalai, then one requires mechanisms that can handle many types of structure (though less attention may be required to fine-grained structure within that language, especially in the case of time-constrained rescue linguistics).

Friday, September 19 (Lecture #7)
[Class Notes]

In any case, there is a final set of computational characteristics of natural language that must be either accommodated (in the case by strong NLP systems) or circumvented by clever means (in the case of weak NLP systems).
The Characteristics of Natural Language: Natural Language Operation and Acquisition
- Human beings (both adults and children) use language effectively with the aid of finite and ultimately limited computational devices, e.g., our brains.
- Utterances are generated and comprehended relatively quickly in most everyday situations, cf., bad telephone connections active construction sites.
- Generation and performance acquisition degrades more or less gracefully with the increasing complexity and length of utterances.
- Given exposure to a human language, any child can acquire the phonological, morphological, and semantic (if not total lexical) knowledge of that language within four to seven years.
  - This exposure does not need to be simplified, cf., Motherese.
  - This exposure does not need to be comprehensive or exhaustive, with many examples of each possible phenomena in the language.
  - Individual utterances in this exposure need not be either grammatical or have their grammaticality-status stated.
  - Produced utterances by the child need not be assessed for grammaticality or corrected.
- Given exposure to any human language, any human being can acquire that language, and children under the age of 10 years are superbly good at this. In addition:
  - If children are exposed to two distinct language simultaneously, they will acquire both languages, i.e., they will become bilingual.
  - If children are exposed to a pidgin created by combining elements of two or more languages, they will regularize the unsystematic parts of the pidgin to create a proper hybrid language (creole).
Given all these characteristics and their explicit and implied constraints on what an NLP system must do, what then are appropriate computational mechanisms for implementing NLP systems? It is appropriate to consider first what linguists, the folk who have been studying natural language for the longest time, have to say on this matter.
NLP Mechanisms: The View from Linguistics
- Given that linguistic signals are expressed as temporal (acoustic and signed speech) and spatial (written sequences) sequences of elements, there must be a way of representing such sequences.
  - Sequence elements can be atomic (e.g., symbols) or have their own internal structure (e.g., feature matrices, form-meaning bundles (morphemes)); for simplicity, assume for now that elements are symbols.
  - There are at least two types of such sequences representing underlying and surface forms.
  - Where necessary, hierarchical levels of structure such as syntactic parse trees can be encoded as sequences by using appropriate interpolated and nested brackets, e.g., "[[the quick brown fox] [[jumped over] [the lazy brown dog]]]"
- The existence of lexicons implies mechanisms for representing sets of element-sequences, as well as accessing and modifying the members of those sets.
- The various processes operating between underlying and surface forms presuppose mechanisms implementing those processes.
  - Two broad classes of linguistic process-systems:
    - Rule-based: Individual processes are rules that specify transformations of one form to another form, e.g., add voice to the noun-final plural morpheme /s/ if the last sound in the noun is voiced.
    - Constraint-based: Individual processes are constraints that specify valid structures in surface and underlying forms, e.g., the voicing of the surface form of the noun-final plural morpheme must match the voicing of the final sound in the noun being pluralized.
  - In rule-based systems, rules are applied in a specified order to transform an underlying form to its associated surface form for utterance production, and in reverse fashion to transform a surface form to its associated underlying form(s) for utterance comprehension (ambiguity creating the possibility of multiple such associated forms).
  - In constraint-based systems, constraints are applied simultaneously to an underlying (surface) form to create associated composite surface-underlying form(s) in the case of utterance generation (comprehension).
- In the simplest cases, we may assume that all processes operate in a deterministic fashion; however, given the complexity of proposed processes and how they may interact, it may be useful as an intermediate stage in analyzing linguistic complexity to allow mechanisms that operate probabilistically, e.g., rules that have a specified probability of application.
  - This is analogous to the use of statistical mechanics to summarize and analyze the overall motion of large groups of particles in physics.
  - Such mechanisms may be analysis end-points in themselves if it turns out that either the interaction of deterministic linguistic processes is too complex to untangle or there are probabilistic processes underlying natural language processing in humans.

Week 4 [Class Notes]

Monday, September 22 (Lecture #8)
[Nederhof (1996); Class Notes]

NLP Mechanisms: Finite-state grammars, automata, and transducers
- Regular (finite-state) Grammars (HU79, Section 9.1; J&M, Section 2.2; Martin-Vide (2003), Section 8.2.4)
  - Originated in the Linguistics community; proposed by Chomsky in the 1950s as the lowest level of the Chomsky Hierarchy of grammars (Regular / Context-Free (Phrase Structure) / Context-Sensitive / Unrestricted).
  - Basic terminology: (production) rule, terminal, non-terminal, rule application, termination.
    - Rules are restricted such that left-hand side is a single non-terminal and the right-hand side is of length at least one and consists of zero or more terminal followed by at most one non-terminal.
    - Without loss of generality, we will focus on regular grammars with at most one terminal on the right-hand side.
  - Operation: generation / recognition of strings
  - Example: A regular grammar for the set of all strings over the alphabet {a,b} that consist of one or more concatenated copies of ab.
  - Example: A regular grammar for the set of all strings over the alphabet {a,b} that start with an a and end with a b (Version I).
  - Example: A regular grammar for the set of all strings over the alphabet {a,b} that start with an a and end with a b (Version II).
  - Example: A regular grammar for the set of all strings over the alphabet {a,b} that start with an a and end with a b (Version III).
  - Example: A regular grammar implementing the constraint that the voicing of the surface form of the noun-final plural morpheme must match the voicing of the final sound in the noun being pluralized.

Wednesday, September 24

Instructor sick; class canceled

Thursday, September 25

In-class Exam #1 Notes
I've finished making up the first in-class exam. The exam will be closed-book. It will be 50 minutes long and has a total of 50 marks (this is not coincidental; I have tried to make the number of marks for a question approximately equivalent to the number of minutes it should take you to do it). The exam will cover material in all course lectures up to and including Lecture # 9. There will be three questions:
- Characteristics of natural language (3 parts / 22 marks total)
- Basic Python programming (2 parts / 20 marks total)
- Mechanisms for implementing natural language processing (3 parts / 8 marks)
I hope the above helps, and I wish you all the best of luck with this exam.

Friday, September 26 (Lecture #9)
[Nederhof (1996); Class Notes (Figure PDF)]

NLP Mechanisms: Finite-state grammars, automata, and transducers (Cont'd)
- Finite-state automata (FSA) (Martin-Vide (2003), Section 8.3.1; Nederhof (1996); Roche and Schabes (1997a), Section 1.2)
  - Originated in the Engineering community; inspired by the discrete finite neuron model proposed by McCullough and Pitts in 1943.
  - Basic Terminology: (start / finish) state. (symbol-labeled) transition, configuration, acceptance.
  - Operation: generation / recognition of strings
    - Generation builds a string from left to right, adding symbols to the right-hand end of the string as one progresses along a transition-path from the start state to a final state.
    - Recognition steps through a string from left to right, deleting symbols from the left-hand end of the string as one progresses along a transition-path from the start state to a final state.
    - Note that one need only keep track of one FSA-state during both operations described above, namely, the last state visited.
  - Types of FSA:
    - Deterministic (DFA): At each state and for each symbol in the alphabet, there is at most one transition from that state labeled with that symbol.
    - Non-Deterministic (NFA): At each state, there may be more than one transition from that state labeled with a particular symbol and/or there may be transitions labeled with special symbol epsilon.
      - Revised notion of string acceptance: see if there is any path through the NFA that accepts the input string.
    - DFA can recognize strings in time linear in the length of the input string, but may not be compact; NFA are compact but may require time exponential in the length of a string to recognize that string (need to follow all possible computational paths to check string acceptance).
  - Example #1 (see figure): A DFA for the set of all strings over the alphabet {a,b} that consist of one or more concatenated copies of ab.
  - Example #2 (see figure): An NFA for the set of all strings over the alphabet {a,b} that start with an a and end with a b (uses multiple same-label outward transitions).
  - Example #3 (see figure): An NFA for the set of all strings over the alphabet {a,b} that start with an a and end with a b (uses epsilon-transitions).
  - Example #4 (see figure): A DFA for the set of all strings over the alphabet {a,b} that start with an a and end with a b.
  - Example #5 (see figure): A DFA implementing the constraint that the voicing of the surface form of the noun-final plural morpheme must match the voicing of the final sound in the noun being pluralized.
  - Oddly enough, deterministic and non-deterministic FSA are equivalent in recognition power, i.e., there is a DFA for a particular set of strings iff there is an NFA for that set of strings.
    - Determinization algorithm (HMU01, Section 2.5.5)
      - Creates DFA from a |Q|-state NFA in O(|Q|^3 * 2^{|Q|}) time and O(2^{|Q|}) space. add up).
      - DFA produced by this algorithm can be exponentially larger (in terms of the number of states) than the input NFA (HMU01, Section 2.3.6).
    - Minimization algorithm (HU79, pp. 67-71)
      - Creates minimal DFA from a |Q|-state DFA operating over alphabet Sigma in O(|Sigma||Q|^2) time; this is, however, potentially still exponential time if the input DFA was created by the determinization algorithm above.
      - This algorithm cannot be bused to minimize NFA; indeed, there does not appear to be a subexponential time and space algorithm for minimizing NFA (HMU01, p. 163).
- Regular grammars and finite-state automata are equivalent in recognition power, i.e, there is a DFA for a particular set of strings iff there is a regular grammar for that set of strings (HMU01, Section 4.3.1).
  - There is actually another notation, regular expressions, which is also equivalent in recognition power to regular grammars and finite-state automata.
  - A regular expression is essentially a way of expressing the left-to-right structure of each string in a set of strings in a linear fashion.
  - Example: A regular expression for the set of all strings over the alphabet {a,b} that consist of one or more concatenated copies of ab is (ab)^*.
  - Example: A regular expression for the set of all strings over the alphabet {a,b} that start with an a and end with a b is a(a|b)^*b.
- Given the focus on defining and combining groups of simple to complex processes at the level of phonology and morphology and the structure of the lexicon in morphology, NLP applications use finite-state automata rather than regular grammars.
  - Regular expressions are frequently used to describe simple FSA, especially when these FSA are used as inputs to software packages, e.g., xFST (Beesley and Karttunen (2003)); however, they are not suited to describing the complex composite FSA created by combining multiple FSA in NLP applications.
- Regular grammars and finite-state automata encode sets of strings, and are hence good for encoding simple lexicons or simple (one-level) constraint-processes; how do we encode the relations or functions between pairs of strings in rule-processes functions encoded in rule- processes or complex (two-level) constraint-processes?

Week 5 [Class Notes]

Monday, September 29

In-class Exam #1

Wednesday, October 1 (Lecture #10)
[Nederhof (1996); Class Notes (Figure PDF)]

NLP Mechanisms: Finite-state grammars, automata, and transducers (Cont'd)
- Finite-state transducers (FST) (J&M, Section 3.4, Mohri (1997); Roche and Schabes (1997a), Section 1.3)
  - Generalization of FSA in which each transition is labeled with a symbol-pair (either or both of which may be the special symbol epsilon).
    - The first symbol in each pair is called the lower symbol and the second is called the upper symbol.
    - The alphabet of all lower-symbols in an FST need not have a non-empty intersection with the alphabet of all upper-symbols in an FST.
  - Operation: generation / recognition of string-pairs, reconstruction of upper (lower) string associated with given lower (upper) string.
    - Generation of a string-pair builds that pair from left to right, adding symbol-pairs to the right-hand end of the string-pair as one progresses along a transition-path from the start state to a final state.
    - Recognition of a string-pair proceeds by stepping through that pair from left to right, deleting symbol-pairs from the left-hand end of the string-pair as one progresses along a transition-path from the start state to a final state.
    - Reconstruction of a string-pair associated with a given string builds the missing string of the pair from left to right, adding missing-string symbols to the right-hand end of the missing string as one progresses along a transition-path from the start state to a final state in accordance with the given string.
      - As the given string may be either the lower or upper string, there are two types of string-pair reconstructions.
      - Each reconstructed string-pair corresponds to a particular path through the FST guided by the given string.
      - Depending on the structure of the FST, there may be more than one path through the FST consistent with the given string, and hence more than one string-pair reconstruction.
    - Note that one need only keep track of one FST-state during all operations described above, namely, the last state visited.
  - Unlike FSA, there are many types of FST and many types of determinism; for each such type, there are different determinization and minimization algorithms (Kaplan and Kay (1994); Mohri (1997), 2004; Roche and Schabes (1997a), Section 1.3).
    - The most basic type of deterministic is an l/u-deterministic FST, such that for each state q in the FST and each lower/upper symbol-pair x/y, there is at most one transition outwards from q with label x/y.
  - Example #1 (see figure): An FST for transforming between the set of all strings over the alphabet {a,b} that consist of l, l >= 0, concatenated copies of ab and the set of all strings over the alphabet {c,d} that consist of l, l >= 0, concatenated copies of cd.
  - Example #2 (see figure): An FST for transforming between the set of all strings over the alphabet {a,b} that consist of l, l >= 0, concatenated copies of ab and the set of all strings over the alphabet {a,b} that consist of l, l >= 0, concatenated copies of aba.
  - Example #3 (see figure): An FST implementing the rule that voice be added to the noun-final plural morpheme /s/ if the last sound in the noun is voiced.
  - Example #4: An FST implementing the rule that (1) voice be added to the noun-final plural morpheme /s/ if the last sound in the noun is voiced and (2) an extra vowel be added before the plural morpheme if the last sound in the noun is [sh] or [zh], e.g., dishes, buzzes.
- Probabilistic versions of all three finite-state mechanisms described above can be defined:
  - Probabilistic finite-state grammars: Add probabilities to each rule such that for each nonterminal X, the sum of the probabilities of all rules with X as the left-hand side is 1.0.
  - Probabilistic finite-state automata and transducers: Add probabilities to each transition such that for each state Q, the sum of the probabilities of all transitions going outwards from Q is 1.0.
  Probabilistic finite-state automata and transducers are special cases of weighted finite-state automata and transducers (Mohri (2004)).
Finite-state mechanisms can handle many basic linguistic phenomena like concatenation, contiguous long-distance dependency, and finite numbers of long-distance dependencies, e.g., local phonological modification, vowel harmony, Turkish morphology, garden-path utterances.
However, it can be formally proved (see J&M, Section 16.2.2 and references) that finite-state mechanisms cannot handle more complex phenomena like unbounded numbers of long-distance dependencies, e.g., phonological reduplication, recursively embedded-relation utterances.
We need something more powerful -- but what?

Friday, October 3 (Lecture #11)
[Class Notes (Figure PDF)]

NLP Mechanisms: Context-free grammars and pushdown automata (BKL, Section 8.3; HU79, Chapter 5; Martin-Vide (2003), Sections 8.2.1 and 8.3.2)
- Context-free grammars (CFG) (BKL, Section 8.3; Martin-Vide (2003), Section 8.2.1)
  - Originated in the Linguistics community; proposed by Chomsky in the 1950s as the second level of the Chomsky Hierarchy of grammars (Regular / Context-Free (Phrase Structure) / Context-Sensitive / Unrestricted).
  - Basic terminology: (production) rule, terminal (plus special symbol epsilon), non-terminal, rule application, termination.
    - Rules are restricted such that left-hand side is a single non-terminal and the right-hand side s of length at least one consisting of any sequence of terminals and/or non-terminals.
  - Operation: generation / recognition of strings
    - Both generation and recognition create parse trees such that each internal node and its immediate children in the tree corresponds to the application of a rule in a CFG.
    - Note that regular grammars also produce parse trees, though of a much more restricted type, i.e., right-linear.
  - Example #1 (see figure): A CFG for the set of all strings over the alphabet {a,b} that consist of n >= 1 a's followed by n b's.
  - Example #2 (see figure): A CFG for a finite-size subset of all utterances:
  - Example #3 (see figure): A CFG for an infinite-size subset of all garden-path utterances, e.g., "The man who knew the solder that killed the sailor who sailed as first mate on the S.S. Warsaw and visited my ex-sister-in-law Louise's best friend in Paris last month died.":
  - Example #4 (see figure): A CFG for an infinite-size subset of the set of all recursively-embedded utterances, e.g., "The cat the dog the rat the elephant admired bit chased likes tuna fish." (J&M, p. 536)
  - Example #5 (see figure): A CFG for an infinite-size subset of the set of all utterances, e.g. "the dog saw a man in the park" (BKL, pp. 298-299).
    Unlike the other sample grammars above, this grammar is structurally ambiguous because there may be more than one parse for certain utterances involving prepositional phrases (Pp) as it is not obvious which noun phrase (Np) a Pp is attached to, e.g., in "the dog saw the man in the park", is the dog or the man in the park?
  - Note that the parse trees encode grammatical relations between entities in the utterances, and that these relations have associated semantics; hence, one can use parse trees as encodings of basic utterance meaning!
    - As shown in Example #5 above, parse trees via structural ambiguity can nicely encode semantic ambiguity.
- A pushdown automaton (PDA) is essentially an NFA that is augmented with a stack-memory (HU79, Sections 5.1 and 5.2).
- CFG and PDA are equivalent in recognition power, i.e, there is a CFG for a particular set of strings iff there is a PDA for that set of strings (HU79, Section 5.3).
- Given the traditional focus on rule-based syntactic descriptions, NLP applications use CFG rather than PDA.
- Probabilistic versions of CFG and PDA can be defined in a manner analogous to that for probabilistic regular grammars and FSA (BKL, Section 8.6; J&M, Section 14,1).
Context-free mechanisms can handle many more complex linguistic phenomena like unbounded numbers of recursively-embedded long-distance dependencies; however, there are still phenomena that require more power, e.g., phonological reduplication.
Though there is wide-spread consensus in the linguistics community that natural language cannot be fully captured by context-free mechanisms (Gazdar and Pullum (1985); Martin-Vide (2003), p. 169), almost all NLP systems use context-free or finite-state mechanisms.
- Given the relative computational simplicity and efficiency of finite-state mechanisms and good known techniques for approximating context-free grammars with finite-state mechanisms (see Nederhof (2000) and references), many NLP systems exclusively use finite-state mechanisms.
Given the above, in the remainder of this course, we will consider NLP implementations relative to finite-state and context-free mechanisms, starting first with deterministic mechanisms and then progressing to probabilistic versions.

Week 6 [Class Notes]

Monday, October 6

Course Project and Proposal Notes
Over the next several weeks, you should choose the topic of your course project. This project can take the form of a literature survey on an NLP topic of interest to you or a software system implementing a particular NLP task. Each course project *** MUST *** be approved by the course instructor; please do this by chatting with your course instructor by October 31st. Course projects that are not approved prior to the submission of the associated project proposal (see below) will receive a mark of zero.,
Once a course project is approved, you must write and submit a project proposal due at noon on Monday, November 3, and worth 5 course marks. This proposal should be about a page long and consist of a 3-paragraph proposal text (3.5 marks total) (with the first paragraph motivating why your topic is of interest (1 mark), the second summarizing previous work on this topic (1.5 marks), and the third summarizing the focus of your survey or the approach you will use in constructing your software system (1 mark)) followed by at least five full-information literature references particular to the topic of your project which must each be cited at least once in your proposal text (1.5 marks total) (0.3 marks per reference up to 5 references).
Once the project proposal is submitted, you have until noon on Wednesday, December 3, to do your project. Ideally, the submitted project should be the same as that described in your project proposal. However, it being an imperfect world, if any difficulties do arise, chat with your course instructor as soon as possible so appropriate action, e.g., revision of stated goals and/or scope of project, can be taken.
Each project will also have an associated short in-class presentation scheduled in late November and early December. Details of talk format and scheduling will be posted in early November after project proposals are submitted.
Here's to each of you choosing and carrying out a fun course project!

Monday, October 6 (Lecture #12)
[Nederhof (1996); Class Notes (Figure PDF)]

When assessing the running time and space requirements of FSA and FST operation algorithms, it is often assumed that (1) alphabet size is fixed and can be ignored, and (2) the computational effort required to process states is primary and the effort required to process transitions can be ignored.
These assumptions are problematic in NLP applications, as (1) individual processes can often be encoded as FSA or FST with few states that operate over large alphabets (and hence potentially have many transitions) and (2) in the case of state-pair-based constructions like that for intersection below, consideration of transitions makes detailed worst-case resource bounds much worse than they initially appear.
Hence, to better evaluate the actual time-space requirements of FSA and FST operations, we will below employ more complex time and space complexity expressions that take alphabet size and transition-processing resource requirements into account.
Working with Finite-state Automata
- Implementing basic operations
  - Checking acceptance of a string s by an FSA F:
    - Adapt the classic depth-first search algorithm to follow a state-sequence (if one exists) by which s is accepted by F.
      Note implicit handling of epsilon-transitions in this algorithm.
    - If F is a DFA, the above can be replaced by a much simpler iterative non-recursive algorithm; however, the algorithm above works for both DFA and NFA. and is safer to use if you're not sure what kind of FSA you will be working with.
    - If F is a DFA, the algorithm above runs in O(|s|) time and space. If F is an NFA, the algorithm runs in O((2|Q|)^|s|) time and O(|Q||s|) space, where |Q| is the number of states in F.
  - Focus on FSA combination operations that are closed, i.e., operations on one or more FSA that yield another FSA.
  - Let F1 and F2 be two FSA which recognize the sets of strings S1 and S2, respectively, and assume without loss of generality that all strings in S1 and S2 are over a common alphabet Sigma. Let us consider several operations that combine F1 and F2 to create an FSA FR.
  - Concatenation of F1 and F2 (HMU01, p. 133)
    - FR recognizes all strings xy such that x is in S1 and y is in S2.
    - The simplest way to create create FR is as follows:
      - Add a copy each of F1 and F2 to FR.
      - Make the start state qs2 of F2 a regular state.
      - For each final state qf1 of F1, make qf1 a regular state and connect it by an epsilon transition to qs2.
      As the FR so created is an NFA, determinization may be a good idea.
    - Note that the start state of FR is qs1 and the final states of FR are the final states of F2.
    - Example #1 (see figure): A FSA that recognizes the concatenation of the sets of strings over the alphabet {a,b} that contain at least one a and contain at least one b, respectively.
    - If F1 and F2 have |Q1| and |Q2| states, respectively, FR is a (|Q1| + |Q2| - 1)-state FSA that is created in O(|Sigma|(|Q1| + |Q2|)) time and space.
  - Union of F1 and F2 (HMU01, p. 132)
    - FR recognizes all strings x such that x is in S1 and/or x is in S2.
    - The simplest way to create FR is as follows:
      - Add copies of F1 and F2 to FR.
      - Add new start and final states qs and qf to FR.
      - Connect qs to qs1 and qs2 by epsilon transitions and make qs1 and qs2 regular states.
      - For each final state qfi in F1 and F2, connect qfi to qf by an epsilon transition and make qfi a regular state.
      As the FR so created is an NFA, determinization may be a good idea.
    - Example #2 (see figure): A FSA that recognizes the union of the sets of strings over the alphabet {a,b} that contain at least one a and contain at least one b, respectively.
    - If F1 and F2 have |Q1| and |Q2| states, respectively, FR is an (|Q1| + |Q2| + 2)-state FSA that is created in O(|Sigma|(|Q1| + |Q2|)) time and space.
  - Intersection of F1 and F2 (HMU01, pp. 134-137; Kaplan and Kay (1996))
    - FR recognizes all strings x such that x is in S1 and x is in S2.
    - Create FR as follows:
      - For each state q1 in F1 and and q2 in F2, add state (q1,q2) to FR.
      - Add the following transitions to FR:
        
        ((q1,q2),s,(q3,q4)) such that there are transitions (q1,a,q3) in F1 and (q2,a,q4) in F2;
        ((q1,q2),epsilon,(q1,q4)) such that there are transitions (q1,a,q3) in F1 and (q2,epsilon,q4) in F2; and
        ((q1,q2),epsilon,(q3,q2)) such that there are transitions (q1,epsilon,q3) in F1 and (q2,s,q4) in F2.
      As the FR so created may be an NFA, determinization may be a good idea.
    - Note that the start state of FR is (qs1,qs2) and the final states of FR are all states (q1,q2) such that q1 is a final state in F1 and q2 is a final state in F2.
    - The FSA FR above essentially simulates the operation of F1 and F2 in parallel, and accepts only those strings that are accepted by both F1 and F2.
    - Example #3 (see figure): A FSA that recognizes the intersection of the sets of strings over the alphabet {a,b} that contain at least one a and contain at least one b, respectively.
    - If F1 and F2 have |Q1| and |Q2| states, respectively, FR is a |Q1||Q2|-state FSA that is created in O(|Sigma|(|q1||Q2|)^2) time and space.
  - Various other operations on FSA are known and defined, e.g., complementation, repetition, reversal, subtraction, and all run in low-order polynomial time and space (HMU01, Section 4.2).

Wednesday, October 8 (Lecture #13)
[Nederhof (1996); Class Notes (Figure PDF)]

Working with Finite-state Automata (Cont'd)
- Application: Building lexicons
  - The simplest types of lexicons are lists of morphemes which, for each morpheme, store the surface form and syntactic / semantic information associated with that morpheme.
  - A list of surface forms can be stored as FSA in two ways:
    - DFA encoding of a trie (= retrieval tree)
    - Deterministic acyclic finite automaton (DAFA)
  - Create a trie by compacting a word-list; create a DAFA for a word-list by compacting a trie-DFA for that word-list.
  - Example #1 (see figure): A trie-DFA and a DAFA encoding the lexicon {"in", "inline", "input", "our", "out", "outline", "output"}.
  - Basic operations on tries
    - Checking if a word is encoded in a trie T:
    - Adding a word to a trie T:
  - All known algorithms for creating tries and DAFA run in low-order polynomial time (and access to individual words can be done in time linear in the size of the word of interest, regardless of the size of the trie or DAFA); however, tries and minimized DAFA can be too large for computer memory for even moderate-size applications.
    - Solution: incremental algorithms (on sorted / unsorted word-lists) which simultaneously create and minimize DAFA as they add words one at a time! (Daciuk et al (2000))
    - Incremental algorithms are not quite the fastest known algs but they are close; moreover, given their minimal memory requirements, are the most practical. (Daciuk (2002))
  - The information associated with a surface form is most easily encoded in an FSA by encoding access to that information in the final state associated with that form in the FSA.
    - While this can be very compact (particularly if DAFA are used to encode surface forms), can be problematic if the number of possible forms of this associated information is not a small finite set, e.g., syntactic-role vs. semantic info.
    - In those cases, more complex schemes may be desirable, e.g., index-generating DAFA (Lucchesi and Kowaltowski (1992); see also Grana et al (2001) and references), FST that operate over surface-form / associated information string-pairs (Mohri (1996); Mihov and Maurel (2000)).
- Application: Implementing simple morphotactics
  - More complex lexicons need to take into account how morphemes are combined to form words.
  - The simplest types of purely concatenative morphotactics can be encoded as a finite-state manner by indicating for each morpheme-type sublexicon which types of morphemes can precede and follow morphemes in that sublexicon, e.g., nouns precede pluralization-morphemes in English.
    - Can be simplified to specifying continuation classes for a sublexicon L, i.e., those sublexicons whose morphemes can validly occur in a word after morphemes in L.
    - The morphotactics of such a language can then be viewed as FSA with in which nodes correspond to sublexicons and continuation-classes are encoded as epsilon-transitions between the appropriate pairs of sublexicon-nodes.
  - A more straightforward implementation is to encode sublexicons as trie-FSA or DAFA as described above and encode continuation classes using concatenation. Separate concatenated chains of sublexicons can then be combined using union.
    - As union and concatenation can be done in time and space linear in the sizes of the argument FSA, this provides a very time-efficient method for implementing morphotactics and constructing basic word lexicons.
    - However, given memory constraints and the storage requirements of even moderate-size lexicons, consider building lexicons in a piecewise fashion using appropriate concatenation and union operations and minimizing the intermediate lexicons as they are created.
  - More complex morphotactics, e.g., circumfixes, infixes, reduplication, can be layered on top of lexicon FST using additional FST-based mechanisms (Beesley and Karttunen (2000); Beesley and Karttunen (2003), Chapter 8; Kiraz (2000)).
  - Though the finite-state framework is a tad constricting in places (especially wrt the auxiliary information that can be easily associated with a lexical form), it does provide a unified and standard methodology for creating and using lexicons. Moreover, it also provides easy integration of lexicons with other finite-state implementable applications (see below).
- Application: Implementing simple constraint-based systems
  - Simple constraints, i.e., those operating overs strings, can be implemented as FSA, and the intersection of the constraints in such a system can be simulated using the FSA created by the sequential intersection of the FSA corresponding to the constraints.
  - Simple though this may seem, one should beware cascading FSA intersections! Intersecting k |Q|-state FSA operating over a common alphabet Sigma requires O(|Sigma||Q|^{2k}) time and space by the pairwise intersection algorithm described above and there is strong evidence that there is no significantly faster algorithm (Finite State Automata Intersection is PSPACE-complete (Garey and Johnson (1979), Problem AL6, p. 266))
Working with Finite-state Transducers
- Implementing basic operations
  - Checking acceptance of a string-pair l/u by a FST F:
    - Adapt the string-recognition algorithm for FSA given above.
    - If F is an l/u-deterministic FST, the algorithm above runs in O(max(|l|,|u|)) time and space; otherwise, the algorithm runs in O(|Q|^{max(|l|,|u|)}) time and O(max(|l|,|u|)) space, where |Q| is the number of states in F.
  - Reconstructing the string associated with a given string by a FST F:
    - Adapt the string-pair recognition algorithm for FST given above. Consider here the case where the given string is l in string-pair l/u and we are reconstructing u.
      An analogous algorithm reconstructs the lower string associated with a given upper string.
    - Note that the algorithm above reconstructs all strings associated with a given string; in NLP applications, this is particularly important when reconstructing the possible underlying lexical forms associated with a given surface form.
    - If F is an l/u-deterministic FST, the algorithm above runs in O(max(|l|,|u|)) time and space; otherwise, the algorithm runs in O(|Q|^{max(|l|,|u|)}) time and O(max(|l|,|u|)) space, where |Q| is the number of states in F.

Friday, October 10 (Lecture #14)
[Nederhof (1996); Class Notes (Figure PDF)]

Working with Finite-state Transducers
- Implementing basic operations (Cont'd)
  - Focus on FST combination operations that are closed, i.e., operations on one or more FST that yield another FST.
  - Let F1 and F2 be two FST which recognize the sets of string-pair sets S1 and S2, respectively, and assume without loss of generality that all strings in S1 and S2 are over a common alphabet Sigma. Let us consider several operations that combine F1 and F2 to create an FST FR.
  - Composition of F1 and F2 (Kaplan and Kay (1994), pp. 341-342; Kaplan and Kay (1996))
    - FR recognizes all string-pairs x:y such that x:z is in S1 and z:y is in S2 for some string z.
    - Create FR as follows:
      - For each state q1 in F1 and and q2 in F2, add state (q1,q2) to FR.
      - Add the following transitions to FR:
        
        ((q1,q2),x:y,(q3,q4)) such that there are transitions (q1,x:z,q3) in F1 and (q2,z:y,q4) in F2, where z can be any symbol (including epsilon));
        ((q1,q2),x:epsilon,(q3,q2)) such that there are transitions (q1,x:epsilon,q3) in F1 and (q2,z:y,q4) in F2 where z is not epsilon; and
        ((q1,q2),epsilon:y,(q1,q4)) such that there are transitions (q1,x:z,q3) in F1 and (q2,epsilon:y,q4) in F2 where z is not epsilon.
    - Note that the start state of FR is (qs1,qs2) and the final states of FR are all states (q1,q2) such that q1 is a final state in F1 and q2 is a final state in F2.
    - The FST FR above essentially simulates the operation of F1 and F2 in parallel, and does away with the need for separate storage for the intermediate result that is the output of F1 and the input of F2.
    - Example #1 (see figure): The FST created by composing the following two FST in this order: (1) an FST for transforming all occurrences of "aab" to "aac", and (2) an FST implementing a vowel-harmony-like process, in which all c's (b's) following an initial b (c) are transformed into b's (c's).

Week 7 [Class Notes]

Monday, October 13

Midterm break; no lecture

Wednesday, October 15 (Lecture #15)
[Nederhof (1996); Class Notes (Figure PDF)]

Working with Finite-state Transducers
- Implementing basic operations (Cont'd)
  - Composition of F1 and F2 (Kaplan and Kay (1994), pp. 341-342; Kaplan and Kay (1996)) (Cont'd)
    - Example #1 (see figure): The FST created by composing the following two FST in this order: (1) an FST for transforming all occurrences of "aab" to "aac", and (2) an FST implementing a vowel-harmony-like process, in which all c's (b's) following an initial b (c) are transformed into b's (c's) (Cont'd)
    - Example #2 (see figure): The FST created by composing the FST in Example #1 in the opposite order.
    - Example #3: The FST created by composing two FST that implement the following rules: (1) voice must be added to the noun-final plural morpheme /s/ if the last sound in the noun is voiced and (2) an extra vowel be added before the plural morpheme if the last sound in the noun is [sh] or [zh], e.g., dishes, buzzes.
      - Note that FST #1 in this example is based on the FST given in Example #3 in Lecture #10, but is modified to retain the plural-morpheme marker. This is done so that FST #2 above may use this marker to correctly place the extra vowel before that plural morpheme when the final sound in the noun is [sh] or [zh].
    - If F1 and F2 have |Q1| and |Q2| states, respectively, FR is a |Q1||Q2| state FST that is created in O(|Sigma|(|Q1||Q2|)^2) time and space.
  - Intersection of F1 and F2
    - FR recognizes all string-pairs x:y such that x:y is in S1 and S2.
    - FR can be created using the algorithm for pairwise FSA intersection described above, modified to require transition symbol-pair rather than just transition-symbol identity.
    - Must be careful, as intersection of arbitrary FST can produce non-finite-state recognition power, e.g., the intersection of FST recognizing (c^n, a^* b^n) and (c^n, a^n b^*) is an FST recognizing (ac^n, a^n b^n) whose upper language is context-free (Kaplan and Kay (1994), p. 342).
      - For this reason, intersection is often restricted to FST that encode restricted classes of string-pair sets such as the same-length relations, i.e., string-pair sets such that for each member x:y, |x| = |y| (Kaplan and Kay (1994), Section 3.3).
  - Various other operations on FST are known and defined, e.g., union, complementation, repetition, reversal, subtraction, and all run in low-order polynomial time and space; however, some operations are only defined relative to particular subclasses of FST (Kaplan and Kay (1994), Section 3).
- Application: Implementing rule- and complex constraint-based systems
  - Complex constraints, i.e., those operating overs string-pairs, can be implemented as FST encoding same-length relations, and the simultaneous intersection of constraints can be simulated using the FST created by the sequential intersection (in an arbitrary order) of the FST corresponding to the constraints.
    - See Section 7 of Kaplan and Kay (1994) for a detailed description of how this is done for one of the most popular complex constraint-based systems implementing morphonology, Two-Level Morphology.
  - In a similar manner, many types of linguistic rules can be implemented as FST, and the sequential application of rules can be simulated using the FST created by the sequential composition (in the specified order) of the FST corresponding to the constraints.
    - See Sections 4 and 5 of Kaplan and Kay (1994) for a detailed description of how this is done for one of the most popular rule-based systems implementing phonology, namely, that described in Chomsky and Halle's 1968 book The Sound Pattern of English (known as the SPE Model).
  - Simple though this may seem, one should again beware, this time of cascading FST intersections or compositions! Intersecting and composing k |Q|-state FST requires O(|Sigma||Q|^{2k}) time and space by the pairwise intersection and composition algorithms described above and there is strong evidence that there are no significantly faster algorithms (Same-length FST Intersection is NP-hard (Barton, Berwick and Ristad (1987), Chapter 5; Wareham (1999), Section 4.4.2; Wareham (2002), Theorem 10); Same-length FST Composition is NP-hard (Wareham (1999), Section 4.3.2; Wareham (2002), Theorem 12)).
- Application: Implementing lexical transducers (Beesley and Karttunen (2003), Section 1.8)
  - A lexicon FSA can be converted into an FST by replacing each transition-label x with x:x, e.g., the identity FST associated an FSA. This lexicon FST can then be composed wit the the underlying / surface transformation FST encoding a constraint- or rule-based morphonological system to create a lexical transducer.
    - Note as FST are bidirectional, so are lexical transducers; hence, can reconstruct surface or lexical forms from given lexical or surface forms with equal ease.
    - Creating this lexical transducer (and applying determinization and minimization algorithms to it) will take exponential time and space in the worst case; however, once it is done, surface and lexical forms can be processed very efficiently (in time linear in the length of the given surface or lexical form).
  - Analysis of lexicon-encoded known forms
    - Run lexical transducer in reverse on surface form to derive associated lexical form.
    - If there are several language-variants, can run surface form against each of the associated lexical transducers until one succeeds.
  - Analysis of lexicon-encoded known forms + unknown forms
    - Unknown forms are typically those in which a root unknown to the lexicon has been acted on by lexicon-encoded morphotactics, e.g., loanwords, words that have been back-formed from other words (television => televise).
    - Create "guesser" transducer which encodes standard morphotactics but in which root forms are replaced by a sub-transducer that recognizes all phonologically-possible roots in the language on the surface side and adds a special lexical tag, e.g., +guess, on the lexical side.
    - If a given surface form is not recognized by the known-form lexical transducer, run it against the guesser transducer to extract potential roots; these can then be presented to the user for validation and possible addition (via union) to the known-form lexical transducer.

Friday, October 17

Lecture cancelled.

Week 8 [Class Notes]

Monday, October 20 (Lecture #16)
[BKL, Chapter 8; J&M, Chapter 13; Class Notes (Figure PDF)]

Working with Context-free Grammars (BKL, Chapter 8; J&M, Chapters 13 and 14)
- Though there are context-free morphophonological phenomena, context-free grammars are primarily used to both recognize and parse sentences relative to a syntactic grammar.
  - Parsing both recognizes and adds an internal structure to a sentence; in the case of syntactic parsing, this structure is the hierarchical constituent phrase-structure of the sentence.
  - As mentioned previously, this phrase-structure is useful as a model of the semantics of a sentence.
- Parsing a sentence S with n words relative to a grammar G can be seen as a search over all possible derivation trees that can be generated by grammar G with the goal of finding all derivation trees whose leaves are labelled with exactly the words in S in an order that (depending on the language, is either exactly or is consistent with) that in S.
- Parsing algorithms can be classified using two dimensions:
  - Type of search
    - Dictated by the source of constraints on the search.
    - Top-down (goal-directed) search is constrained by the derivation-trees consistent with the given grammar G; bottom-up (data-directed) search is constrained by the words in given sentence S and their order within that sentence.
    - Top-down search will only consider derivation-trees consistent with G, but may end up generating derivation-trees that are not consistent with S; bottom-up search will only consider derivation-tree structure consistent with S, but may end up generating local derivation-tree sub-structures that are not consistent with G.
    - Example #1 (see figure): Example of derivation trees generated by top-down search for the sentence "Book that flight" (J&M, Figure 13.3).
    - Example #2 (see figure): Example of derivation trees generated by bottom-up search for the sentence "Book that flight" (J&M, Figure 13.4).
  - Mechanisms of search
    - Types of mechanisms used in parsing algorithm to implement (and possibly speed up) search.
    - Naive implementations of search use backtracking, which is simple and space-efficient but runs the risk of generating derivation tree substructures multiple times.
    - Smarter implementations of search use dynamic programming, which remembers intermediate derivation-tree substructures so they are not generated multiple times but can be complex and much more costly wrt space.
- Though some algorithms implement the generation of one valid parse for a given sentence much quicker than others, the generation of all valid search trees (which is required in the simplest human-guided schemes for resolving sentence ambiguities) for all parsing algorithms is in the worst case at least the number of valid derivation-trees for the given sentence S relative to the given grammar G.
  - There are natural grammars for which this is quantity is exponential in the number of words in the given sentence (BKL, p. 317; Carpenter (2003), Section 9.4.2).
- Implementing deterministic context-free parsing
  - Recursive-descent parsing [top-down / backtracking] (BKL, pp. 303-304; Carpenter (2003), Section 9.4.4)
    - Grows a derivation-tree downward, starting from a tree consisting of a single node labelled with grammar-sentence / start symbol S and, at each point, generating daughter-derivation trees by expanding leftmost leaf-node labelled with a non-terminal in all possible ways that this non-terminal can be expanded by the grammar.
      - Note that leftmost non-terminal leaf-node expansion corresponds to depth-first derivation-tree generation.
    - Every time a derivation-tree is created with n leaves, it is checked to see if these leaves (if terminal) or direct expansion of these leaves into words (if non-terminal) results in the given sentence. If so, that derivation-tree is valid for the sentence. Otherwise, backtracking is invoked to try another possible tree.
    - Example #3 (see figure): Example of recursive-descent parse for for the sentence "The dog saw the man in the park" (BKL, Figure 8.4).
    - In the worst case, this algorithm requires O(|#DT(G,n)||LDT(G,n)|) time and O(n|LDT(G,n)) space to generate either one or all valid parses of a given sentence, where |#DT(G,n)|$ is the number of derivation-trees with n leaves consistent with grammar G and |LDT(G,n)| is the maximum possible size of derivation-tree with n leaves that is consistent with G.
    - Though simple and having a low space complexity, this algorithm has all the problems associated with the top-down parsing approach. The depth-first search version described here has the additional problem that left-recursive rules, e.g., NP -> NP PP, can make the algorithm go into an infinite loop.
      - This last problem can be fixed by either removing rules of this form (conversion to Greibach Normal Form (HU79, Section 4.6)) or pre-processing the grammar to extract constraints that can be used in a hybrid top-down / bottom-up manner (left-corner parsing (BKL, 306-307; Carroll (2003), Section 12.3.2)).

Wednesday, October 22 (Lecture #17)
[BKL, Chapter 8; J&M, Chapter 13; Class Notes (Figure PDF)]

Working with Context-free Grammars (BKL, Chapter 8; J&M, Chapters 13 and 14) (Cont'd)
- Implementing deterministic context-free parsing (Cont'd)
  - Shift-reduce parsing [bottom-up] (BKL, pp. 304-306)
    - Grows a derivation-tree upwards from the left-hand side of a sentence using a stack initialized to empty and two operators:
      - Shift: Place the next word to be processed in the given sentence on the stack.
      - Reduce: Replace the topmost k, k >= 1, entities y1, y2, ..., yk on the stack with the higher-level non-terminal X if there is a rule of the form X -> y1 y2 ... yk in the given grammar G.
      The process terminates when no shift or reduce operations can be applied, and recognizes the given sentence as valid relative to G if only the grammar sentence / start symbol S is all that remains on the stack.
    - Example #4 (see figure PDF): Example of shift-reduce parse for for the sentence "The dog saw the man in the park" (BKL, Figure 8.5).
    - In the worst case, this algorithm requires O(|LDT(G,n)|) time and space to generate one valid parse of a given sentence.
    - Though simple and having a low space complexity, this algorithm has all the problems associated with the bottom-up parsing approach. The simple version described above has the additional problem that it is incorrect, in that it may fail to find a valid parse even when one exists.
      - This last problem occurs because there may a choice of operators to apply at any point (some but possibly not all leading to alternate valid parses caused by ambiguity).
      - These problems can be resolved by adding backtracking, though this may dramatically raise the time and space complexity.
      - For unambiguous well-structured grammars, choosing operators using both stack and bounded lookahead in the portion of the given sentence yet to be processed may suffice to guarantee correctness; indeed, it is this strategy that is used in many parsers for computer programming languages!
  - A Brief Interlude: Dynamic Programming
    - Applies if a problem has a recursive decomposition in which the number of distinct subproblems is bounded and can be organized in an n-dimensional table.
    - Characteristics of recursive decomposition:
      - Can decompose instance of problem into smaller instance of the same problem, i.e., subproblems.
      - At any point in the computation, may be several choices for decomposition.
      Problems that are solvable by recursive decomposition have the optimal substructure property, i.e, an optimal solution for an instance of the problem can be constructed using optimal solutions for instances of that problem that are of smaller size (subproblems).
    - Example:: Computing Fibonacci numbers
      - Recurrence
      - Recursive algorithm:
        
        FibR(n) if ((n == 1) || (n == 2)) return(1) else return(FibR(n - 1) + FibR(n - 2))
      - Recursive-calls tree: 2^{n/2} - 1 <= Tree Size <= 2^{n} - 1
      - The problem here is that subproblems are being repeated; perhaps the recursive algorithm can keep track of what subproblems have been solved by storing those values in a table and look these up as necessary? An algorithm that does this is called a memoized algorithm.
      - Memoized (recursive) algorithm:
        
        InitFibT(n,FibT) Allocate n-element table and assign to FibT FibT[1] = FibT[2] = 1 for (i = 3; i <= n; i++) FibT[i] = INFINITY FibM(n, FibT) if (FibT[n] == INFINITY) FibT[n] = FibM(n - 1, FibT) + FibM(n - 2, FibT) return(FibT[n])
      - This table idea was pretty neat. In fact, do we really need the recursion anymore? Let's just fill out the table!
      - Dynamic programming (iterative) algorithm:
        
        FibI(n) if ((n == 1) || (n== 2)) return(1) else Allocate n-element table FibT FibT[1] = FibT[2] = 1 for (i = 3; i <= n; i++) FibT[i] = FibT[i - 1] + FibT[i - 2] return(FibT[n])
    - If we are lucky, there are a polynomial number of distinct subproblems. If we are really lucky, we can use the recurrence to solve these subproblems in a "bottom up" rather than a "top down fashion", solving the smallest subproblems first and solving progressively larger subproblems until we solve the original problem instance.
    - Dynamic programming (DP) => table-driven, bottom-up recursive decomposition algorithms!
    - The Dynamic Programming Cookbook:
      - Step 1: Find a recurrence / recursive decomposition for the problem of interest.
      - Step 2: Lay out the distinct subproblems in a table.
      - Step 3: Fill in the base-case values in the table.
      - Step 4: Run the recurrence "in reverse" / in a bottom-up fashion, using smaller solved subproblems to solve larger subproblems, until the table is filled in.
      - Step 5: Use traceback from the optimal-cost table entry, e.g., FibT[n], to reconstruct one or more optimal solutions for the problem.
  - The Cocke-Kasami-Younger (CKY) algorithm [bottom-up / dynamic programming] (BKL, pp. 307-310; J&M, Section 13.4.1)
    - Given an n-word sentence, place n+1 markers labelled 0, 1, ..., n such that marker 0 is before the first word, marker 1 is between the first and second words, and so on.
    - Observe that as the constituents in a derivation tree are hierarchically nested, each constituent "covers" the words between some pair of markers i and j where 0 <= i < j <= n; moreover, the daughter constituents of each constituent (as determined by the application of some rule in the given grammar G) together completely cover the words between markers i and j.
    - The above implies that the set of all possible constituents in a derivation-tree for a given n-word sentence can be viewed as a set of subproblems p[i,j], 0 <= i < j <= n, where p[i,j] is the set of possible top-constituents in a valid parse of the words between markers i and j.
    - These subproblems can be organized into the upper-right triangular submatrix of an (n+1) x (n+1) matrix P in which the row-index i starts at 0 in upper-left corner and increases going down and the column-index j starts at 0 in the upper-left corner and increases going left to right.
      - The first diagonal of P (entries of the form (i,i+1), 0 <= i < n) correspond to the individual words in S, and P[i,i+1] is initialized to the possible non-terminals for word i+1 in S.
      - The set of all possible daughter-constituents of a constituent in P[i,j] is in the "ragged boomerang of table-cells in P behind and below P[i,j].
    - Can fill in P going from left to right, ascending each column; save traceback information to reconstruct derivation-trees in the entries in the NT back-pointer arrays stored in each entry in P.
    - If at the end of this fill-in procedure P[0][n].NT["S"] is nonempty then there is a valid parse of the given sentence relative to G, and this derivation-tree can be reconstructed using the traceback information.

Thursday, October 23

In-class Exam #2 Notes
I've finished making up the second in-class exam. The exam will be closed-book. It will be 50 minutes long and has a total of 50 marks (this is not coincidental; I have tried to make the number of marks for a question approximately equivalent to the number of minutes it should take you to do it). The exam will cover material in from Lecture # 9 up to and including Lecture # 18. There will be three questions:
- Finite-state automata (3 parts / 28 marks total)
- Finite-state transducers (3 parts / 10 marks total)
- Context-free Grammars (2 parts / 12 marks)
I hope the above helps, and I wish you all the best of luck with this exam.

Friday, October 24 (Lecture #18)
[BKL, Chapter 8; J&M, Chapter 13; Class Notes (Figure PDF)]

Working with Context-free Grammars (BKL, Chapter 8; J&M, Chapters 13 and 14) (Cont'd)
- Implementing deterministic context-free parsing (Cont'd)
  - The Cocke-Kasami-Younger (CKY) algorithm [bottom-up / dynamic programming] (BKL, pp. 307-310; J&M, Section 13.4.1) (Cont'd)
    - Example #1 (see figure): Example of CKY parse for for the sentence "Book the flight through Houston" (adapted from J&M, Figures 13.9 and 13.12).
    - Algorithm Version #1 (basic version for grammars in Chomsky--Normal Form (CNF), i.e., rules of the form N -> N' N'' and N' -> t):
    - Time complexity of matrix fill-in: (# table entries) x (#choices per table entry) x (max # subproblems per choice) = (n(n - 1)/2) x O(n) x O(1) = O(n^3).
    - Space complexity: (# table entries) x (size per table entry) = (n(n - 1)/2) x (|G| x n) = O(|G|n^3)
    - There is an easy procedure for converting an arbitrary content-free grammar to CNF (J&M, pp. 437-438). However, it is not really necessary (or desirable) to get rid of unary non-terminal transformation rules, i.e., N -> N', so it would be nice to modify the algorithm above to handle them directly.
    - Algorithm Version #2 (modified to allow extended CNF with unary non-terminal transformation rules):
    - Time complexity of matrix fill-in: (# table entries) x (#choices per table entry) x ((max # subproblems per choice) + (processing-cost for unary rules)) = (n(n - 1)/2) x (O(n) x (O(1) + O(|G|^2))) = O(n^3|G^2|).
    - Space complexity: (# table entries) x (size per table entry) = (n(n - 1)/2) x (|G| x n) = O(|G|n^3)

Week 9 [Class Notes]

Monday, October 27

In-class Exam #2

Wednesday, October 29 (Lecture #19)
[J&M, Chapter 14; Class Notes (Figure PDF)]

Working with Context-free Grammars (BKL, Chapter 8; J&M, Chapters 13 and 14) (Cont'd)
- Implementing deterministic context-free parsing (Cont'd)
  - The Cocke-Kasami-Younger (CKY) algorithm [bottom-up / dynamic programming] (BKL, pp. 307-310; J&M, Section 13.4.1) (Cont'd)
    - Note that the algorithms given in the previous lecture only fill in the table. There is a relatively simple procedure for retrieving all of the valid derivation-trees from the stored traceback information; however, its running time is lower-bounded by the possible number of such trees, which we know is lower-bounded in the worst case by a function exponential in n.
    - It is possible to accommodate more general types of context-free grammars than extended CNF, and from the viewpoint of linguists using the output of parsers, that would be very desirable. This could be done by either modifying the output of CKY to reconstruct derivation-trees relative to the original non-CNF grammars or by modifying CKY to handle these more complex grammars; however, both approaches, though implementable, are complex.
  - The Earley algorithm [top-down / dynamic programming] (J&M, Section 13.4.2)
    - This algorithm re-uses the inter-word marker system described above for the CKY algorithm and constructs an (n+1)-entry table where entry i, 0 <= i <= n, contains descriptions of possible partial parses consistent with the grammar for a sequence of words ending at marker i.
    - Though complex in structure, this algorithm runs O(n^3) time and space for arbitrary context-free grammars and runs even faster for specific types of grammars, e.g., linear time for unambiguous grammars.
      - Unlike the basic recursive-descent algorithm, the Earley algorithm performs better if the given algorithm is left-recursive!
- Though the worst-case complexity results above favor the dynamic-programming-based algorithms, they may not be the best choice in all situations. Testing (Carpenter (2003), Section 9.8) has shown that search-based methods like recursive-descent and shift-reduce are much better than dynamic-programming algorithms (in particular, CKY) if input sentences are short, given grammars have little ambiguity, and available memory storage is at a premium; the situation reverses if given grammars are more ambiguous and memory is not an issue.
- In any case, dealing with very large numbers of output derivation-trees is problematic. What can be done?

Friday, October 31 (Lecture #20)
[J&M, Chapter 14; Class Notes (Figure PDF)]

Working with Context-free Grammars (BKL, Chapter 8; J&M, Chapters 13 and 14) (Cont'd)
- Implementing probabilistic context-free parsing (J&M, Chapter 14)
  - Solve problem of multiple derivation-trees by only computing the derivation-tree with highest probability for the given utterance!
  - Consider first the straightforward model of probabilistic context-free grammars (PCFG) described previously in Lecture #11, in which probabilities are added to rules such that for each non-terminal, the sum of the probabilities of all rules with that terminal as the left-hand-side is 1.
    - This implies that a rule has the same probability, regardless of where that rule applies in the derivation-tree, e.g., an NP -> Det N is an NP -> Det N is an NP -> Det N ...
    - This also applies to rules that expand lowest-level non-terminals into words, e.g., a Prep -> "in" is a Prep -> "in" is a Prep -> "in" ...
  - Relative to PCFG, the probability of a derivation-tree for a sentence is computing by multiplying together all of the probabilities of the rules used to create that tree (or alternatively, the probabilities of each constituent in the tree, as each constituent is the result of applying a particular rule).
    - But don't the rules of probability say that in order for this computation to be valid, the rules must apply independently of each other? Yes they do. The extent to which this true (especially in light of the two interesting properties of PCFG noted above) will be important later.
  - The Probabilistic CKY algorithm (J&M, Section 14.2)
    - One of the main ways that the probabilistic CKY algorithm differs from its deterministic counterpart is that instead of storing each table entry all possible ways in which a given constituent can be produced in each cell, it only stores the way which has the highest associated probability.
    - Algorithm Version #1 (basic version for grammars in CNF):
    - The time and space complexities of this algorithm are the same as for Version #1 of deterministic CKY given in the previous lecture, namely, O(n^3) and O(|G|n^3), respectively.
    - Algorithm Version #2 (modified to allow extended CNF with unary non-terminal transformation rules):
    - The time and space complexities of this algorithm are the same as for Version #1 of deterministic CKY given in the previous lecture, namely, O(n^3|G^2|) and O(|G|n^3), respectively.
    - Problems can arise dealing with the very small quantities resulting from repeated multiplying of low probabilities. However, this can be accommodated by using the logarithms of these probabilities and adding (instead of multiplying) these logarithmic quantities.
      - Note that even after taking logarithms, the higher probabilities still have higher values, e.g., if p(x) = 1/4 > 1/8 = p(y) then it is still the case that log2(p(x)) = -2 > -3 = log2(p(y)).
    - Algorithm Version #3 (modified to allow extended CNF with unary non-terminal transformation rules and logarithmic probabilities):
    - The time and space complexities of this algorithm are the same as for Version #2 above.
    - Note that the three algorithms above only fill in the table. However, as there is only a single derivation tree (namely, the most probable one), the recursive reconstruction procedure is even simpler than the one for deterministic CKY and runs in O(|G|n) time and space.
  - One can easily create PCFG versions of other deterministic parsing algorithms (for example, a probabilistic version of the Earley algorithm is popular in the NLTK package). However, all of these versions (including Probabilistic CKY described above) suffer from two problems (J&M, Section 14.4):
    - Rules manipulating only non-terminals are not independent, i.e., the same such rule can have different probabilities in different parts of a sentence. For example, it is known from statistical analyses of actual utterances that the frequencies of expansions of noun-phrases as pronouns or non-pronouns depend on whether or not the noun phrase is the subject or object in the sentence (J&M, p. 468):
    - Rules transforming non-terminals into words are not independent, i.e., the same such rule can have different probabilities in different parts of a sentence. For example, the frequency of P -> "in" in actual utterances can vary dramatically depending on where the associated prepositional phrase occurs (see Example #1 in the figure-file for this lecture (J&M, Figure 14.7)).
      - The situation in this figure is actually much worse than it first appears -- even though the left-hand parse tree is valid and the right-[hand one is invalid, as they invoke the same rules (albeit in a different order), the two trees have the same probability.
  - The first of these problems can be solved by modifying the grammar to include variants of the same non-terminal that depend on context, e.g., NP is split into subjectNP and objectNP (J&M, Section 14.5). However, the most commonly adopted solution is to use more complex models of probabilistic context-tree grammars than PCFG, e.g., probabilistic lexicalized CFGs, and parsers specific to those models, e.g., the Collins parser (J&M, Section 14.6; M&S, Chapter 12).
  - All of the above has highlighted the advantages and difficulties of working with probabilistic context-free grammars. However it has deftly avoided a rather crucial issue:
    We will defer answering this question several weeks, to when we look at the broader issue of linguistic knowledge acquisition in both human beings and NLP systems.

Week 10 [Class Notes]

Monday, November 3 (Lecture #21)
[Class Notes (Figure PDF)]

Working with Finite-state Machines Redux
- Implementing probabilistic finite-state machines
  - Recall that probabilistic FSM are automata or transducers with probabilities associated with each transition such that for each state, the sum of the probabilities of all transitions leaving that state is 1.
  - Probabilistic FSM are typically implemented relative to a more general form known as weighted FSM (see Mohri et al (2000) and Pereira and Riley (1997) and references))
    - The theory of weighted FSM has a vast associated literature going back 50 years.
    - The weights on the transitions of the FSM are actually the elements of a semiring, and in addition to probabilities can be other entities such as integers, real numbers, strings or regular expressions (Mohri et al (2000), Sections 2 and 3.1).
    - All operations on FSM have corresponding analogues relative to weighted FSM; however, the algorithms are often more complex and and may even be unrelated to the algorithms for those operations on classical FSM (Mohri et al (2000), Section 3.1).
      - Many of the weighted FSM operation algorithms use generalized shortest-path algorithms. In those cases, it is often convenient to re-code probabilities as their negative logarithms such that most-probable paths correspond to shortest (or rather, minimum summed-weight) paths.
      - Given the ludicrous sizes of the WFSM typically created in NLP applications, many of these operation algorithms have versions that only construct portions of WFSM as they are needed, e.g., lazy WFST composition (Mohri et al (2000), Sections 3.3 and 3.4; see also Pereira and Riley (1997), Section 15.2.4).
      - Optimized versions of all of these algorithms are available in software packages such as OpenFST.
  - Finding the most probable path for a given string in a PFSA or a string-pair in a PFST is done using the Viterbi algorithm (Vidal et al (2005a), Section 3.2; Vidal et al (2005b), Section 4.1), which runs in low-order polynomial time and space.
  - Finding the most probable reconstruction for a given string in a PFSA is NP-hard in general; however, in the cases of deterministic or unambiguous PFST, this can be done using a Viterbi-like algorithm in low-order polynomial time and space (Vidal et al (2005b), Section 4.1).
  - As we will see later, despite such algorithms, it may still be worthwhile to rephrase computations on PFSM in terms of WFSM.
- A related type of probabilistic finite-state mechanism is Hidden Markov Models (HMM) (J&M, Sections 6.1-6.5).
  - In Markov models, it is the states (or rather, the labels assigned to states) that matter -- transitions only have associated probabilities.
  - A Markov model describes the probabilities of sequences of states occurring in a process, e.g., changing weather (J&M, Section 6.1). This is encoded by specifying the transition probabilities between a set of labeled states.
  - Example #1 (see figure): Markov models for changing weather and the words in an utterance (J&M, Figure 6.1).
  - A Hidden Markov Model assumes that state labels are not directly accessible but are rather indirectly indicated by another set of observations, e.g., inferring the weather from observations of the number of ice creams purchased per day (J&M, Section 6.2). This is encoded by adding probabilities of the various observations to each state.
  - Example #2 (see figure): A hidden Markov model relating number of ice creams purchased to the weather (J&M, Figure 6.3).
  - There are many algorithms for manipulating HMM (J&M, Sections 6.3-6.5).
- HMM have many important applications within NLP; however, they can be easily accommodated within the WFSM framework given the trivial manner in which HMM can be converted to PFSA (Vidal et al (2005b), Section 2.3; Dupont et al (2005)). Over the next few lectures, we will encounter several NLP applications where this is a good idea.

Wednesday, November 5

Instructor (was) sick; lecture cancelled.

Friday, November 7 (Lecture #22)
[Class Notes]

Applications: Automated Speech Recognition and Generation (J&M, Sections 8 and 9; Dutoit and Stylianou (2003); Lamel and Gauvin (2003))

Automated Speech Recognition (ASR) (J&M, Chapter 10; Lamel and Gauvin (2003))

Focuses on recovering the individual words in a speech signal; if is augmented to recover meaning of sentences and larger units of discourse, is called Automated Speech Understanding (ASU).
Used in human-computer interaction (e.g., telephony) and dictation.
Difficulty of ASR varies along several dimensions:
- Small vs. large vocabulary to be recognized.
- Isolated-word vs. continuous (read) vs. continuous (conversational) speech.
- Quiet vs. noisy speech environment.
- Standard / trained-on pronunciation vs. accented / dialect pronunciation.

Base word recognition error rates as of 2006 (J&M, Table 9.1):

Task	Vocabulary	Error Rate (%)
TI Digits	11	0.5
Wall Street Journal read speech	5,000	0.3
Wall Street Journal read speech	20,000	3
Broadcast news	64,000+	10
Conversational Telephone Speech (CTS)	64,000+	20

These rates are currently decreasing by about 10% every year due to algorithmic and hardware improvements (J&M, p. 287); however, other factors can still dramatically increase errors rates over and above those in the table (e.g., 3-4x by strong accent and 2-4x with noisy environment).

The current goal is to get good Large-Vocabulary Continuous Speech Recognition (LVCSR).
The most commonly-used ASR framework for the last 40 years is probabilistic inference combined with information theory.
- The Noisy Channel model underlying this framework assumes that if one can accurately construct a model of the noisy channel over which the speech signal is being sent, then one can reconstruct the words associated a speech signal by running possible sequences of words S through the channel model and then comparing each such output with O to find the most probable match.
- This is stated mathematically as P(S|O) = argmax_{S} P(O|S)P(S), where P(O|S) is the acoustic model (speech -> phones) and P(S) is the language model (phones -> (sequences of) words).
- Acoustic models may be stated relative to units smaller or larger than phones (Lamel and Gauvin (2003), p. 310); however, phone-based models have the advantage that they are explicitly linked to and can build on existing linguistic knowledge.
- Note that language models must also segment speech into words, as (unlike text) it may be very difficult to accurately locate the gaps between words in certain speech signals, e.g., fast conversational speech in a noisy environment.
Three phases in probabilistic ASR:
- Sample and encode speech signal.
- Run encoded speech sample-sequence through acoustic model to infer most probable phone-sequence.
- Run inferred phone-sequence through language model to infer most probable word-sequence.
The speech signal is typically sampled every 10-20ms and each sample is encoded with a standard set of 39 features summarizing the signal spectrum in terms of present sound frequencies in the human hearing range (100 - 20,000 Hz) and energies at those frequencies.
As the speech signal associated with a phone typically changes over the duration of that phone, each phone in the acoustic model is encoded as a 3-state HMM (for the start, middle, and end phase of the phone) where samples can loop back on the individual states to allow for variation in phone-phase durations.
Language models are created using a word-pronunciation dictionary and a model of how words are typically ordered in sentences. The pronunciation dictionary is used to create an HMM for each word in that dictionary using the HMM for individual phones in the acoustic model, and these word-HMM are combined into a larger HMM that takes sentence word-order into account.
- Word-order is typically modeled probabilistically by 3- or 4-gram statistics over words in sentences; however, in certain restricted ASR domains, probabilistic finite-state grammars may be used instead.
The fused acoustic-language model HMM is run against the encoded speech sample-sequence to get the most probable associated sequence of words using the Viterbi algorithm.
- Even though the basic Viterbi algorithm runs in low-order polynomial time, the enormous size of a typical fused acoustic-language model HMM makes heuristics necessary, e.g., pruning, beam search.
- Such heuristics mean that produced word-sequences are not guaranteed to be the most probable all inputs.

All of the above is impressive; however, note that many of the traditional phonological and morphological processes operating between individual phones and sequences of words that have been hypothesized and studied by linguists are absent. Indeed, valuable information such as prosody is deliberately filtered out and ignored in the focus on individual phones, which (given the semantic- and discourse-level importance of such information) is seen as a major shortcoming of current ASR systems (Baker et al (2009b), p. 78).
Automated Speech Generation (ASG) (J&M, Chapter 9; Dutoit and Stylianou (2003))
- ASG is actually the oldest of all NLP techniques, having first been done by purely mechanical means simulating the action of the human vocal tract in the late 1700's.
- Used in human-computer interaction (e.g., telephony, artificial voices for the disabled (Stephen Hawking)).
  - Though ASG can transform from either a lexical representation or written text to a speech signal, ASG is often also known as Text-to-Speech Synthesis (TTS).
- The two phases of ASG are (1) transformation of given text to an intermediate phonemic representation (text analysis) and (2) transformation of the intermediate phonemic representation to the speech signal (waveform synthesis).
  - If the text is written text, additional pre-processing is necessary to expand non-standard words such as symbols and abbreviations in the text to standard words, infer sentence boundaries, and disambiguate homographs (words of different meaning that are written the same), e.g., "use" (verb) vs. "use" (noun).
- The majority of the words in most texts are readily transformed to phonemic representations using pronunciation dictionaries. However, several problems remain:
  - Upwards of 5% of words in written text are not in standard pronunciation dictionaries (e.g., names, foreign words or phrases); and
  - Standard pronunciation dictionaries often do not include syllabifications for words or other word-internal prosody details, let alone phrase- or sentence-level prosody information.
  The first problem is typically dealt with using grapheme-to-phoneme rules (g2p). There are various mechanisms for reconstructing word-internal prosody that are reasonably accurate; however, phrase- or sentence-level prosody (which often depends on semantics and discourse) is very difficult to reconstruct accurately (J&M, p. 271). For this reason, most prosody is reconstructed to mimic neutral declarative (i.e., Prozac / lobotomized) speech.
- Waveform synthesis can be done in three ways:
  - Simulate human vocal tract producing phonemes (articulatory synthesis);
  - Simulate abstract sound-frequency characteristics of phonemes (formant synthesis); or
  - Concatenate appropriate units of stored speech (with modifications for prosody as necessary) (concatenative synthesis).
  Concatenative synthesis is the most popularly-used technique, and is typically done relative to either diphones (which cover the middle of one phone to the middle of the next phone, to accommodate phone co-articulation effects) or arbitrary-length units (which accommodate word co-articulation effects).
Most if not all of the HMM and rule-based tasks invoked above can be re-phrased in terms of various operations on and the composition of weighted finite-state accepters and transducers (Pereira and Riley (1997); Mohri, Pereira, and Riley (2002)). This not only gives a uniform framework for expressing and implementing ASR and ASG systems, but it also allows these systems to exploit standard techniques such as lazy composition for speeding up and minimizing the memory used by WFSM-based systems.
One nagging question remains: Where are all the probabilities being invoked in the various HMM and probabilistic rule-based transformations coming from? The answer to this question is linked to the other major factor in improvements in ASR and ASG over the last few decades, namely, the increasing availability of ever larger and more comprehensive databases of speech and text (Baker et al (2009), p. 75). Precisely how this helps will be examined when we look at issues of artificial language acquisition one week from now.

Week 11 [Class Notes]

Monday, November 10 (Lecture #23)
[Class Notes (Figure PDF)]

Applications: Morphological and Syntactic Parsing
- As we have seen in previous lectures, if one excludes exotic phenomena like reduplication, morphological parsing of words can be done using deterministic finite-state mechanisms. Similarly, syntactic parsing of utterances can be done using deterministic and probabilistic context-free mechanisms.
- There a variety of forms of partial ("shallow") morphological and syntactic parsing which are desirable in particular applications.
- Stemmers and Lemmatizers (Sub-word Morphological Parsing) (BKL, Section 3.6; J&M, Section 3.8)
  - Given a word, a stemmer removes known morphological affixes to give a basic word stem, e.g., foxes, deconstructivism, uncool => fox, construct, cool; given a word which may have multiple forms, a lemmatizer gives the canonical / basic form of that word, e.g., sing, sang, sung => sing.
  - Stemmers and lemmatizers are used to "normalize" texts as a prelude to selecting content words for a text or selecting general word-forms for searches, e.g., process, processes, processing => process, in information retrieval.
  - Stemmers typically apply morphology in reverse without regard for meaning, and hence have quick-running finite-state implementations, e.g., the Porter stemmer (J&M, Section 3.8); though they also exploit reverse morphology and can be implemented in part using finite-state mechanisms, lemmatizers are slower as they also need to consult lexicons.
  - There are a variety of stemmers implementing different degrees of affix removal and hence different levels of generalization. It is important to chose the right stemmer for an applications, e.g., if "stocks" and "stockings" are both stemmed to "stock", financial and footwear queries will return the same answers.
- Part-of-Speech (POS) Tagging (Single-level Syntactic Parsing) (BKL, Chapter 5; J&M, Chapter 5)
  - Given a word in an utterance, a POS tagger returns a guess for the POS of that word relative to a fixed set of POS tags.
  - The output of POS taggers are used as inputs to other partial parsing algorithms (see below), automated speech generation (to help determine pronunciation, e.g., "use" (noun) vs. "use" (verb)), and various information retrieval algorithms (see below) (to help locate important noun or verb content words).
  - There a number of POS algorithms:
    - Determine tag by presence or absence of specific morphological affixes.
    - Determine tag by consulting lexicon.
    - Determine tag by making default initial guess and then revising guesses as necessary using fixed-context transformation rules (transformation-based / Brill tagging).
    - Determine most probable tag using n-gram statistics.
    - Determine most probable tag using a HMM.
    These algorithms have differing performances, knowledge-base requirements, and running times and space requirements. Hence, no POS tagger is good in all applications.
- Chunking (Few-level Syntactic Parsing) (BKL, Chapter 7; J&M, Section 13.5)
  - Given an utterance, a chunker returns a non-overlapping (but not necessarily total in terms of word coverage) breakdown of that utterance into a sequence of one or more basic phrases or chunks, e.g., "book the flight through Houston" => [NP(the flight), PN(Houston)].
  - A chunk typically corresponds to a very low-level syntactic phrase such as a non-recursive NP, VP, or PP.
  - Chunkers are used to isolate entities and relationships in texts as a pre-processing step for information retrieval.
  - FST-based algorithms undo non-recursive grammar rules to produce sequence of tags denoting chunks as well as words outside chunks.
  - HMM-based algorithms use IOB tagging to implicitly denote chunks in terms of the word-tags I (internal to chunk), O (outside chunk), and B (beginning of chunk).
- Shallow Parsing (Multi-level Syntactic Parsing) (Abney (1996); J&M, Section 13.5.1)
  - Given an utterance, a shallow parser gives an (often flattened) approximation of the full parse generated by a context-free parser.
  - When implemented using composed cascades of chunker FSTs implementing progressively higher-level finite-state approximations to context-free syntax rules, a shallow parser can provide a more efficient alternative to full CFG parsing.
  - Example #1 (see figure): A chunking-FST cascade implementing a shallow parse of the utterance "the morning flight from Denver has arrived" (J&M, Figure 13.18).

Tuesday, November 11

Course Project Talk and Paper Notes
I have finished marking the Course Project Proposals. I have done up a schedule for talks associated with each proposal that will run in extended 75 to 90 minute versions of our lecture slots starting on Monday, November 24, and concluding on Wednesday, December 3. The talks are ordered in a pseudo-random fashion, with talks on related topics grouped on the same day where possible to encourage further discussion. I realize that some of you have other classes at 1pm on lecture days; in those cases, please arrange to switch your talks with other people talking the same day as you and, when this is done, tell me the changes so I can adjust the on-line schedule accordingly.
Each one-, two-, and, three-person talk is alloted 15, 20, and 25 minutes, respectively. Five minutes of each talk at the end will for questions, and multi-person talks are expected to divide the remaining time up approximately equally between the people involved. You may use the in-class blackboard and AV facilities as you please during your talks. You may also structure your talks as you please; a general guideline would be to not try to cram all the details of the paper you are writing into the talk but rather to give an introductory "advertisement" stressing (as in your Course Proposals) why your topic is interesting and previous work on that topic.
Your Course Project paper is due by midnight on Wednesday, December 3; please e-mail the PDF file of your paper to me. The paper should be between 12 and 20 double-spaced pages including 10 and 30 references (in the case of literature-survey projects) and five to eight double-spaced pages including 10 to 15 references (in the case of software projects). All included references MUST be cited in the main text or footnotes of the paper. Though purely Web-based references (e.g., blogs, reference manuals) are acceptable, please try where at all possible to obtain literature-based references, e.g., books, book chapters, journal papers, conference papers; in those cases, give full references listing all reference information appropriate to the type of reference, author names, publication year, full paper title, book title with editors, journal name, journal volume and number, publisher, page numbers.
Here's to each of you having fun working on your course project!

Wednesday, November 12 (Lecture #24)
[Class Notes]

Applications: Language Understanding (Utterance) (BKL, Section 10; J&M, Section 17)
- When considering an utterance in isolation from its surrounding discourse, the goal is to infer a semantic representation of the utterance giving the literal meaning of the utterance, e.g., "I think it's lovely that your mother is staying with us for a month."
- Five computationally desirable characteristics for a semantic representation formalism (J&M, Section 17.1):
  - The meaning encoded in a representation can be (preferably efficiently but at the very least in principle) verified wrt the real world.
  - The meaning encoded in a representation is unambiguous, i.e., a representation cannot encode two meanings.
  - Inputs having the same meaning have the same representation (canonical form).
  - Representations of meaning support both inference and variables.
  - The formalism is expressive enough to encode all required meanings.
  Note that the last two characteristics must be stated relative to a particular application and semantic domain.
- A commonly-used representation that satisfies most of the above requirements for many simple applications is First-Order Logic (FOL) (propositional logic augmented with predicates and (possibly embedded) quantification over sets of one or more variables), e.g.,
  - "Everybody loves somebody sometime." ->
    FORALL(x) person(x) => EXISTS(y,t) (person(y) and time(t) and loves(x, y, t))
  - "Every restaurant has a menu" ->
    FORALL(x) restaurant(x) => EXISTS(y) (menu(y) and hasMenu(x,y)) [All restaurants have menus]
  - "Every restaurant has a menu" ->
    EXISTS(y) and FORALL(x) (restaurant(x) => hasMenu(x,y)) hasMenu(x,y)) [Every restaurant has the same menu]
- The simplest utterance meanings can be built up from the meanings of their various syntactic constituents, down to the level of words (Principle of Compositionality (Frege)).
  - In this view, individual words have meanings which are stored in the lexicon, and these basic meanings are composed and built upon by the relations encoded in the syntactic constituents of the parse of the utterance until the full meaning is associated with the topmost "S"-constituent in the parse.
  - Each grammar rule thus also has an associated semantics-augmentation which constructs the meaning of the LHS non -terminal from the meanings of the RHS non-terminals (The Rule-to-Rule Hypothesis (Bach)).
- Such compositional semantics can either be done after parsing relative to the derivation-tree or during parsing in an integrated fashion (J&M, Section 18.5). The latter can be efficient for unambiguous grammars, but otherwise runs the risk of expending needless effort building semantic representations for syntactic structures considered during parsing that are not possible in a derivation-tree.
  - Given the unambiguous nature of programming language grammars, the integrated approach can be and is used to efficiently assign semantics to programs during compilation or interpretation; in yet another parallel development, these techniques were developed in program translation theory in Computer Science independently of semantic theory in NLP.
- Though powerful, there are many shortcomings of this approach, e.g.,
  - Even in the absence of lexical and grammatical ambiguity, ambiguity in meaning can arise from ambiguous quantifier scoping, e.g., the two possible interpretations above of "every restaurant has a menu" (J&M, Section 18.3).
  - The meanings of certain phrases and utterances in natural language are not compositional, e.g., "roll of the dice", "grand slam", "I could eat a horse" (J&M, Section 18.6)
  Many of these shortcomings can be mitigated using more complex representations and representation-manipulation mechanisms; however, given the additional processing costs associated with these more complex schemes, the best ways of encoding and manipulating the semantics of utterances is still a very active area of research.

Thursday, October 13

In-class Exam #3 Notes
I've finished making up the third in-class exam. The exam will be closed-book. It will be 50 minutes long and has a total of 50 marks (this is not coincidental; I have tried to make the number of marks for a question approximately equivalent to the number of minutes it should take you to do it). The exam will cover material in from Lecture # 17 up to and including Lecture # 27. There will be two questions:
- Deterministic and Probabilistic Context-free Grammar Parsing (3 parts / 28 marks)
- NLP Applications (4 parts / 22 marks)
I hope the above helps, and I wish you all the best of luck with this exam.

Friday, November 14 (Lecture #25)
[Class Notes (Figure PDF)]

There are two types of multi-utterance discourses: monologues (a narrative on some topic presented by a single speaker) and dialogues (a narrative on some topic involving two or more speakers). As the NLP techniques used to handle these types of discourse are very different, we shall treat them separately.
Applications: Language Understanding (Discourse / Monologue) (J&M, Chapter 21)
- The individual utterances in a monologue are woven together by two types of mechanisms:
  - Coherence: This encompasses various types of relations between utterances showing how they contribute to a common topic, e.g. (J&M, Examples 21.4 and 21.5),
    - John hid Bill's car keys. He was drunk.
    - John hid Bill's car keys. He hates spinach.
    as well as use of sentence-forms that establish a common entity-focus, e.g. (J&M, Examples 21.6 and 21.7),
    - John went to his favorite musical store to buy a piano. He had frequented the store for many years. He was excited that he could finally buy a piano. He arrived just as the store was closing for the day.
    - John went to his favorite music store to buy a piano. It was a store that John had frequented for many years. He was excited that he could finally buy a piano. It was closing just as John arrived.
  - Coreference: This encompasses various means by which entities previously mentioned in the monologue are referenced again (often in shortened form), e.g., pronouns (see examples above).
- Ideally, reconstructing the full meaning of a monologue requires correct recognition of all coherence and coreference relations in that monologue (creating a monologue parse graph, if you will). This is exceptionally difficult to do as the low-level indicators of coherence and coreference (for example, cue phrases (e.g., "because" "although") and pronouns, respectively) have multiple possible uses and are thus ambiguous, and resolving this ambiguity accurately can be either very computationally costly or even impossible.
- Computational implementations of coherence and coreference recognition are often forced to rely on heuristics, e.g., using on recency of mention and basic number / gender agreement to resolve plurals (Hobb's Algorithm: J&M, Section 21.6.1).
  - These heuristics are often based on characterizations of human discourse created by linguists and psychologists, and hence have the flavor of ad hoc recipes or lists rather than deep universally-applicable knowledge.
  - Then again, maybe this is how humans process discourse ...
- Alternatively, one can weaken one's notion of what the meaning of a monologue is:
  - Summarize the overall meaning of a monologue as a vector of relevant words or phrases, where relevance is easily computable, e.g., words or phrases that are repeated frequently in the monologue (but not too frequently ("the")).
  - Summarize the most "important" meaning of a monologue in terms of the key entities in the monologue and their relations to each other, e.g., who did what to who in that news story?
  There are a very large number of weak NLP techniques used to access these types of monologue meaning; they are the subject of study in the subdisciplines of Information Retrieval (Tzoukermann et al (2003); J&M, Section 23.1) and Information Extraction (BKL, Chapter 7; Grishman (2003); J&M, Chapter 22) respectively.
Applications: Language Understanding (Discourse / Dialogue) (J&M, Chapters 23 and 24)
- Even if one participant plays a more prominent role in terms of the amount speech or guiding the ongoing narrative, every dialogue is at heart a joint activity among the participants.
- Characteristics of dialogue (J&M, Section 24.1):
  - Participants take turns speaking.
  - There may be one or more goals (initiatives) in the dialogue, each specific to one or more participants.
  - Each turn can be viewed as a speech act that furthers the goals of the dialogue in some fashion, e.g., assertion, directive, committal, expression, declaration (J&M, p. 816).
  - Participants base the dialogue on a common understanding, and part of the dialogue will be assertions or questions about or confirmations concerning that common understanding.
  - Both intention and information may be implicit in the utterances and must be inferred (conversational implicatures), e.g., "You can do that if you want" (but you shouldn't), "Sylvia does look good in that dress" (and why did you notice?).
- Example #1 (see figure): Architecture of a Speech Dialogue System (SDS) (J&M, Figure 24.5).
- The core of an SDS is the Dialogue Manager (DM). An ideal DM should be able to accurately discern both explicit and implicit intentions and information in a dialogue, model and reason about both the common ground and the other participants in the dialogue, and take turns in the dialogue appropriately. This is exceptionally difficult to do, in large part because the domain knowledge and inference abilities required verge on those for full AI-style planning, which are known to be computationally very expensive (J&M, Section 24.7).
- Implemented SDS deal with this by restricting their functionality and domain of interaction and retaining the primary initiative in the dialogue while allowing limited initiative on the part of human users, e.g., travel management and planing SDS (J&M, pp. 811-813).
  - The simplest single-initiative DM have finite-state implementations (Example #2 (see figure) (J&M, Figure 24.9)); more complex mixed-initiative DM structure dialogues in terms of semantic frames whose slots can be filled in a user-directed order.
  - In addition to simplifying the DM, the restrictions above can also dramatically simplify the required language understanding and generation abilities to handle only expected interaction-types (J&M, p. 822).
  - Basic SDS can be built using dialogue-specification programming languages such as VoiceXML (J&M, Section 24.3).
  - HMM-based DM are possible, but require (a to-date seldom attainable degree of) accurate common-ground and user-intention modeling (J&M, Section 24.6).

Week 12 [Class Notes]

Monday, November 17 (Lecture #26)
[Class Notes]

Applications: Language Understanding (Discourse / Dialogue) (J&M, Chapters 23 and 24) (Cont'd)
- Alternatively, SDS can focus on maintaining the illusion of dialogue while having the minimum (or even no) underlying mechanisms for modeling common ground or dialogue narrative:
  - Question Answering (QA) Systems (Harabagiou and Moldovan (2003); J&M, Chapter 23)
    - Such systems answer questions from users which require single-word or phrase answers (factoids).
    - Given the limited form of most questions, the topic of a question can typically be extracted from the question-utterance by very simple parsing (sometimes even by pattern matching).
    - Factoids can then be extracted from relevant texts, where relevance is assessed using techniques from Information Retrieval and Information Extraction. Given the computational expense of applying even efficient heuristics over a large number of texts, this is typically done in a two-phase process in which very cheap heuristics are used to isolate a small set of potentially relevant text, which are then processed in more detail by more expensive methods (J&M, p. 779).
  - Chatbots
    - Such systems engage in conversation with human beings, sometimes with some explicit purpose in mind (e.g., telephone call routing (Lloyds Banking Group, Royal Bank of Scotland, Renault Citroen)) but more often just as entertainment.
    - The first chatbots were ELIZA (Weizenbaum (1966): a simulation of a Rogerian psychotherapist) and PARRY (Colby (1981): a simulation of a paranoid personality).
      - ELIZA maintains no conversational state, instead relying on strategic pattern-matching of key phrases in user utterances and substitution of these phrases in randomly-selected utterance-frames. PARRY maintains a minimal internal state corresponding to the degree of the system's own "emotional agitation", which is then used to modify selected user utterance-phrases and their response-frames.
    - There are many chatbots today, e.g.,
      (see also The Personality Forge and The Chatterbot Collection); however, they all rely on modifications of the mechanisms pioneered in ELIZA and PARRY.
    - Regardless of the simplicity of the mechanisms involved, chatbots can (with the co-operation of the human beings that they interact with) give a startling illusion of sentience (Epstein (2007); Weizenbaum (1967, 1979)). This is due in large part to innate human abilities to extract order from the environment, e.g., hearing voices or seeing faces in random audio and visual noise, which (in the context of interaction) assumes sentience and agency where none is present, e.g., "Because Zog was struck by lightning after he dug the well, the Mighty and Unknowable Spirit of An-hur obviously does not want us to dig any more wells."
- Current dialogue systems can give impressive illusions of understanding and do indeed have sentient ghosts within them -- however, for now, these ghosts come from us.
Applications: Automated Language Acquisition
- Initial results in formal language learning and subsequent results in computational learning theory (see Clark and Lappin (2011) and references) suggest that it is computationally very difficult and in cases even provably impossible to acquire various types of languages. Those schemes that do work also require very large numbers of valid utterances and on occasion large pools of invalid examples (the latter being particularly useful in preventing the inference of overly general languages and/or grammars).
- These results are at odds with the characteristics of human language acquisition (see Lecture # 7) which demonstrate that human beings acquire language efficiently with relatively few valid examples and no (or at least very few) invalid examples (Poverty of the Stimulus (POS))
- This has lead to two schools of thought within the language acquisition community in linguistics:
  - Nativist (Internal-Driven): Human beings are born with a Universal Grammar (UG) such that, on minimal exposure to actual utterances from a particular language, that language can be efficiently acquired by inferring the appropriate settings of parameters in the UG.
  - Empiricist (Data-Driven): Human beings are born with powerful general-purpose inference abilities (e.g., probabilistic or analogical inference) which, in conjunction with restrictions in the structure of human languages (and, in some cases, minimal-grammar assumptions), allow the efficient acquisition of languages.
  The extreme versions of each school can be seen as the endpoints of a continuum, and it is generally acknowledged that the mechanisms underlying actual language acquisition probably lie somewhere in the middle.
- These schools within linguistics have corresponding schools within the NLP language acquisition community, with the nativist school relying on hand-derived categories and grammars derived from linguistics and the empiricist school relying powerful statistical and machine learning algorithms (BKL, Chapters 6 and 9; J&M, Chapter 6; Manning and Schutze (1999)).
  - Though the pure Nativist NLP approach is tedious to implement, it has the advantage that morphosyntactic mechanisms incorporate semantic categories and thus interface seamlessly with semantic, discourse, and pragmatics processing systems.
  - The pure Empiricist NLP approach has been very successful in automatically inferring phonetic, phonological, morphological, and syntactic mechanisms. However, the basic supervised learning algorithms used to date require extremely large annotated databases of actual utterances which, while increasingly available (BKL, Chapter 11; J&M, Section 12.4), are difficult to produce. Moreover, as such databases tend to be confined to non-semantic domains, inferred categories and grammars may not be semantically meaningful and hence cannot easily interface with semantic, discourse, and pragmatics processing systems.
- It seems likely that once the Empiricist NLP community integrates insights derived within the Empiricist linguistic community (in particular, the exploitation of restrictions in the structure of human languages and minimal-grammar assumptions), further dramatic progress will be made. However, for the moment, NLP systems cannot automatically acquire the full range of human linguistic knowledge.

Wednesday, November 19 (Lecture #27)
[Class Notes (Figure PDF)]

Applications: Spelling Checking and Correction
- Characteristics of word misspelling
  - Based on four types of errors: single symbol insertion / deletion / substitution or adjacent symbol transposition (Damerau (1964)).
  - Vast majority of misspellings involve only one error, e.g., roughly 2% of unknown words in a corpus are due to multiple-error misspellings (Ren and Perrault (1992), cited on page 253 of Savary (2002)).
  - The number of possible correct words increases dramatically as number of possible errors increases, e.g., O(n^k) possible corrections for a word of length n created by k errors.
- Two types of spelling-related tasks:
  - Spell checking: determine whether or not a given word is misspelled.
  - Spelling correction: create a list of candidate correct words for a given misspelled word; choice of correction is then left to the user.
- Spell checking can be done by reconstruction relative to a lexical transducer; if the given word as surface form does not have an associated lexical form, that word is misspelled.
- The simplest scheme for spelling correction envisions each possible type of error as an optional rewrite rule; the transducers associated with these rules are composed with the surface-form automaton associated with a standard lexical transducer, and a given word is associated with all words that can be created from it by any sequence of errors (Section 9.6, Beesley and Karttunen (2003)).
  - This is a straightforward, purely finite-state implementation of Damerau (1964).
  - There are several major difficulties with this approach -- namely, ordering the rewrite rules to take into account even the most elementary multi-error misspellings is difficult, and returned candidates are not ordered in any sensible way, e.g., by number / probability of errors invoked.
- More complex schemes explicitly compute and rank candidates related by multiple spelling errors; to do this, three things must be specified:
  - A measure of spelling error distance between two words, e.g., Levenshtein / edit and weighted edit distance (see Section 4 of Kruskal (1984) and references), error distance (Du and Chang (1992)).
  - Degree of maximum allowable spelling error (distance threshold).
  - Type of correction list ((ordered) exhaustive vs. nearest neighbor).
    - Nearest neighbor approaches suffice in many applications, as long lists of candidates are both hard to compute and discouraging for users to sort through (Savary (2002), p. 253).
- Sample algorithms:
  - Oflazer (1996) [error distance / arbitrary threshold / exhaustive]
  - Mihov and Schulz (2004) [Levenshtein / edit distance / arbitrary threshold / exhaustive]
  - Savary (2002) [error distance / arbitrary threshold / nearest neighbor]
  All of these algorithms employ depth-first search on lexical transducer, with various types of mechanisms for pruning relative to cut-off error distance.
- Oddly enough, there is a parallel and independent algorithmic tradition for this problem within formal language theory, e.g., Myers and Miller (1989) [Levenshtein / edit distance / -- / nearest neighbor], Kari et al (2003) [weighted edit distance / -- / nearest neighbor]!
  - Though such algorithms support arbitrary distance thresholds, the increase in candidate-set size with threshold typically limits thresholds to values less than 4 in practice; however, given the statistical rarity of multi-error misspellings, this is frequently sufficient.
- Despite all the algorithmic sophistication above, given the incompleteness of encoded lexicons, decisions about whether an unknown form is a new word to be added to the lexicon or a misspelled form of a known word cannot (and maybe should not) be completely automated, e.g., is "blints" a misspelling of "blink" [Plural], the plural of a new word "blint", or a previously unencoded term for a traditional Jewish cheese-stuffed pancake?
  - Indeed, the ability of NLP systems to reliably recognize whether or not a word is knew is listed as one of the grand challengers of ASR in particular and NLP in general (Baker et al (2009a), p. 77).
Applications: Machine Translation (MT) (Hutchins (2003); J&M, Chapter 25; Somers (2003))
- MT was among the first applications studied in NLP (J&M, p. 905). MT (and indeed, translation in general) is difficult because of various deep morphosyntactic and lexical differences among human languages, e.g., wall (English) vs. wand / mauer (German) (J&M, Section 25.1).
- Three classical approaches to MT (J&M, Section 25.2):
  - Direct: A first pass on the given utterance directly translates words with the aid of a bilingual dictionary, followed by a second pass in which various simple word re-ordering rules are applied to create the translation.
  - Transfer: A syntactic parse of the given utterance is modified to create a partial parse for the translation, which is then (with the aid of a bilingual word and phrase dictionary) further modified to create the translation. More accurate translation is possible if the parse of the given utterance is augmented with basic semantic information.
  - Interlingua: The given utterance undergoes full morphosyntactic and semantic analysis to create a purely semantic form, which is then processed in reverse relative to the target language to create the translation.
  The relations between these three approaches are often summarized in the Vauquois Triangle (Example #1: See figure (J&M, Figure 25.3)).
- The Direct and Transfer approaches require detailed (albeit shallow) processing mechanisms for each pair of source and target languages, and are hence best suited for one-one or one-many translation applications, e.g., maintaining Canadian government documents in both English and French, translating English technical manuals for world distribution. The Interlingua approach is best suited for many-many translation applications, e.g., inter-translating documents among all 25 member states of the European Union.
- In part because of the lack of progress, the Automated Language Processing Advisory Committee (ALPAC) report recommended termination of MT funding in the 1960's. Research resumed in the late 1970's, re-invigorated in large part because of advances in semantics processing in AI as well as probabilistic techniques borrowed from ASR (J&M, p. 905).
- Statistical MT re-uses the Noisy Channel model from ASR, this time construing inference over probabilistic translation and language models cf. acoustic and language models in ASR.
  - The translation models assess the probability of a given utterance being paired with a particular translation using the concept of word/phrase alignment.
  - Example #2 (see figure): An alignment of the English utterance "And the letter was sent Tuesday." and the corresponding French translation"Le lettre a ete envoyee le mardi." (J&M, Figure 25.19).
  - To create the necessary probabilities (which are typically encoded in HMM), need large large databases of valid (often manually created) alignments.
- Fully Automatic High-Quality Translation (FAQHT) is the ultimate goal. This currently achievable for translations relative to restricted domains, e.g., weather forecasts, basic conversational phrases. Current MT (which is largely based on the statistical approach) is acceptable in larger domains if rough translations are acceptable, e.g., as quick-and-dirty first drafts for human subsequent human editing (Computer-Aided Translation (CAT)). (J&M, pp. 861-862; see also BBC News (2014)). It seems likely that further improvements will require a fusion of classical (in particular Interlingua) and statistical approaches.

Friday, November 21

In-class Exam #3

Week 13 [Class Notes]

Monday, November 24

Course Project Presentations (Day 1)
- Adam Murphy: Meme Processing (15 minutes)
- Scott Young: Irony Processing (15 minutes)
- Andrew DeRoche: Exploiting Punctuation (15 minutes)
- Jeremy Woolley: Text Simplification (15 minutes)
- Mike Singleton: Data Structures for Lexicons (15 minutes)

Wednesday, November 26

Course Project Presentations (Day 2)
- Darwin Carrillo: Q/A Systems in Education (15 minutes)
- Dongkang Li: Chatbot Technologies (15 minutes)
- Ryan Murphy: Cognition-inspired PDA NLP (15 minutes)
- Ryan Martin: Data Structures for Lexicons (15 minutes)
- Niall Delaney: Text Classification (15 minutes)

Friday, November 28

Course Project Presentations (Day 3)
- Wei Wei: Word Segmentation in Chinese (15 minutes)
- Chaoyuan Chen: Chinese-based Machine Translation (15 minutes)
- Lauren Mallaly: Models of Machine Translation (15 minutes)
- Mark Stacey: Internet Text Processing (15 minutes)

Week 14 [Class Notes]

Monday, December 1

Course Project Presentations (Day 4)
- Tim Murray: Discourse Context Processing (15 minutes)
- Ali Alfosool and Bukunola Ladele: Multilingual ASR Accuracy (20 minutes)
- Jordan Porter, Joshua Rodgers, and Matthew Newell: Commercial ASR Algorithms (25 minutes)
- Olanrewaju Okunloala: User Modeling for NLP (15 minutes)
- Jarret Kolanko: Finite-state Spelling Correction (15 minutes)

Wednesday, December 3

Course Project Presentations (Day 5)
- Allan Collins: Special-purpose Hardware for NLP (15 minutes)
- Stephen Brinson: NLP in Interactive Fiction Games (15 minutes)
- Zack Mullaly: Functional Programming in NLP (15 minutes)
- Noah Fleming: Parameterized Complexity of Phrase Alignment (15 minutes)

References

Abney, S.P. (1996) "Partial parsing via finite-state cascades." Natural Language Engineering, 2(4), 337-344.
BBC News (2014) "Translation tech helps firms talk business round the world." (URL: Retrieved November 14, 2014)
Baker, J.M., Deng, L., Glass, J., Khuanpur, S., Lee, C.-H., Morgan, N., and O'Shaughnessy, D. (2009a) "Research Developments and Directions in Speech Recognition and Understanding, Part 1." IEEE Signal Processing Magazine, 26(3), 75-80.
Baker, J.M., Deng, L., Khuanpur, S., Lee, C.-H., Glass, J., Morgan, N., and O'Shaughnessy, D. (2009b) "Research Developments and Directions in Speech Recognition and Understanding, Part 2." IEEE Signal Processing Magazine, 26(6), 78-85.
Barton, G.E., Berwick, R.C., and Ristad, E.S. (1987) Computational Complexity and Natural Language. MIT Press.
Beesley, K.R. and and Karttunen, L. (2000) "Finite-state Non-concatenative Morphotactics." In SIGPHON 2000. 1-12. [PDF]
Beesley, K.R. and and Karttunen, L. (2003) Finite-State Morphology. CSLI Publications.
Bird, S. (2003) "Phonology." In R. Mitkov (ed.) (2003), pp. 3-24.
Bird, S., Klein, E., and Loper, E. (2009) Natural Language Processing with Python. O'Reilly Media. [Abbreviated above as BKL]
Carpenter, B. (2003) "Complexity." In R. Mitkov (ed.) (2003), pp. 178-200.
Carroll, J. (2003) "Parsing." In R. Mitkov (ed.) (2003), pp. 233-248.
Clark, A. and Lappin, S. (2011) Linguistic Nativism and the Poverty of the Stimulus. Blackwell.
Colby, K.M. (1981) "Modeling a paranoid mind." Behavioral and Brain Sciences, 4(4), 515-534.
Daciuk, J. (2002) "Comparison of Construction Algorithms for Minimal Acyclic, Deterministic, Finite-State Automata from Sets of Strings." In CIAA 2002. Lecture Notes in Computer Science no. 2608. Springer-Verlag; Berlin. 255-261. [PDF]
Daciuk, J., Mihov, S., Watson, B.W., and Watson, R.E. (2000) "Incremental Construction of Acyclic Finite-State Automata." Computational Linguistics, 26(1), 3-16.
Damerau, F.J. (1964) "A Technique for Computer Detection and Correction of Spelling Errors." Communications of the ACM, 7(3), 171-176.
Demers, R.A. and Farmer, A.K. (1991) A Linguistic Workbook (2nd Edition). The MIT Press.
Du, M.W. and Chang, S.C. (1992) "A model and a fast algorithm for multiple errors spelling correction." Acta Informatica, 29, 281-302.
Dupont, P., Denis, F., and Esposito, Y. (2005) "Links between probabilistic automata and hidden Markov models: probability distributions, learning models, and induction algorithms." Pattern Recognition, 38, 1349-1371.
Dutoit, T. and Stylianou, Y. (2003) "Text-to-Speech Synthesis." In R. Mitkov (ed.) (2003), pp. 323-338.
Epstein, R. (2007) From Russia With Love: How I got fooled (and somewhat humiliated) by a computer." Scientific American Mind, October, 6-17.
Gazdar, G. and Pullum, G.K. (1985) "Computationally Relevant Properties of Natural Languages and Their Grammars." Next Generation Computing, 3, 273-306. [PDF]
Grana, J., Barcala, M., and Alonso, M.A. (2001) "Compilation Methods of Minimal Acyclic Finite-State Automata for Large Dictionaries." In CIAA 2001. Lecture Notes in Computer Science no. 2494. Springer-Verlag; Berlin. 135-148. [PDF]
Grishman, R. (2003) "Information Extraction." In R. Mitkov (ed.) (2003), pp. 545-559
Harabagiou, S. and Moldovan, D. (2003) "Question Answering." In R. Mitkov (ed.) (2003), pp. 560-582
Hopcroft, J.E., Motwani, R., and Ullman, J.D. (2001) Introduction to Automata Theory, Languages, and Computation (Second Edition). Addison-Wesley. [Abbreviated above as HMU01]
Hopcroft, J.E. and Ullman, J.D. (1979) Introduction to Automata Theory, Languages, and Computation. Addison-Wesley. [Abbreviated above as HU79]
Hutchins, J. (2003) "Machine Translation: General Overview." In R. Mitkov (ed.) (2003), pp. 501-511.
Indurkhya, N. and Damerau, F.J. (eds.) (2010) Handbook of Natural Language Processing (2nd Edition). Chapman and Hall / CRC.
Jurafsky, D. and Martin, J.H. (2008) Speech and Natural Language Processing (2nd Edition). Prentice-Hall. [Abbreviated above as J&F]
Kaplan, R. (2003) "Syntax." In R. Mitkov (ed.) (2003), pp. 70-90.
Kaplan, R and Kay, M. (1994) "Regular Models of Phonological Rule Systems." Computational Linguistics, 20(3), 331-378. [PDF]
Kaplan, R. and Kay, M. (1996) "Finite-state Methods in Natural Language Processing: Algorithms." Lecture notes. [PDF]
Kari, L., Konstantinidis, S., Perron, S., Wozniak, G., and Xu, J. (2003) "Finite-state error edit-systems and difference measures for languages and words." Technical report 2003-01, Department of Mathematics and Computing Science, Saint Mary's University, Canada.
Kay, M. (2003) "Introduction." In R. Mitkov (ed.) (2003), pp. xvii-xx.
Kenstowicz, M.J. (1994) Phonology in Generative Grammar. Basil Blackwell.
Kiraz, G.A. (2000) "Multi-tiered nonlinear morphology using multitape finite automata: A case study on Syriac and Arabic." Computational Linguistics, 26(1), 77-105. [PDF]
Kruskal, J.B. (1984) "An Overview of Sequence Comparison." In D. Sankoff and J.B. Kruskal (eds.) Time Warps, String Edits, and Macromolecules: The Theory and Practice of Sequence Comparison. Addison-Wesley; Reading, MA. 1-44.
Lamel, L. and Gauvin, J.-L. R. (2003) "Speech Recognition." In R. Mitkov (ed.) (2003), pp. 305-322.
Lappin, S. (2003) "Semantics." In R. Mitkov (ed.) (2003), pp. 91-111.
Leech, G. and Weisser, M. (2003) "Pragmatics and Dialogue." In R. Mitkov (ed.) (2003), pp. 136-156.
Lovins, J.B. (1973) Loanwords and the Phonological Structure of Japanese. PhD thesis, University of Chicago.
Lucchesi, C.L. and Kowaltowski, T. (1993) "Applications of finite automata representing large vocabularies." Software - Practice and Experience, 23(1), 15-20. [PDF]
Manning, C. and Schutze, H. (1999) Foundations of Statistical Natural Language Processing. The MIT Press. [Abbreviated above as M&S]
Martin-Vide, C. (2003) "Formal Grammars and Languages." In R. Mitkov (ed.) (2003), pp. 157-177.
Mihov, S. and Maurel, D. (2000) "Direct Construction of Minimal Acyclic Subsequential Transducers." In CIAA 2000. Lecture Notes in Computer Science no. 2088. Springer-Verlag; Berlin. 217-229.
Mihov, S. and Schulz, K.U.. (2004) "Fast Approximate Search in Large Dictionaries." Computational Linguistics, 30(4), 451-477.
Mitkov, R. (ed.) (2003) The Oxford Handbook of Computational Linguistics. Oxford University Press.
Mitkov, R. (2003a) "Anaphora Resolution." In R. Mitkov (ed.) (2003), pp. 266-283.
Mohri, M. (1996) "On some applications of finite-state automata theory to natural language processing." Natural Language Engineering, 2(1), 61-80.
Mohri, M. (1997) "Finite-state transducers in language and speech processing." Computational Linguistics, 23(2), 269-311. [PDF]
Mohri, M. (2004) "Weighted Finite-State Transducer Algorithms: An Overview." In Formal Languages and Applications. Studies in Fuzziness and Soft Computing no. 148. Physica-Verlag; Berlin. 551-564. [PDF]
Mohri, M., Pereira, F., and Riley, M. (2000) "The Design Principles of a Weighted Finite-State Transducer Library." Theoretical Computer Science, 231, 17-32. [PDF]
Mohri, M., Pereira, F., and Riley, M. (2002) "Weighted Finite-State Transducers in Speech Recognition." Computer Speech & Language, 16(1), 69-88. [PDF]
Myers, E.W. and Miller, W. (1989) "Approximate Matching of Regular Expressions." Bulletin of Mathematical Biology, 51, 5-37.
Nederhof, M.-J. (1996) "Introduction to Finite-State Techniques." Lecture notes. [PDF]
Nederhof, M.-J. (2000) "Practical Experiments with Regular Approximation of Context-Free Languages." Computational Linguistics, 26(1), 17-44. [PDF]
Oflazer, K. (1996) "Error-Tolerant Finite-State Recognition with Applications to Morphological Analysis and Spelling Correction." Computational Linguistics, 22(1), 73-89.
Pereira, F. and Riley, M. (1997) "Speech Recognition by Composition of Weighted Finite-State Automata." In E. Roche and Y. Schabes (eds.) (1997), pp. 431-454.
Ramsay, A. (2003) "Discourse." In R. Mitkov (ed.) (2003), pp. 112-135.
Roche, E. and Schabes, Y. (eds.) (1997) Finite-state Natural Language Processing. The MIT Press.
Roche, E. and Schabes, Y. (1997a) "Introduction." In E. Roche and Y. Schabes (Eds.) (1997), pp. 1-66.
Savary, A. (2002) "Typographical Nearest-Neighbor Search in a Finite-State Lexicon and Its Application to Spelling Correction." In CIAA 2002. Lecture Notes in Computer Science no. 2494. Springer-Verlag; Berlin. 251-260.
Somers, H. (2003) "Machine Translation: Latest Developments." In R. Mitkov (ed.) (2003), pp. 512-528.
Sproat, R. (1992) Morphology and Computation. The MIT Press.
Tomlin, R. (1986) Basic Word Order: Functional Principles. Croom Helm.
Trost, H. (2003) "Morphology." In R. Mitkov (ed.) (2003), pp. 25-47.
Tzoukermann, E., Klavans, J.L., and Strazalkowski, T. (2003) "Information Retrieval." In R. Mitkov (ed.) (2003), pp. 529-544.
Vidal, E., Thollard, F., Higuera, C., Casacuberta, F., and Carrasco, R.C. (2005a) "Probabilistic Finite-State Machines -- Part I." IEEE Transactions on Pattern Analysis and Machine Intelligence, 237(7), 1013-1025.
Vidal, E., Thollard, F., Higuera, C., Casacuberta, F., and Carrasco, R.C. (2005b) "Probabilistic Finite-State Machines -- Part II." IEEE Transactions on Pattern Analysis and Machine Intelligence, 237(7), 1026-1039.
Wareham, T. (1999) Systematic Parameterized Complexity Analysis in Computational Phonology. PhD thesis, Department of Computer Science, University of Victoria.
Wareham, T. (2001) "The Parameterized Complexity of Intersection and Composition Operations on Sets of Finite-State Automata." In CIAA 2000. Lecture Notes in Computer Science no. 2088. Springer-Verlag; Berlin. 302-310. [PDF]
Weizenbaum, J. (1966) "ELIZA -— A computer program for the study of natural language communication between man and machine." Communications of the ACM, 9(1), 36-45.
Weizenbaum, J. (1967) "Contextual understanding by computers." Communications of the ACM, 10(8), 474-480.
Weizenbaum, J. (1979) Computer power and human reason. W.H. Freeman.

	Pronoun	Non-Pronoun
Subject	91%	9%
Object	34%	66%

Computer Science 4750, Fall '14 Course Diary

Copyright 2014 by H.T. Wareham All rights reserved

Wednesday, September 3

Friday, September 5 (Lecture #1) [Class Notes]

Monday, September 8 (Lecture #2) [Class Notes]

Wednesday, September 10 (Lecture #3) [Class Notes]

Friday, September 12 (Lecture #4) [Class Notes]

Monday, September 15 (Lecture #5) [Class Notes]

Wednesday, September 17 (Lecture #6) [Class Notes]

Friday, September 19 (Lecture #7) [Class Notes]

Monday, September 22 (Lecture #8) [Nederhof (1996); Class Notes]

Wednesday, September 24

Thursday, September 25

Friday, September 26 (Lecture #9) [Nederhof (1996); Class Notes (Figure PDF)]

Monday, September 29

Wednesday, October 1 (Lecture #10) [Nederhof (1996); Class Notes (Figure PDF)]

Friday, October 3 (Lecture #11) [Class Notes (Figure PDF)]